1. 引言
1990年,吴望名 [1] 在研究逻辑系统中的蕴涵关系时提出了模糊蕴涵代数(简称FI代数)。FI代数一度引起了同行的广泛关注,如,徐扬 [2]、刘练珍 [3] 研究了格蕴涵代数,讨论了FI代数与MV代数间的关系,邓方安 [4] 在研究FI代数的过程中对模糊蕴涵代数的模糊蕴涵算子从代数学角度做了进一步抽象,提出了
代数。文献 [5] 研究了
代数的子代数、理想与关联理想;文献 [6] 研究了
代数的RC-半群;文献 [7] 引入并讨论了
代数的中间单位的性质。本文提出
代数的拟左(右)陪集的概念,并讨论它的性质。
2.
代数的拟左(右)陪集的性质
定义2.1 [4] 设S是含常元0的集合。若在S中定义二元运算
和
满足以下公理:
,
(F1)
,
(F2)
,
(F3)
则称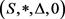 是一个
代数。
是一个
代数。
定理2.1 [4] 若
是
代数,则
,下列等式成立:
(1)
;
(2)
;
(3)
。
推论1 [4] 若
是一个
代数,则
和
都是半群。
因此,
代数是带有一对对偶半群的双半群。
定义2.2 设
是一个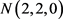 代数,在半群
中定义集合
代数,在半群
中定义集合
.
显然
,即
非空。
,有
,
因此
是S的子代数。
再定义集合
,
分别称为半群
关于子代数
的拟左陪集和拟右陪集。
定理2.2 设
是一个
代数,则半群
的拟左陪集就是半群
的拟右陪集。
证明 由于一个
代数
的半群
与
的特殊关系:
,
,容易得出:半群
的拟左陪集
,
就是半群
的拟右陪集
。
这里只研究拟左陪集,类似可以研究拟右陪集的性质。
在群里,对于任意一个群G,
,则有下列性质成立:
(1)
;
(2)
;
(3)
;
(4) 若
,则有
。
但在
代数
的半群
与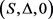 中这些性质不再成立,下面的例子说明了这一点。
中这些性质不再成立,下面的例子说明了这一点。
例1 设
,定义S上的二元运算如下表1,表2:

Table 1. Example of Theorem 2.2(a)
表1. 定理2.2(a)

Table 2. Example of Theorem 2.2(b)
表2. 定理2.2(b)
容易验证:
是一个
代数,且
。而
,
显然
。同时,
,但
。
例2 设
,定义S上的二元运算如下表3,表4:

Table 3. Example of Theorem 2.2(c)
表3. 定理2.2(c)

Table 4. Example of Theorem 2.2(d)
表4. 定理2.2(d)
可以验证:
是一个
代数,且
。而
.
这说明在群里“
”在半群中不再成立。
在群中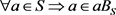 成立,但在半群中,这个结论不一定成立。在上例中,有
,但
。
成立,但在半群中,这个结论不一定成立。在上例中,有
,但
。
定理2.3 设
是一个
代数,则有
。
证明 由
可知,如果
,使得
这与
矛盾,因此
。
定理2.4 设
是一个
代数,则有下列结论成立:
(1)
;
(2)
,如果b是a的右伴随非零零因子,则
;
(3) 若
,且
,则a一定是幂等元;
(4)
,其中
是S的全体幂等元集合。
证明 (1) 设
,因为
是S的子代数,故有
;又任取
,由
,于是
,且
,
从而又得到
。
(2) 设
,令
,
,由b是a的右伴随非零零因子,则有
,
于是一方面
,另一方面
,即
。
(3) 由
知,存在
,使得
(*)
再将
代入(*)式,就有
。
(4)
,故
。
3.
代数与Q-代数、CI-代数及量子B-的关系
定理3.1 若
是一个
代数,
,则在半群
中有下列结论成立:
(1)
;
(2)
。
证明 (1) 由
;
;
(2)
;
,即
是一个右零半群。
定义3.1 [8] 设X是带常元0的一个非空集,在X上定义二元运算
,满足下列公理:
,
(Q1)
;
(Q2)
;
(Q3)
的代数系统
称为Q-代数。
例3 设
,在X上定义二元运算如下表5:
不难验证
是一个Q-代数。
根据
代数的性质和定义2.3易得:
定理3.2 在
代数
中,如果
,则半群
是一个Q-代数。
定义3.2 [9] [10] 设X是带常元0的一个非空集,在X上定义二元运算
,满足下列公理:
,
(CI1)
;
(CI2)
;
(CI3)
的代数系统
称为CI-代数。
例4 设
,在X上定义二元运算如下表6:
可以验证
是一个CI-代数。
由定理2.1容易得到:
定理3.3 在
代数
中,如果
,则有下列结论成立:
(I)
是一个Q-代数;
(II)
是一个CI-代数。
定义3.3 [11] [12] [13] 设X是带有两个二元运算
和
的偏序集,如果满足:
,有
(1)
(2)
(3)
则称
是一个量子B-代数。
定理3.4 设
是一个
代数上定义关系“
”:
或
,
如果
,满足
,则关系“
”是
上的一个偏序,此时
代数
就是一个量子B-代数。
证明:(1) 由
;
(2)
;
即
。
(3) 由
因此,
。
于是关系“
”是
上的一个偏序。
再由在半群
上,
,于是
,
视“
”为“
”,“
”为“
”,则定义2.2中条件(1)成立。
由
,
从而得到:
,
即得到(2)
成立。
,
因此,条件(3)
成立。
基金项目
国家自然科学基金资助项目(61561040)。