1. 引言
关于函数空间上以有界调和函数为符号的Toeplitz算子拟正规性的研究,主要集中在Hardy空间和Bergman空间上。文献 [1] 中给出了Hardy空间上以三角多项式为符号的Toeplitz算子的亚正规性的结果,在2013年,Phukon和Hazarika [2] 刻画了Bergman空间上Toeplitz算子
是亚正规的必要条件。本文思考将某符号的Toeplitz算子亚正规性问题推广到加权Bergman空间上进行研究。
2. 预备知识
在这一部分中,我们介绍了Mellin变换我们将在下一节计算中运用这个公式。
定义1.1 若
是
上的可积函数(即
),可定义Mellin变换
:
.
Mellin变换是半平面
上的有界解析函数。
定义1.2 对于
,
,D上加权Bergman空间
是解析函数空间在
上。此时,
.
显而易见,
是Hilbert空间
中的闭子空间。
定义1.3 设
,若
,称T为正规算子。若满足
,
引理1.1 [3] 若
为
上的有界解析函数,在两两不相同的点列
上取值为零,若
1)
,
2)
,
则
在半平面
上恒等于零。
注解:我们经常用到引理1.1的一种特殊情况:若
为
上的有界解析函数,若存在自然数序列
使得
且
,
则
。
重要的是,一个函数是由Mellin变换的零点决定的。
引理1.2 [4] 设
。如果存在
,
使得
,
则
。
3. 主要结果
引理2.1 [5]
,
,
,
其中
,
那么有对于非负整数n,有
1)
2)
其中
为
的Mellin变换。
定理2.1
,
且
,
。若
为亚正规算子,则
1)
时,
。
2) 时,
。
时,
。
证明:由引理2.1,当
时,
。
又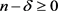 时,
时,
若
,
。
若
,当
时,
。进一步有
,其中,
,
.
选取
,使得f的幂级数展开式中前
项为0,则
由于
, 。那么有
。那么有
.
在
时,故有
.
如此下去,
。
。而
,
,
,故
。
若
,
则
亚正规当且仅当
4. 结论
本文研究了加权Bergman空间上Toeplitz算子
,其中
,且
, ,
为亚正规算子的一个必要条件:
,
为亚正规算子的一个必要条件:
若
为亚正规算子,则有
1)
时,
。
2)
时,
。
显然上述讨论结果对于这样函数的线性组合仍然成立。我们希望得出加权Bergman空间上Toeplitz算子的乘积有限和为亚正规算子的更普遍的结论,但是由于其广泛性和复杂性,目前只能得到上述结论。