交换折叠交叉立方体的Hamilton分解及其性质

The Hamiltonian Decomposition and Its Properties of Exchanged Folded Crossed Cube

摘要: 交换折叠交叉立方体(EFCQ(s,t))是一种用于并行计算的新型互连网络。在这篇文章中，作者证明了s=t=1;2 时，EFCQ(s,t)是Hamilton可分解的；s=t=1;2;3时，EFCQ(s,t)可以分解为一个Hamilton圈和s个完美对集。最后对EFCQ(s,t)的一些性质进行了证明。

Abstract: Exchanged folded crossed cube (EFCQ(s,t)) is a new interconnection network for parallel computation. In this article, author proved EFCQ(s,t) is Hamiltonian decomposition, when s=t=1;2. And EFCQ(s,t) can be decomposed into a Hamiltonian cycle and s perfect matching, when s=t=1;2;3. Finally, some properties of EFCQ(s,t) are proved.

1. 引言

互连网络在并行计算机系统中扮演了十分重要的角色，影响着系统的性能。尤其是在硬件开销，可扩展性，通信性能，可靠性等方面起着决定性的作用。为使大规模的并行计算系统拥有性能高的优点，并且极大地降低成本。选择有效的互连网络拓扑，成为研究界非常关注的重点。刚开始提出的均为一些平凡网络，但这些网络很多都存在不足之处。但随着超立方体网络的诞生，因为其可扩展性，正则性，强容错性以及对称性，这些很好的性质，使得超立方体网络成为并行处理和并行计算机系统常用的拓扑之一，并且得到了非常广泛的应用。与此同时超立方体网络的某些方面又存在一定的不足，为了改进这些现有的问题，超立方体的变型又被相继提出。例如折叠交叉立方体 [1]，交换超立方体 [2]，交换交叉立方体 [3]，交叉超立方体 [4]，莫比乌斯立方体 [4] 等。其中，K. Bhavani和Sudarson Jena在2018年提出交换折叠交叉立方体。交换折叠交叉立方体的出现，相对于互连网络中其他拓扑，在成本和直径上有了实质性的改善。2019年，蔡学鹏，杨伟等人提出交换折叠交叉立方体的连通度和超连通度。

在这篇文章中，证明了交换折叠交叉立方体的正则性以及该网络是一个Hamilton图，并且证明了在 $EFCQ\left(s,t\right)$ 中，若有 $s=t=1;2$，则 $EFCQ\left(s,t\right)$ 是Hamilton可分解的和若有 $s=t=1;2;3$，则 $EFCQ\left(s,t\right)$ 可以分解为一个Hamilton圈和s个完美对集的并。并且给出了 $EFCQ\left(3,3\right)$ 的三条性质。

2. 基本概念

定义1 [5] G的Hamilton圈是指包含G的每个顶点的圈。

定义2 [5] 一个图若包含Hamilton圈，则称这个图是Hamilton图。

定义3 [5] 称图G是k正则的，若对所有 $v\in V$，有 $d\left(v\right)=k$。

定义4 [5] 设M是E的一个子集，它的元素是G中的连杆，并且这些连杆中的任意两个在G中均不相邻，则称M为G的对集(或匹配)；M中的一条边的两个端点称为在M下是配对的；若对集M的某条边与顶点v关联，则称M饱和顶点v，并且称v是M饱和的，否则称v是M非饱和的。若G的每个顶点均为M饱和的，则称M为G的完美对集。

定义5 [6] 设G是正则图， $E\left(G\right)$ 是G的边集，我们称G是Hamilton可分解的，如果

要么a) $\mathrm{deg}\left(G\right)=2k$，且 $E\left(G\right)$ 能被划分成k个Hamilton圈；

要么b) $\mathrm{deg}\left(G\right)=2k+1$，且 $E\left(G\right)$ 能被划分成k个Hamilton圈和一个完美对集。

其中 $\mathrm{deg}\left(G\right)$ 表示G的顶点度。

定义6 [7] [8] [9] $s+t+1$ -维交换折叠交叉立方体网络被定义为一个无向图 $EFCQ\left(s,t\right)=\left(V,E\right)$，其中 $s\ge 1,t\ge 1$。

V是图中顶点的集合，且 $V=\left\{a_{s-1}\cdots a_0{b}_{t-1}\cdots b_{0}c|a_i,b_j,c\in \left\{0,1\right\},i\in \left[0,s-1\right],j\in \left[0,t-1\right]\right\}$。

E是图中边的集合，且E是由四种互不相交的边集 $E_1\cup E_2\cup E_3\cup E_4$ 组成，对任意两个顶点有 $u,v\in V,E_1,E_2,E_3,E_4$，定义如下

1) $\left(u,v\right)\in E_1$，当且仅当 $u\left[0\right]\ne v\left[0\right],u\oplus v=1$ 其中 $\oplus$ 是异或操作。

2) $\left(u,v\right)\in E_2$，当且仅当 $u\left[t:1\right]=v\left[t:1\right],u\left[0\right]=v\left[0\right]=0$ 并且 $\left(u\left[s+t:t+1\right],v\left[s+t:t+1\right]\right)\in E\left(C{Q}_S\right)$。

3) $\left(u,v\right)\in E_3$，当且仅当 $u\left[s+t:t+1\right]=v\left[s+t:t+1\right],u\left[0\right]=v\left[0\right]=1$ 并且 $\left(u\left[t:1\right],v\left[t:1\right]\right)\in E\left(C{Q}_t\right)$。

4) $\left(u,v\right)\in E_4$，当且仅当 $u=\left\{a_{s-1}\cdots a_0{b}_{t-1}\cdots b_{0}c\right\},v=\left\{\overline{a_{s-1}}\cdots \overline{a_0}\overline{b_{t-1}}\cdots \overline{b_0}\bar{c}\right\}$ 且 $\overline{a_i}=1-a_i,\overline{b_j}=1-b_j,\bar{c}=1-c$

$a_i,b_j,c\in \left\{0,1\right\},i\in \left[0,s-1\right],j\in \left[0,t-1\right]$。

3. 主要结果

引理 [7] 在 $EFCQ\left(s,t\right)$ 中二进制字符串最低位为0的点的度为 $s+2$ ；二进制字符串最低位为1的点的度为 $t+2$。

定理1： $EFCQ\left(s,t\right)$ 是正则的，若 $s=t,s\ge 1,t\ge 1$。

$EFCQ\left(s,t\right)$ 是非正则的，若 $s\ne t,s\ge 1,t\ge 1$。

证明：K. Bhavani在文献 [7] 中证明了 $EFCQ\left(s,t\right)$ 的度。在 $EFCQ\left(s,t\right)$ 中二进制字符串最低位为0的点的度为 $s+2$ ；二进制字符串最低位为1的点的度为 $t+2$。故当 $s=t$ 时，在 $EFCQ\left(s,t\right)$ 中，对任意 $v\in V$，都有 $\mathrm{deg}\left(v\right)=s+2$。根据定义3， $EFCQ\left(s,t\right)$ 是正则的。同理，当 $s\ne t$ 时， $EFCQ\left(s,t\right)$ 是非正则的。

定理2： $EFCQ\left(s,t\right)$ 是Hamilton图。

证明：周东仿在文献 [9] 中，提出了Hamiltonian cycle算法，通过调用这个算法可以得到 $ECQ\left(s,t\right)$ 上的一个Hamilton圈。由于 $EFCQ\left(s,t\right)$ 是在 $ECQ\left(s,t\right)$ 的基础上在互补的两个点上增加一条补边所得，根据定义2， $EFCQ\left(s,t\right)$ 是Hamilton图。

定理3：1) $EFCQ\left(1,1\right)$ 是Hamilton可分解的。

2) $EFCQ\left(2,2\right)$ 是Hamilton可分解的。

证明1)：在 $EFCQ\left(1,1\right)$ 中， $\mathrm{deg}\left(EFCQ\left(1,1\right)\right)=3$， $EFCQ\left(1,1\right)$ 是正则图。则根据定义5可知 $EFCQ\left(1,1\right)$ 能被划分成1个边不交的Hamilton圈和1个完美对集的并(如图1)。

Figure 1. $EFCQ\left(1,1\right)$

图1. $EFCQ\left(1,1\right)$ 的图表示

$EFCQ\left(1,1\right)$ 中的Hamilton圈为：

100-101-111-110-010-011-001-000-100

$EFCQ\left(1,1\right)$ 中的完美对集为：

100-011, 101-010, 111-000, 110-001

证明2)：在 $EFCQ\left(2,2\right)$ 中， $\mathrm{deg}\left(EFCQ\left(2,2\right)\right)=4$， $EFCQ\left(2,2\right)$ 是正则图。则根据定义5可知 $EFCQ\left(2,2\right)$ 能被划分成2个边不交的Hamilton圈(如图2)。

$EFCQ\left(2,2\right)$ 中的Hamilton圈 $H_1$ 为：

01000-01001-01011-01010-11010-11011-11001-11000-10000-10001-10011-10010-00010-00011-00111-00110-01110-01111-01101-01100-11100-11101-11111-11110-10110-10111-10101-10100-00100-00101-00001-00000-01000

$EFCQ\left(2,2\right)$ 中的Hamilton圈 $H_2$ 为：

01000-11000-00111-00101-11010-10010-01101-01001-10110-00110-11001-11101-00010-01010-10101-10001-01110-11110-00001-00011-11100-10100-01011-01111-10000-00000-11111-11011-00100-01100-10011-10111-01000

Figure 2. $EFCQ\left(2,2\right)$

图2. $EFCQ\left(2,2\right)$ 的图表示

定理4 1) $EFCQ\left(3,3\right)$ 可以分解为24个8圈16个4圈和一个完美对集并。

2) $EFCQ\left(3,3\right)$ 可以分解为32个4圈16个8圈和一个完美对集并。

3) $EFCQ\left(3,3\right)$ 可以分解为一个Hamilton圈22个4圈5个8圈和一个完美对集的并(如图3)。

图3是 $ECQ\left(3,3\right)$， $EFCQ\left(3,3\right)$ 是在它的基础上增加补边，连接 $ECQ\left(3,3\right)$ 中互补的两个点所得。

证明1)：令 $a_2\in \left\{0,1\right\}$， $EFCQ\left(3,3\right)$ 中有24个8圈其中16个可以表示为：

a₂001011-a₂001010-a₂011010-a₂011011-a₂011111-a₂011110-a₂001110-a₂001111-a₂001011；

a₂001001-a₂001000-a₂011000-a₂011001-a₂011101-a₂011100-a₂001100-a₂001101-a₂001001；

a₂000011-a₂000010-a₂010010-a₂010011-a₂010111-a₂010110-a₂000110-a₂000111-a₂000011；

a₂000001-a₂000000-a₂010000-a₂010001-a₂010101-a₂010100-a₂000100-a₂000101-a₂000001；

a₂101011-a₂101010-a₂111010-a₂111011-a₂111111-a₂111110-a₂101110-a₂101111-a₂101011；

a₂101001-a₂101000-a₂111000-a₂111001-a₂111101-a₂111100-a₂101100-a₂101101-a₂101001；

a₂100011-a₂100010-a₂110010-a₂110011-a₂110111-a₂110110-a₂100110-a₂100111-a₂100011；

a₂100001-a₂100000-a₂110000-a₂110001-a₂110101-a₂110100-a₂100100-a₂100101-a₂100001；

令 $a_2{a}_1{a}_0\in \left\{000,001,010,011,100,101,110,111\right\}$，24个8圈中剩余8个8圈可以表示为：

$a_2{a}_1{a}_{0}1101\text{-}{a}_2{a}_1{a}_{0}1111\text{-}{a}_2{a}_1{a}_{0}0011\text{-}{a}_2{a}_1{a}_{0}0001\text{-}{a}_2{a}_1{a}_{0}1001\text{-}{a}_2{a}_1{a}_{0}1011$ $\text{-}{a}_2{a}_1{a}_{0}0111\text{-}{a}_2{a}_1{a}_{0}0101\text{-}{a}_2{a}_1{a}_{0}1101$

Figure 3. $ECQ\left(3,3\right)$

图3. $ECQ\left(3,3\right)$ 的图表示

令 $b_2{b}_1{b}_{0}c\in \left\{1000,1100,0000,0100\right\},{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\in \left\{1010,1110,0010,0110\right\}$

$EFCQ\left(3,3\right)$ 中有16个4圈可以表示为：

$\begin{array}{l}000b_2{b}_1{b}_{0}c\text{-}010b_2{b}_1{b}_{0}c\text{-}110b_2{b}_1{b}_{0}c\text{-}100b_2{b}_1{b}_{0}c\text{-}000b_2{b}_1{b}_{0}c\\ 001b_2{b}_1{b}_{0}c\text{-}011b_2{b}_1{b}_{0}c\text{-}101b_2{b}_1{b}_{0}c\text{-}111b_2{b}_1{b}_{0}c\text{-}001b_2{b}_1{b}_{0}c\\ 000{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\text{-}010{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\text{-}110{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\text{-}100{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\text{-}000{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\\ 001{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\text{-}011{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\text{-}101{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\text{-}111{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\text{-}001{b^{\prime }}_2{b^{\prime }}_1{b^{\prime }}_0{c}^{\prime }\end{array}$

$EFCQ\left(3,3\right)$ 中的完美对集为M：

0001000-1110111, 0001001-1110110, 0001011-1110100, 0001010-1110101, 0001100-1110011,

0001101-1110010, 0001111-1110000, 0001110-1110001, 0000000-1111111, 0000001-1111110,

0000011-1111100, 0000010-1111101, 0000100-1111011, 0000101-1111010, 0000111-1111000,

0000110-1111001, 0011000-1100111, 0011001-1100110, 0011011-1100100, 0011010-1100101,

0011100-1100011, 0011101-1100010, 0011111-1100000, 0011110-1100001, 0010000-1101111,

0010001-1101110, 0010011-1101100, 0010010-1101101, 0010100-1101011, 0010101-1101010,

0010111-1101000, 0010110-1101001, 0101000-1010111, 0101001-1010110, 0101011-1010100,

0101010-1010101, 0101100-1010011, 0101101-1010010, 0101111-1010000, 0101110-1010001,

0100000-1011111, 0100001-1011110, 0100011-1011100, 0100010-1011101, 0100100-1011011,

0100101-1011010, 0100111-1011000, 0100110-1011001, 0111000-1000111, 0111001-1000110,

0111011-1000100, 0111010-1000101, 0111100-1000011, 0111101-1000010, 0111111-1000000,

0111110-1000001, 0110000-1001111, 0110001-1001110, 0110011-1001100, 0110010-1001101,

0110100-1001011, 0110101-1001010, 0110111-1001000, 0110110-1001001.

即： $EFCQ\left(3,3\right)$ 可以分解为24个8圈16个4圈和一个完美对集M的并。

证明2)：令 $a_2{a}_1{a}_0\in \left\{000,010,100,110\right\},{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_0\in \left\{001,011,101,111\right\}$。

当 $a_2{a}_1{a}_0=000$ 时，同一个圈内 ${a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_0=001$ ； $a_2{a}_1{a}_0=010$ 时，同一个圈内 ${a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_0=011$ ；当 $a_2{a}_1{a}_0=100$ 时，同一个圈内 ${a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_0=101$ ； $a_2{a}_1{a}_0=110$ 时，同一个圈内 ${a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_0=111$。 $EFCQ\left(3,3\right)$ 中的16个8圈可以表示为：

$a_2{a}_1{a}_{0}1000\text{-}{a}_2{a}_1{a}_{0}1001\text{-}{a}_2{a}_1{a}_{0}1011\text{-}{a}_2{a}_1{a}_{0}1010\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}1010\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}1011$ $\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}1001\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}1000\text{-}{a}_2{a}_1{a}_{0}1000$ ；

$a_2{a}_1{a}_{0}1100\text{-}{a}_2{a}_1{a}_{0}1101\text{-}{a}_2{a}_1{a}_{0}1111\text{-}{a}_2{a}_1{a}_{0}1110\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}1110\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}1111$ $\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}1101\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}1100\text{-}{a}_2{a}_1{a}_{0}1100$ ；

$a_2{a}_1{a}_{0}0000\text{-}{a}_2{a}_1{a}_{0}0001\text{-}{a}_2{a}_1{a}_{0}0011\text{-}{a}_2{a}_1{a}_{0}0010\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}0010\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}0011$ $\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_0\text{0001-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}0000\text{-}{a}_2{a}_1{a}_{0}0000$ ；

$a_2{a}_1{a}_{0}0100\text{-}{a}_2{a}_1{a}_{0}0101\text{-}{a}_2{a}_1{a}_{0}0111\text{-}{a}_2{a}_1{a}_{0}0110\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}0110\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}0111$ $\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}0101\text{-}{a^{\prime }}_2{a^{\prime }}_1{a^{\prime }}_{0}0100\text{-}{a}_2{a}_1{a}_{0}0100$ ；

令 $a_2{a}_1{a}_0\in \left\{000,001,010,011,100,101,110,111\right\}$， $EFCQ\left(3,3\right)$ 中的32个4圈其中16个可以表示为：

$a_2{a}_1{a}_{0}1001\text{-}{a}_2{a}_1{a}_{0}1101\text{-}{a}_2{a}_1{a}_{0}0101\text{-}{a}_2{a}_1{a}_{0}0001\text{-}{a}_2{a}_1{a}_{0}1001$ ；

$a_2{a}_1{a}_{0}1011\text{-}{a}_2{a}_1{a}_{0}0111\text{-}{a}_2{a}_1{a}_{0}0011\text{-}{a}_2{a}_1{a}_{0}1111\text{-}{a}_2{a}_1{a}_{0}1011$。

$EFCQ\left(3,3\right)$ 中有32个4圈剩余的16个和定理4 1)的证明中所找到的16个4圈相同。

完美对集为 $EFCQ\left(3,3\right)$ 中的对集M。

即： $EFCQ\left(3,3\right)$ 可以分解为16个8圈32个4圈和一个完美对集M的并。

证明3)： $EFCQ\left(3,3\right)$ 是一个Hamilton图，则可以找到 $EFCQ\left(3,3\right)$ 中有一个Hamilton圈H

0011010-0011011-0010111-0010110-0000110-0000111-0000101-0000100-0010100-0010101-0010001-0010000-0000000-0000001-0000011-0000010-0010010-0010011-0011111-0011110-0001110-0001111-0001101-0001100-0011100-0011101-0011001-0011000-0001000-0001001-0001011-0001010-0101010-0101011-0101001-0101000-0111000-0111001-0111101-0111100-0101100-0101101-0101111-0101110-0111110-0111111-0110011-0110010-0100010-0100011-0100001-0100000-0110000-0110001-0110101-0110100-0100100-0100101-0100111-0100110-0110110-0110111-0111011-0111010-1011010-1011011-1010111-1010110-1000110-1000111-1000101-1000100-1010100-1010101-1010001-1010000-1000000-1000001-1000011-1000010-1010010-1010011-1011111-1011110-1001110-1001111-1001101-1001100-1011100-1011101-1011001-1011000-1001000-1001001-1001011-1001010-1101010-1101011-1101001-1101000-1111000-1111001-1111101-1111100-1101100-1101101-1101111-1101110-1111110-1111111-1110011-1110010-1100010-1100011-1100001-1100000-1110000-1110001-1110101-1110100-1100100-1100101-1100111-1100110-1110110-1110111-1111011-1111010-0011010

除去H所占用的边， $EFCQ\left(3,3\right)$ 中剩余的边可以分解为的5个8圈22个4圈和一个完美对集的并。

其中所分解的5个8圈为：

0011001-0011011-0011111-0011101-0010101-0010111-0010011-0010001-0011001；

0111001-0111011-0111111-0111101-0110101-0110111-0110011-0110001-0111001；

1011001-1011011-1011111-1011101-1010101-1010111-1010011-1010001-1011001；

1111001-1111011-1111111-1111101-1110101-1110111-1110011-1110001-1111001；

0001010-0011010-0111010-0101010-1101010-1111010-1011010-1001010-0001010。

$EFCQ\left(3,3\right)$ 中的22个4圈，其中14个4圈为定理4 1)证明中所找到的16个4圈中除去两个4圈0001010-0101010-1101010-1001010-0001010；0011010-0111010-1011010-1111010-0011010所得。

令 $a_2{a}_1{a}_0\in \left\{000,010,100,110\right\}$，22个4圈中剩余的8个4圈则可以表示为：

$a_2{a}_1{a}_{0}1001\text{-}{a}_2{a}_1{a}_{0}1101\text{-}{a}_2{a}_1{a}_{0}0101\text{-}{a}_2{a}_1{a}_{0}0001\text{-}{a}_2{a}_1{a}_{0}1001$ ；

$a_2{a}_1{a}_{0}1011\text{-}{a}_2{a}_1{a}_{0}0111\text{-}{a}_2{a}_1{a}_{0}0011\text{-}{a}_2{a}_1{a}_{0}1111\text{-}{a}_2{a}_1{a}_{0}1011$。

完美对集为 $EFCQ\left(3,3\right)$ 中的对集M。

即： $EFCQ\left(3,3\right)$ 可以分解为一个Hamilton圈5个8圈22个4圈和一个完美对集M的并。

定理5 1) $EFCQ\left(1,1\right)$ 可以分解为一个Hamilton圈和1个完美对集的并。

2) $EFCQ\left(2,2\right)$ 可以分解为一个Hamilton圈和2个完美对集的并。

3) $EFCQ\left(3,3\right)$ 可以分解为一个Hamilton圈和3个完美对集的并。

证明1)：根据定理3 1)的证明，显然可得。

证明2)：根据定理3 2)的证明， $EFCQ\left(2,2\right)$ 中有一个Hamilton圈为 $H_1$。

它的完美对集为 $M_1,M_2$

M₁: 01000-11000, 01100-00100, 00000-10000, 11100-10100, 01010-00010, 01110-11110, 00110-10110, 11010-10010, 01001-01101, 01011-01111, 00001-00011, 00101-00111, 11001-11101, 11011-11111, 10001-10101, 10011-10111.

M₂: 01000-10111, 01001-10110, 01011-10100, 01010-10101, 01100-10011, 01101-10010, 01111-10000, 01110-10001, 00000-11111, 00001-11110, 00011-11100, 00010-11101, 00100-11011, 00101-11010, 00111-11000, 00110-11001.

证明3)：根据定理2， $EFCQ\left(3,3\right)$ 是一个Hamilton图。已知 $EFCQ\left(3,3\right)$ 中有一个Hamilton圈H。除去H所包含的边，将剩余的边割裂为九块 $E_a,E_b,E_c,E_d,E_e,E_f,E_g,E_h,E_i$，

E_a: 0001000-0101000, 0001100-0101100, 0000000-0100000, 0000100-0100100, 0011000-0111000, 0011100-0111100, 0010000-0110000, 0010100-0110100, 1001000-1101000, 1001100-1101100, 1000000-1100000, 1000100-1100100, 1011000-1111000, 1011100-1111100, 1010000-1110000, 1010100-1110100.

E_b: 0001010-0011010, 0001110-0101110, 0000010-0100010, 0000110-0100110, 0011110-0111110, 0010010-0110010, 0010110-0110110, 0101010-0111010, 1001010-1011010, 1001110-1101110, 1000010-1100010, 1000110-1100110, 1011110-1111110, 1010010-1110010, 1010110-1110110, 1101010-1111010.

E_c: 0001000-1001000, 0001100-1001100, 0000000-1000000, 0000100-1000100, 0011000-1111000, 0011100-1111100, 0010000-1110000, 0010100-1110100, 0101000-1101000, 0101100-1101100, 0100000-1100000, 0100100-1100100, 0111000-1011000, 0111100-1011100, 0110000-1010000, 0110100-1010100.

E_d: 0001010-1001010, 0001110-1001110, 0000010-1000010, 0000110-1000110, 0011010-0111010, 0011110-1111110, 0010010-1110010, 0010110-1110110, 0101010-1101010, 0101110-1101110, 0100010-1100010, 0100110-1100110, 0111110-1011110, 0110010-1010010, 0110110-1010110, 1011010-1111010.

E_e: 0001001-0001101, 0000001-0000101, 0011101-0010101, 0011001-0010001, 0011011-0011111, 0010011-0010111, 0101001-0101101, 0100001-0100101, 0111101-0110101, 0111001-0110001, 0111011-0111111, 0110011-0110111, 1001001-1001101, 1000001-1000101, 1011101-1010101, 1011001-1010001, 1011011-1011111, 1010011-1010111, 1101001-1101101, 1100001-1100101, 1111101-1110101, 1111001-1110001, 1111011-1111111, 1110011-1110111.

E_f: 0001101-0000101, 0001001-0000001, 0011001-0011011, 0011101-0011111, 0010001-0010011, 0010101-0010111, 0101101-0100101, 0101001-0100001, 0111001-0111011, 0111101-0111111, 0110001-0110011, 0110101-0110111, 1001101-1000101, 1001001-1000001, 1011001-1011011, 1011101-1011111, 1010001-1010011, 1010101-1010111, 1101101-1100101, 1101001-1100001, 1111001-1111011, 1111101-1111111, 1110001-1110011, 1110101-1110111.

E_g: 0001011-0001111, 0000011-0000111, 0100011-0100111, 0101011-0101111, 1001011-1001111, 1000011-1000111, 1101011-1101111, 1100011-1100111.

E_h: 0001111-0000011, 0001011-0000111, 0101111-0100011, 0101011-0100111, 1001111-1000011, 1001011-1000111, 1101111-1100011, 1101011-1100111.

$E_i=E(\; M\; )$

我们所割裂的九块，可以组成17种完美对集分别为：

$\begin{array}{l}{M}_1,M_2,M_3,M_4,M_5,M_6,M_7,M_8,M_9,M_{10},M_{11},M_{12},M_{13},M_{14},M_{15},M_{16},M\\ M_1=\left(E_a\cup E_b\cup E_e\cup E_g\right),M_2=\left(E_a\cup E_b\cup E_f\cup E_h\right),M_3=\left(E_a\cup E_b\cup E_e\cup E_h\right),\\ M_4=\left(E_a\cup E_b\cup E_f\cup E_g\right),M_5=\left(E_c\cup E_d\cup E_f\cup E_h\right),M_6=\left(E_c\cup E_d\cup E_e\cup E_g\right)\\ M_7=\left(E_c\cup E_d\cup E_e\cup E_h\right),M_8=\left(E_c\cup E_d\cup E_f\cup E_g\right),M_9=\left(E_c\cup E_b\cup E_e\cup E_g\right)\end{array}$

$\begin{array}{l}{M}_{10}=\left(E_c\cup E_b\cup E_f\cup E_h\right),M_{11}=\left(E_c\cup E_b\cup E_e\cup E_h\right),M_{12}=\left(E_c\cup E_b\cup E_f\cup E_g\right)\\ M_{13}=\left(E_a\cup E_d\cup E_f\cup E_h\right),M_{14}=\left(E_a\cup E_d\cup E_e\cup E_g\right),M_{15}=\left(E_a\cup E_d\cup E_e\cup E_h\right)\\ M_{16}=\left(E_a\cup E_d\cup E_f\cup E_g\right)\end{array}$

$\begin{array}{l}E\left(EFCQ\left(3,3\right)\right)\\ =E\left(H\right)\cup E\left(M\right)\cup E\left(M_1\right)\cup E\left(M_5\right)=E\left(H\right)\cup E\left(M\right)\cup E\left(M_2\right)\cup E\left(M_6\right)\\ =E\left(H\right)\cup E\left(M\right)\cup E\left(M_3\right)\cup E\left(M_8\right)=E\left(H\right)\cup E\left(M\right)\cup E\left(M_4\right)\cup E\left(M_7\right)\\ =E\left(H\right)\cup E\left(M\right)\cup E\left(M_9\right)\cup E\left(M_{13}\right)=E\left(H\right)\cup E\left(M\right)\cup E\left(M_{10}\right)\cup E\left(M_{14}\right)\\ =E\left(H\right)\cup E\left(M\right)\cup E\left(M_{11}\right)\cup E\left(M_{16}\right)=E\left(H\right)\cup E\left(M\right)\cup E\left(M_{12}\right)\cup E(\; M\; 15\; )\end{array}$

即： $EFCQ\left(3,3\right)$ 可以分解为一个Hamilton圈和三个完美对集的并。

4. 结束语

交换折叠交叉立方体网络作为一种新型的互连网络，具有非常重要的意义。本文中给出了 $EFCQ\left(s,t\right)$ 相关定理，对低维的交换折叠交叉立方体的Hamilton可分解性做了证明，但对于 $s=t\ge 3$ 的情况， $EFCQ\left(s,t\right)$ 是否是Hamilton可分解的以及 $s=t\ge 4$ 情况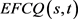，是否可以分解为一个Hamilton圈和s个完美对集的问题仍需要进一步研究证明。