1. 引言
Lotka-Volterra系统
描述的是群落中
个种群相互之间的作
用关系,其中
表示第i个种群的密度,
表示第i个种群的内禀增长率,
代表第j个种群对第i个种群的影响 [1],
和
的正负性代表第i个种群和第j个种群的相互关系。本文主要讨论Lotka-Volterra多种群互惠系统。
Goh [2] 给出了两个种群情况下的互惠系统:
,
。若
且
,那么
是系统的唯一正平衡点,
下面我们在系统中引入白噪声。设
,
是初值为0的G-布朗运动,
是白噪声的强度。从而有:
2. 次线性期望和G-布朗运动
本章我们简要回顾了一些G-布朗运动的基本结果 [3] [4]。设
是给定的集合,向量格
是定义在
上的实值函数所组成的一个线性空间,同时有:每一个实值的常数c都在
中;如果
,则也有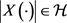 。
。
定义2.1. 一个次线性期望
是定义在随机变量空间
上的满足以下性质的泛函:对于所有的随机变量
,有
1) 单调性:若
;
2) 保常数性:
;
3) 次线性:
;
4) 正齐次性:
。
称三元组
为次线性期望空间。
令
表示所有满足
的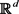 -实值连续轨道
所成的空间,定义其上的距离为:
-实值连续轨道
所成的空间,定义其上的距离为:
表示Ω上的Borel
-代数,令
上的典则过程,对每一确定的
,令
且
其中
是
上所有有界的Lipschitz函数的集合,因此,在
上,我们可以定义典则次线性期望
使得典则过程
是G-布朗运动。这个次线性期望通常称为G-期望,记作
。对每个
,我们令
表示
在范数
下的完备。
定义2.2. (G-正态分布) 次线性期望空间
上的d维随机向量
称作G-正态分布,如果对每个
,有
,
其中
是X的一个独立版本。
G- 正态分布的随机向量X满足下面的特性 [4]:
引理2.1. 令X为d维G-正态分布的随机向量,那么可以由
刻画X的分布。
是G-热方程
定义在
上的唯一黏性解,其中
是
的Hessian矩阵,定义
为:
是
对称矩阵空间。
,其中,
。
定义2.3. (G-布朗运动) 次线性期望空间
上的d维过程
称为G-布朗运动,如果满足以下性质:
1)
;
2) 对每个
,增量
独立于
,
且
;
3) 对每个
,
,其中X是G-正态分布的。
对
,我们介绍下列空间:
:所有
-可测实函数所成空间,
:所有
-可测实函数所成空间。对给定的
的分划
,令
其中,
,我们将这类过程的集合记作
。
对
,定义其Bochner积分和Itô积分如下:
及
对
,
表示
在范数
下的完备。
引理2.2. 映射
是一个线性的连续映射.因此,可以连续地延拓至
。有:
引理2.3. 对
,令
,
,固定
,
是
上的n维过程,且具有以下形式:
其中,对
,
,
和
在
中有界,
是
中给定的随机向量,在
中,我们有:
通过Denis等人的方法 [5],我们可以将G-期望的域从
扩展到
。
用
表示:
其中,
是
上鞅测度的弱紧集。
3. 系统的存在性
3.1. 系统正解的存在性
对于Lotka-Volterra多种群互惠系统(1):
设
条件1 矩阵
是不可约的,且
,
。
定理3.1. 若条件1成立,则对任意初值
,系统(1)存在唯一的正解
,且该解以概率1位于
中,即对所有的
q.s.。
证明 由于系统(1)的系数满足局部Lipschitz条件,那么对
,存在唯一的局部解
,其中
表示爆破时刻(可参见Arnold [6]、Freedman [7]、Mao [8] )。证明该解是全局存
在的,只需证明
q.s.设
满足
。对每一个整数
,定义停时:
此处及后面总假设
。显然,随着
,
是递增的。令
,则
q.s.因此要证
q.s.,只需证明
q.s.,并且此时显然满足
q.s.。换而言之,完成该定理的证明只需证明
q.s.。如若不然,存在常数
和
使得
。从而存在整数
满足
,对所有的
。
定义
函数
:
,其中
表示
的第i个对角元的余子式(见引理A.1.)。由附录A中引理A.1.的结论可知
,则函数
是正定的。由Itô公式可得
其中
由于矩阵A不可约,由附录A中引理A.3。
从而
可得
这里K是正常数。
从而
取G-期望可得
其中
对
,令
,可得
。注意到对每个
,
或者
。
于是,
不小于
或者
。
即
其中
表示集合
的示性函数。令
,得
矛盾。因此必有
q.s.定理得证。
3.2. 系统(1)存在平稳分布且具有遍历性
设非其次线性方程
(2)
其中
如前所定义,
。定义矩阵
其中
是正常数。
引理3.1. 若
且条件1成立,有
引理3.2. 若条件1 满足,那么方程(2)存在正解。
是
中一自治Markov过程,那么它可表示以下随机微分方程的解:
方程的扩散阵:
假设B:存在具有正则边界
的有界区域
满足:
(B.1.) 在U和它的一些邻域,扩散阵
的最小特征值是非零的。
(B.2.) 当
时,从x出发的轨道到达集合U的平均时间
是有限的,且对每个紧子集
有
。
引理3.3. 如果上述假设成立,那么Markov过程
存在平稳分布
。令
为关于测度
可积的函数。则对所有的
成立
引理3.4. 设
为
中的正则Markov过程。若
相对于某个有界区域U是常返的,则它相对于
中的任一非空区域是常返的。
注记3.1. 定理3.1.给出了系统(1)存在唯一的正解
。另外,由定理3.1.的证明得到了
,现定义
,则
,且显然有
, 当
,
其中
。因此由Khas’minskii [9] 给出
是
中的自治Markov过程。
定理3.2. 假设条件1成立,且
满足
其中
如定理3.1.证明中所定义,
是方程(2)的正解,则系统(1)存在平稳分布
且具有遍历性。
证明 定义
由于矩阵
是不可约的,则由引理A.1.可知
。此外由引理3.2.可知方程(2)存在正解
满足
于是
是正定的。由Itô公式并结合上式可得
其中,
由于
则椭圆
全部落于
中。选取U是包含
的一个邻域,使得当
,有
(C为正常数),这表明假设B中的条件(B.2.)满足。因此解
在区域U是常返的,结合引理3.4.和注记3.1.可知
在
中的任意有界区域D是常返的。
另一方面,对任意的
,设
那么对
,有
所以条件(B.1.)也满足。由此系统(1)存在平稳分布
且具有遍历性。
附录A
在本节中,我们介绍上面证明中使用的一些图论知识。
一有向图
包含定点集
和一个有向线
(表示从k到终点j)的集合E。若对有向线
赋予一正的值
,则图
是有权重的。给定一个具有n个顶点的权重图
,其中
表示权重矩阵,若
存在则表示有向线
的权重,否则为0。称有向图
是强相关的,若
任意两个不同顶点之间存在从这一点到另一点的路。一个权重的有向图
是强相关的当且仅当权重矩阵A是不可约的。
的Laplacian矩阵定义如下
设
表示矩阵
的第k个对角元的余子式,则其具有如下性质。
引理A.1. 设
,那么
其中,
是
以顶点k为根的生成树
的集合,并且
是
的权重。特别地,若有向图
是强相关的,则对
,
。
引理A.2. 设
且矩阵A是不可约的,则线性系统
的解空间的维度为1,且
是解空间的基础解,其中,
如引理A.1.中所定义。
引理A.3. 设
且
如引理A.1.中所定义,则如下等式成立
其中
是任意函数。