1. 引言
80年代初在应力筛选迅速发展的同时,人们就已经注意到由于设计潜在缺陷残留量仍不少,为可靠性的提高提供了可观的空间,另外还有价格和研制周期问题,这是当今动态市场竞争的焦点,实践证明可靠性强化试验(RET)正是综合解决这一问题的最好方法 [1],目前可靠性强化试验在许多行业得到了应用 [2] [3] [4] [5] [6]。要实施强化应力必须要有相应的设备,沿用传统的试验设备进行RET也能取得某种程度的成功,但试验时需换向麻烦,价格也贵,无法满足RET的要求。因此,一种崭新的高效廉价的气动可靠性强化试验台应运而生 [7] [8]。
目前国外可靠性强化试验设备研发主要集中在美国,CSZ、Qualmark和Hanse都是做HALT/HASS试验系统的知名公司,已设计出多个系列产品。相对于国外而言,国内对可靠性强化试验技术与设备的研究起步较晚。目前,国防科技大学可靠性实验室在强化试验技术研究及应用方面开展了大量工作,对试验台的振动信号生成机理及性能 [9]、气锤组合方式对台体性能的影响 [10]、振动低频能量的改善 [11] 等方面进行了理论研究,虽然未设计出成熟的产品,但为国内自主设计相应的可靠性强化试验设备奠定了理论基础。北京航空航天大学可靠性工程中心也在可靠性试验分析方面取得了一些成果。国内尚无自主研发的可靠性强化试验台成熟产品,缺乏实际设计经验,因此在设计初期需要借助数值仿真手段来指导设计。
LS-Dyna是世界上最著名的通用显示动力分析程序,尤其适合于仿真高速碰撞、爆炸和金属成型等非线性动力冲击问题 [12]。气动可靠性强化试验台的振源为气锤产生的往复冲击激振力,故采用Ansys的LS-Dyna模块对这一过程进行瞬态动力学数值仿真。
2. 试验台基本工作原理
气动试验台简图如图1所示,试验台主要包括台板、气锤和支撑弹簧和安装支架四个主要部分,台板为空心结构,底部安装有多个激振气锤,通入压缩空气后,气锤内部活塞往复运动撞击前端垫块产生冲击激振力使整个台板发生振动。
试验台最基本的性能参数是台面冲击响应加速度信号的有效值。当气锤设计好之后,其最大激振力是固定的,此时台面冲激响应的加速度有效值可能会受到支承弹簧刚度和支承位置以及大小气锤组合方式的影响,因此需要通过仿真分析来确定最佳的支撑弹簧刚度及安装位置以及气锤的组合方式。
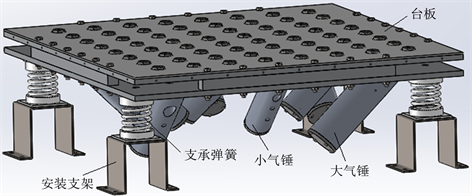
Figure 1. Curve: schematic diagram of reliability enhancement testing rig
图1. 可靠性强化试验台简图
气锤是整个系统的动力源,其内部结构如图2所示。
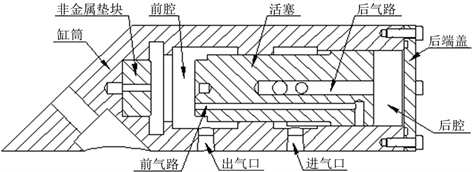
Figure 2. Curve: internal structure of the excitation hammer
图2. 激振气锤内部结构
气锤在往复运动的一个周期内可以划分为四个阶段,活塞初始在重力的作用下与后端盖接触。当进气口通入压缩空气时,进气口与后气路连通,压缩空气进入后腔,活塞加速运动,直到进气口与后气路隔断,不再进气。之后原有压力推动活塞继续前进,做加速度减小的加速运动,直到后腔中的压缩空气经后气路上的通孔与排气口接通,后腔气压迅速降低,同时进气口通过前气路和前腔连通,活塞同时克服重力和前腔气体的阻力而减速运动,直至撞击非金属垫块。撞击后在反弹力、前端面大气压力和重力合力作用下回程,回程运动到一定位置之后,进气口又与后腔接通,后腔压力增大,回程速度减小直至停止,此时运动一个周期结束。随后活塞又在后腔压力作用下重复往复运动,为气动可靠性强化试验台提供周期性的冲击激励。
文献 [13] 对气锤激振信号的产生机理进行了详细的建模分析,本文不再赘述,在后续仿真模型建立过程中直接利用文献得出的激振力时域表达式来进行力的加载。
3. 仿真分析过程
3.1. 分析方案规划
气动可靠性强化试验台主要由台板,支撑弹簧和激振气锤组成,可能影响到试验台的加速度响应的主要方面包括激振力的性质、支撑弹簧的刚度大小和安装位置,以及激振气锤的安装位置和组合方式。
激振力的性质通过建立激振气锤的物理模型和数学模型进行理论分析计算获得。激振气锤的安装位置受到结构的限制,不易改变并且需对称分布,因此仿真采用9个固定的气锤安装位置,气锤与下板的夹角均为45˚。激振气锤在下板上的安装位置如图3所示。
主要从三个方面进行仿真:1) 支撑弹簧刚度的大小对台板中心加速度响应的影响;2) 支撑弹簧的安装位置对台板中心加速度响应的影响;3) 气锤组合方式对台板中心加速度响应的影响。
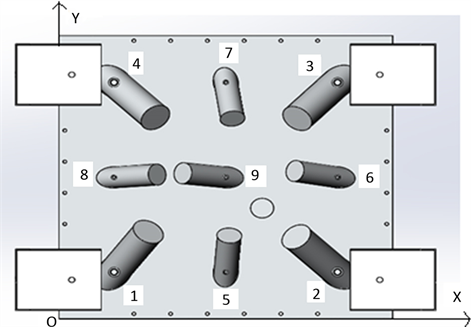
Figure 3. Curve: installation form of the air hammer
图3. 激振气锤的安装形式
3.2. 建模与网格划分
根据初步设计的台面结构尺寸建立空心台板的三维模型,保存成x_t类型的文件,并且文件名不可出现中文,以保证模型能够正确导入Ansys中。
定义SOLID164、COMBI165和MASS166三种类型的单元,设置对应的实常数。SOLID164用于对空心台板的网格划分,COMBI165用来模拟弹簧,MASS166模拟9个气锤的质量。
建立各向同性弹性模型和线弹性弹簧模型两种材料模型,其中线弹性弹簧模型是采用COMBI165单元必不可少的。
为保证划分网格的质量,用工作平面对空心台板进行切割后再进行网格划分(注意切割后一定要进行Glue),通过线尺寸控制来控制网格大小,最终有限元模型如图4所示。
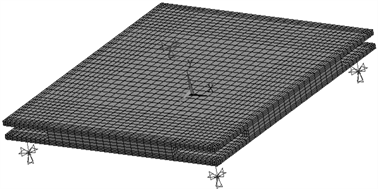
Figure 4. Curve: finite element model of the table
图4. 试验台有限元模型
3.3. 约束与气锤激振力的施加
为4个COMBI165弹簧单元不与空心台板相连的节点添加约束,每个节点约束三个自由度的位移和三个自由度的转动。
由于气锤结构复杂,直接将气锤加入整个仿真模型很难实现,因此将9个气锤锤击力直接以力的形式加载,需要确定冲击力的表达式。根据理论分析得出气锤冲击产生冲击力的解析式为 [13]:
(1)
其中:
;
为撞击瞬间活塞速度;
为气缸横截面积;
为气缸弹性模量;
为非金属
垫块横截面积;
为非金属垫块弹性模量;
为气缸中压缩波波速;
为活塞质量;
为非金属垫块泊松比;
为非金属垫块厚度。
可以根据初步设计的大小气锤的结构和尺寸参数由公式(1)计算出大小气锤的单周期冲击力,再根据大小气锤冲击信号的周期进行延拓即可得到实际的多周期激振力信号。
得到大小气锤多周期激振力信号曲线后通过命令流进行曲线形式的力加载,注意加载力的方向需要在节点坐标系中确定。
3.4. 结果处理
选择时间历程后处理器POST26进行后处理以获得随时间变化的结果数据,在时间历程变量对话框中添加台板中心位置的节点变量后即可进行结果的图形显示。
4. 结果分析与验证
4.1. 仿真分析结果
4.1.1. 弹簧安装位置对台板中心加速度响应的影响
弹簧刚度均保持10,000 N/m不变,气锤用4大5小的组合方式,仅改变弹簧的支撑位置。4个弹簧在下板上是对称分布的,弹簧支撑位置到相邻两边距离D相等,分别取为55 mm、60 mm、65 mm,对比结果见图5~7。
根据以上仿真结果对比可以看出弹簧安装位置对上板中心位置加速度响应影响非常小,考虑到弹簧安装盘和气锤不能发生干涉,选择弹簧安装位置见表1:
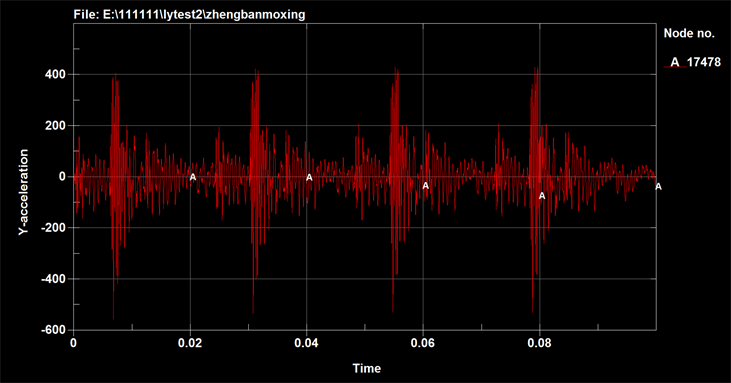
Figure 5. Curve: acceleration response at the table’s center (D = 55 mm)
图5. 台板中心加速度响应(D = 55 mm)
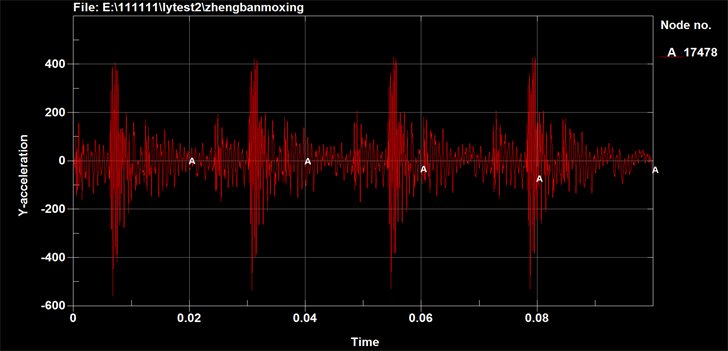
Figure6. Curve: acceleration response at the table’s center (D = 60 mm)
图6. 台板中心加速度响应(D = 60 mm)
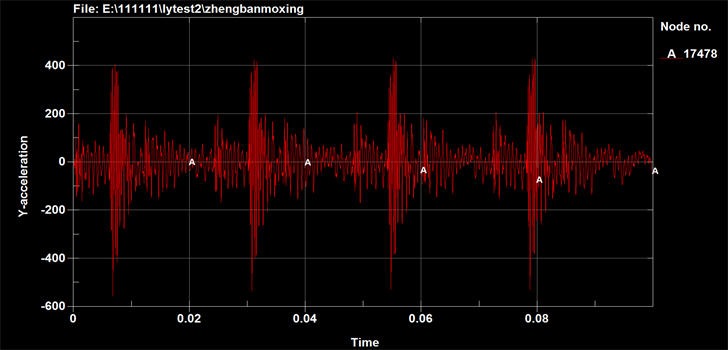
Figure7. Curve: acceleration response at the table’s center (D = 65 mm)
图7. 台板中心加速度响应(D = 65 mm)

Table 1. Coordinates of the springs’ install locations
表1. 弹簧安装位置坐标
4.1.2. 弹簧刚度对台板中心加速度响应的影响
气锤用4大5小的组合方式,按表1位置安装,弹簧支撑位置按表2确定,且保持不变,仅改变弹簧刚度K。弹簧刚度K分别取为10,000 N/m、25,500 N/m、255,000 N/m,台板中心位置加速度响应相应结果见图8~10。
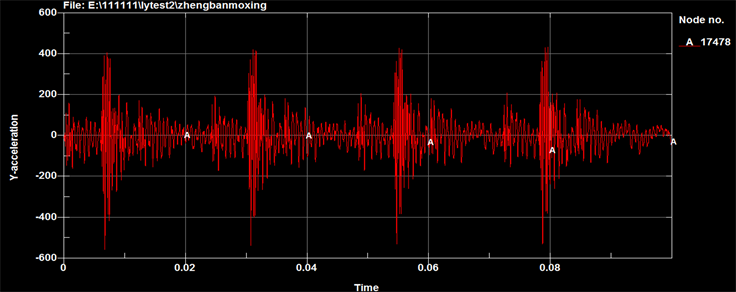
Figure8. Curve: acceleration response at the table’s center (K = 10,000 N/m)
图8. 台板中心加速度响应(K = 10,000 N/m)
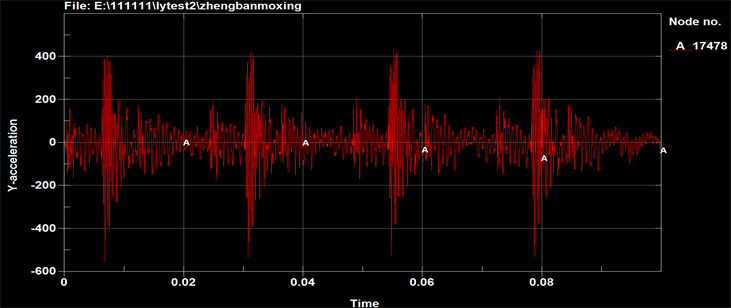
Figure9. Curve: acceleration response at the table’s center (K = 25,500 N/m)
图9. 台板中心加速度响应(K = 25,500 N/m)
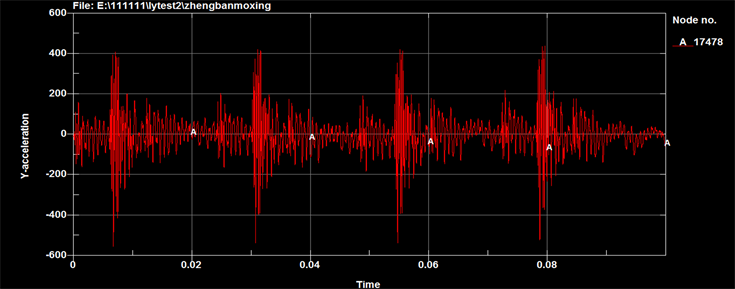
Figure10. Curve: acceleration response at the table’s center (K = 255,000 N/m)
图10. 台板中心加速度响应(K = 255,000 N/m)
对比不同弹簧刚度下的台板中心加速度响应,可以看出加速度基本无差别。在不同刚度下,台板中心位移响应如图11~13所示。
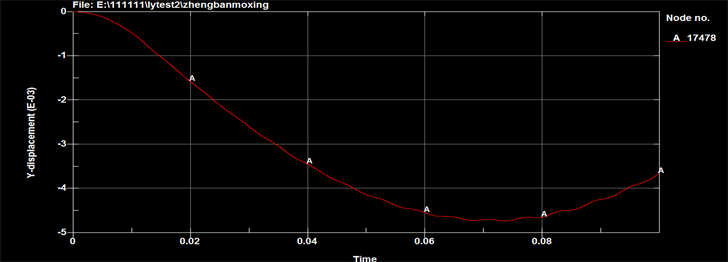
Figure11. Curve: displacement response at the table’s center (K = 10,000 N/m)
图11. 台板中心位移响应(K = 10,000 N/m)
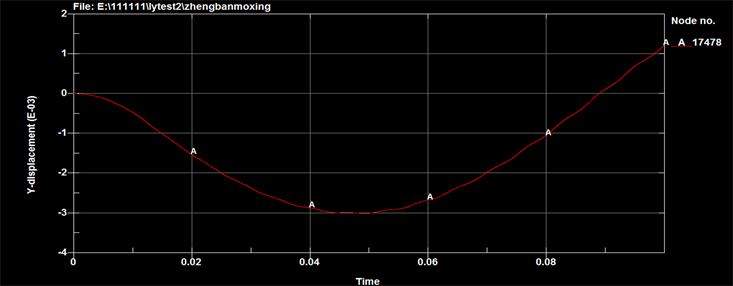
Figure12. Curve: displacement response at the table’s center (K = 25,500 N/m)
图12. 台板中心位移响应(K = 25,500 N/m)
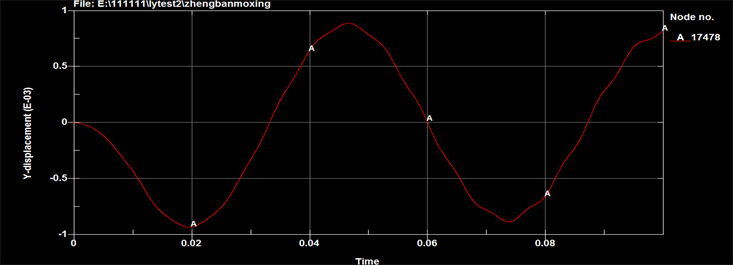
Figure13. Curve: displacement response at the table’s center (K = 255,000 N/m)
图13. 台板中心位移响应(K = 255,000 N/m)
通过对比不同弹簧台板中心位置位移响应可以看出,弹簧刚度变化影响的是低频,会影响到位移的峰值和频率,但对于加速度信号来说受到这个低频的影响非常小,可以忽略。因此设计弹簧刚度时只需满足承载要求即可,最终选择弹簧刚度为25,500 N/m。
4.1.3. 气锤组合方式对台板中心加速度响应的影响
按表1选择弹簧支撑位置,刚度均为25,500 N/m。仅改变气锤的组合方式进行仿真,共分为五种组合方式,组合1为全部小气锤,组合2为全部大气锤,组合3为4大5小(四个角大气锤,其余小气锤),组合4为5大4小(四角小气锤,其余大气锤),组合5为4大5小(四角和中心小气锤,其余大气锤),各组合方式下的仿真结果如图14~18所示。
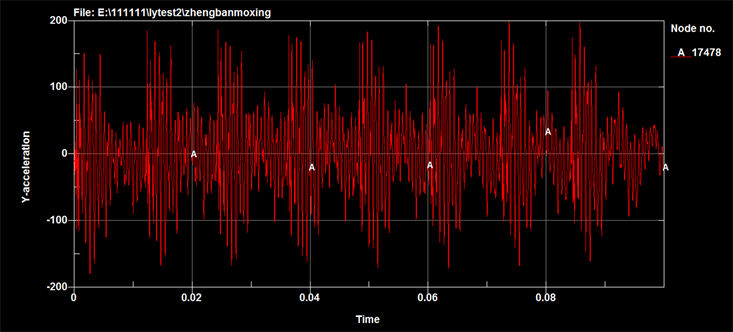
Figure 14. Curve: acceleration response at the table’s center (combination mode 1)
图14. 台板中心加速度响应(组合方式1)
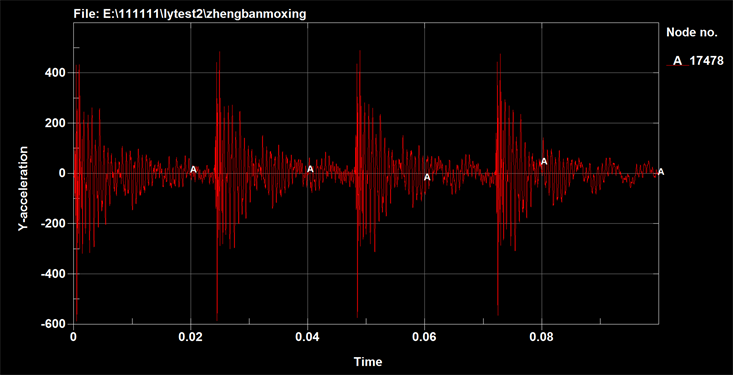
Figure 15. Curve: acceleration response at the table’s center (combination mode 2)
图15. 台板中心加速度响应(组合方式2)
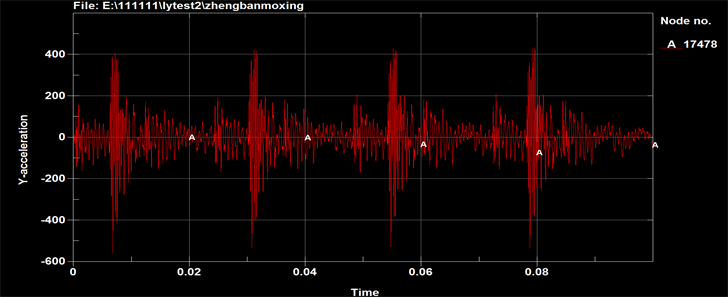
Figure 16. Curve: acceleration response at the table’s center (combination mode 3)
图16. 台板中心加速度响应(组合方式3)
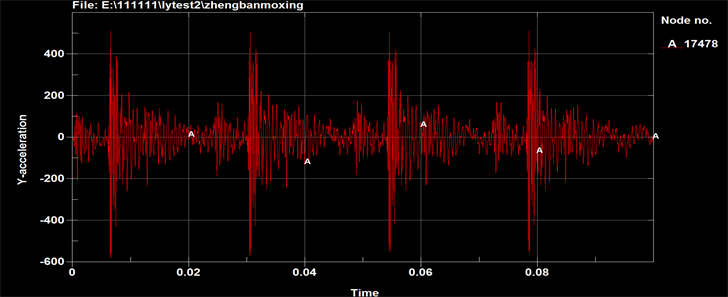
Figure 17. Curve: acceleration response at the table’s center (combination mode 4)
图17. 台板中心加速度响应(组合方式4)
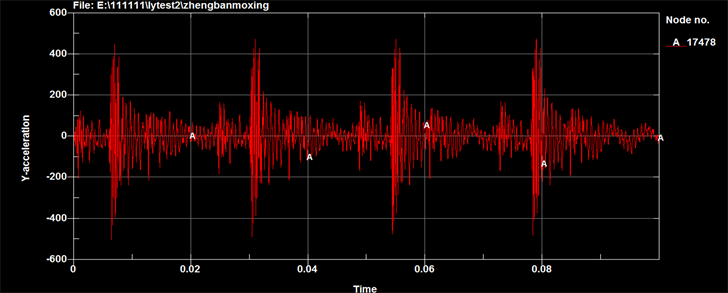
Figure 18. Curve: acceleration response at the table’s center (combination mode 5)
图18. 台板中心加速度响应(组合方式5)
对五种组合方式的上台板中心位置加速度响应计算有效值,结果如表2所示:

Table 2. Grms at the center of the table under different air hammers’ combinations
表2. 不同气锤组合方式下台板中心点加速度有效值
可以看出,虽然大气锤的冲击力幅值比小气锤大,但是大气锤冲击频率比小气锤低,因此大小气锤组合比全部采用大气锤加速度有效值大。根据仿真结果比较,为取得更大的加速度有效值,采用5大4小的组合方式,四角和中心安装大气锤,其余四处安装小气锤。
4.2. 实际测试结果
根据以上仿真结果,最终设计弹簧刚度为25,500 N/m,安装位置见表2。选择5大4小(四角大)的气锤组合方式,按照表1位置安装,轴线与台板侧面平行,与台板低面的夹角45˚。试验台实物如图19所示。
在实际的台板中心位置安装加速度传感器,全部气锤通入0.2 Mpa压缩空气,试验台空载工作,采集实际的加速度响应数据,结果见图20。

Figure 19. Curve: physical diagram of the testing bench
图19. 试验台实物图
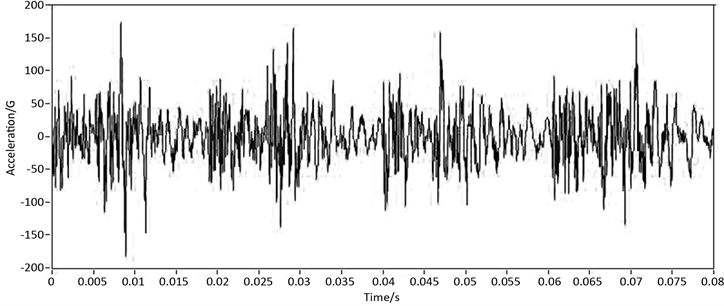
Figure 20. Curve: measured acceleration response at the table’s center
图20. 实测台面中心加速度响应
实测结果的加速度响应曲线与仿真响应曲线形状相近,可以证实仿真方法的有效性。
5. 结论
根据可靠性强化试验台的结构原理,建立试验系统的有限元模型,模型直接应用理论分析的气锤激振力表达式进行力的加载,避免了气锤直接参与仿真带来的流固耦合问题。通过简化的有限元仿真模型的仿真分析确定了试验台合理的结构尺寸参数及气锤布置方案。通过与实际测试结果的比较可以证实Ansys/LS-Dyna仿真模型的合理性,对可靠性强化试验台的研发设计具有一定的指导意义。