欧氏空间中完备自收缩子的刚性定理
A Rigidity Theorem for Complete Self-Shrinkers in the Euclidean Space
DOI: 10.12677/AAM.2020.912246, PDF,    科研立项经费支持
作者: 曹顺娟：浙江农林大学数学系，浙江 杭州
关键词: 完备自收缩子；刚性定理；第二基本形式；Complete Self-Shrinker； Rigidity Theorem； Second Fundamental Form
摘要: 对欧氏空间中的完备自收缩子M，我们证明：如果第二基本形式A满足，且平均曲率向量满足，那么M等距于下列广义柱面之一：，。
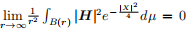
Abstract: For a complete self-shrinker M in the Eulidean space Rn+p, we prove that if the second fundamental form A satisfies and the mean curvature H satifies , then M is one of the generalized cylinders , .
文章引用：曹顺娟. 欧氏空间中完备自收缩子的刚性定理[J]. 应用数学进展, 2020, 9(12): 2123-2128. https://doi.org/10.12677/AAM.2020.912246

参考文献

[1] Abresch, U. and Langer, J. (1986) The Normalized Curve Shortening Flow and Homothetic Solutions. Journal of Differential Geometry, 23, 175-196. [Google Scholar] [CrossRef] 
[2] Huisken, G. (1990) Asymptotic Behavior for Singularities of the Mean Curvature Flow. Journal of Differential Geometry, 31, 285-299. [Google Scholar] [CrossRef] 
[3] Huisken, G. (1993) Local and Global Behavior of Hypersurfaces Moving by Mean Curvature. In: Differential Geometry: Partial Differential Equations on Manifolds (Los Angeles, Calif, 1990), Proceedings of Symposia in Pure Mathematics, Vol. 54, American Mathematical Society, RI, 175-191. [Google Scholar] [CrossRef] 
[4] Colding, T.H. and Minicozzi II, W.P. (2012) Generic Mean Curvature Flow I; Generic Singu- larities. Annals of Mathematics, 175, 755-833. [Google Scholar] [CrossRef] 
[5] Le, N. and Sesum, N. (2011) Blow-Up Rate of the Mean Curvature during the Mean Curvature Flow and a Gap Theorem for Self-Shrinkers. Communications in Analysis and Geometry, 19, 633-659. [Google Scholar] [CrossRef] 
[6] Cao, H.D. and Li, H.Z. (2013) A Gap Theorem for Self-Shrinkers of the Mean Curvature Flow in Arbitrary Codimension. Calculus of Variations and Partial Differential Equations, 46, 879-889. [Google Scholar] [CrossRef] 
[7] Cheng, Q.M. and Peng, Y.J. (2015) Complete Self-Shrinkers of the Mean Curvature Flow. Calculus of Variations and Partial Differential Equations, 52, 497-506. [Google Scholar] [CrossRef] 
[8] Cao, S.J., Xu, H.W. and Zhao, E.T. (2014) Pinching Theorems for Self-Shrinkers of Higher Codimension. Preprint.
[9] Cheng, Q.M. and Wei, G.X. (2015) A Gap Theorem of Self-Shrinkers. Transactions of the American Mathematical Society, 367, 4895-4915. [Google Scholar] [CrossRef] 
[10] Ding, Q. and Xin, Y.L. (2014) The Rigidity Theorems of Self-Shrinkers. Transactions of the American Mathematical Society, 366, 5067-5085. [Google Scholar] [CrossRef] 

为你推荐