SiO₂网络结构的分子模拟及玻璃化研究

Molecular Simulation and Vitrification of SiO₂ Network Structure

摘要: 玻璃是一种无序的材料，缺乏晶体的周期性，但在机械性能上类似固体。制作玻璃最常见的方法是快速冷却粘性液体以避免结晶，尽管冷却获得玻璃这一方法已为人们所熟知，但从液体转变成无定型刚性结构这一过程的微观机理还尚未被人们完全理解。经典分子动力学模拟作为一种研究物质微观结构的有效手段，能够提供关于非晶材料静态结构和动态特性的详细信息，为研究玻璃结构提供了科学可行的方法。在本工作中，我们针对以往玻璃分子动力学模拟中无拓扑定义力场对高温和常温下物理性质描述无法兼顾的难题，提出了一种变温拓扑构造方法，在不同的温度下构建不同的SiO₂无规网络拓扑结构用于熔体冷却玻璃化过程的分子动力学模拟。分析了熔体冷却玻璃化过程中的结构性质、动力学性质与热力学性质变化，我们发现变温拓扑构造方法能准确描述SiO₂玻璃化过程中径向分布函数、体积、扩散系数、松弛时间等结构性质和动力学性质，并且对动力学与热力学关系的描述符合Adam-Gibbs理论，得到的协作重排区域尺寸在熔体冷却玻璃化过程中逐渐减小。

Abstract: Glass is an amorphous material which lacks the periodicity of crystals and behaves as solid in mechanical properties. The most common method to make glass is cooling the viscous liquid quickly to avoid crystallization. Although the method of obtaining glass by cooling is well known, the microscopic mechanism of the transition from liquid to amorphous rigid structure is not fully understood. As an effective means to study the microstructure of materials, classical molecular dynamics simulation can provide detailed information about the static structure and dynamic characteristics of amorphous materials and give the scientific and feasible method for the study of glass structure. In this work, we aim at the problem that the same force field cannot describe the physical properties at high temperature and normal temperature in the previous glass molecular dynamics simulation simultaneously. A method of topological construction of variable temperature was proposed by us, and various topological structures of SiO₂ random network were obtained at different temperatures for molecular dynamics simulation of melt cooling vitrification process. The changes of structural properties, kinetic properties and thermodynamic properties in melt cooling vitrification process were analyzed. It is found that the variable temperature topological construction method can accurately describe the variation law of structural properties and dynamic properties such as radial distribution function, volume, diffusion coefficient and relaxation time with temperature in SiO₂ vitrification process, and the description of the relationship between dynamics and thermodynamics in vitrification conforms to Adam-Gibbs theory.

1. 引言

硅基玻璃的结构可以看作由Si元素构成基本骨架的连续随机网络 [1]，并且网络拓扑结构(原子的键接关系)受多种因素影响，比如温度、压力和制备条件。玻璃的化学组成和化学计量比也会导致网络拓扑差异，例如，BeCl₂、GeSe₂、GeO₂等玻璃系统(在环境压力下)与SiO₂有类似的化学计量比，所以它们的网络拓扑结构都是由[MX4]类型的四面体(CP)构成的，关键区别在于相邻四面体之间的角度(由桥接阴离子的极化率控制) [2]，四面体相连接的拓扑结构导致在这一类网络在多个空间尺度上存在着有序结构(短程有序和中程有序)，而温度和压力等环境因素通过改变CP间的连接角度和CP自身的几何结构(例如高压下原子近邻的配位数增多)来改变网络拓扑 [3] [4] [5]。这种网络拓扑随温度或压力变化的现象是玻璃结构的重要特征，对于液体的玻璃化研究有重要意义。

石英玻璃中的Si-O键兼具共价键与离子键成分，选择合适的力场与构建合理的初始结构是石英玻璃分子动力学模拟的关键。在以往的玻璃体系分子模拟工作中，大多是在确定好力场后，使用对应的晶体作为初始结构，在高温下平衡熔融得到液体结构，最终通过降温退火模拟得到玻璃结构 [6] [7] [8]。这一类方法中使用的势函数没有拓扑的定义，比如在Tersoff [7] 多体势中引入了键级函数，通过原子间距离判断化学键的强弱，原子周围的配位情况由键级大小判定；或是直接以非对称的离子型对势(FB [9], TTAM [10], Morse [11] )描述所有原子对的相互作用 [12]。玻璃在高温与常温下的结构性质表现出巨大差异，化学键的断裂与重连导致网络拓扑重构，从而改变势能面形貌 [13] [14] [15]。所以无拓扑定义的力场通常无法描述玻璃随温度变化的结构性质，比如多体势能较好地描述常温下石英玻璃中[SiO₄]四面体结构以及四面体间形成的中程序结构 [16] [17] [18]，但多原子约束作用使其不能描述高温下Si-O键的断裂与体积变化的不规则性，不利于高温下离子迁移扩散等运输性质的研究；离子型对势能很好地描述高温下Si-O键的断裂 [7] [19] [20]，可以模拟高温下的离子迁移与扩散过程，但由于势函数中缺少键角能项，无法描述常温下[SiO₄]四面体的对称结构。所以无拓扑定义的力场对玻璃高温和常温下物理性质的描述通常是难以兼顾的，这一问题主要来源于玻璃在高温和常温下拓扑的明显差异，如高温下化学键断裂形成稀疏网络并伴随着[SiO₄]四面体对称性破坏，低温下体积收缩形成的紧密网络与稳定的[SiO₄]四面体结构。因此利用含拓扑定义的力场描述随温度变化的网络结构中原子间相互作用，可以体现玻璃在不同温度下的结构差异，并有可能准确描述熔体冷却玻璃化过程中的热力学变化规律。

在本工作中，提出了一种变温拓扑构造的方法，在不同的温度下得到不同的SiO₂无规网络拓扑结构用于熔体冷却玻璃化过程的分子动力学模拟。并验证这种变温拓扑构造方法应用在玻璃分子动力学模拟中的科学性与可行性。

2. 模拟方法

2.1. SiO₂液体冷却退火模拟

离子型对势能很好地描述玻璃熔体中原子的迁移扩散过程，我们使用Ersan Demiralp等人 [21] 提出的离子型对势Morse-Stretch势函数模拟SiO₂熔体冷却退火过程，该势函数包含了非静电相互作用(短程泡利斥力、色散力、共价力等)，其形式如下：

$U_{MS}\left(R\right)=D_0\left({\text{e}}^{\gamma \left(1-R/R_0\right)}-2{\text{e}}^{\left(\gamma /2\right)\left(1-R/R_0\right)}\right)$ (1)

其中， $D_0$ 为势阱深度， $\gamma$ 是与势作用宽度相关的参数， $R_0$ 对应原子间作用的平衡距离。SiO₂玻璃的MS势参数如表1所示。

Table 1. Morse-Stretch potential parameter of SiO2 glass

表1. SiO₂玻璃的Morse-stretch势参数

如图1(a)，为α_SiO₂晶胞在xyz三个方向上扩胞后得到3.28 nm × 3.28 nm × 3.28 nm的超胞，以该超胞作为初始结构，用表1中的Morse-Stretch势参数描述原子间相互作用，将晶体结构从300 K升温至3000 K进行10 ns的NPT模拟，随后在3000 K下作10 ns的NPT平衡模拟得到SiO₂的熔体结构，熔体密度为1.87 g/cm³。最后将熔体SiO₂从3000 K降温至到300 K进行20 ns的退火模拟。

2.2. 网络拓扑结构构建

在300~3000 K温度范围抽取18个退火点温度下的结构，以0.2 nm为截断距离判断Si-O键的形成，构造不同退火温度下的网络拓扑，用含拓扑定义的OPLS力场描述网络结构中原子的相互作用。

$\begin{array}{c}E={\displaystyle \underset{bonds}{\sum }{K}_r{\left(r-r_0\right)}^2}+{\displaystyle \underset{angles}{\sum }{K}_{\theta }{\left(\theta -{\theta }_0\right)}^2}+{\displaystyle \underset{dihedrals,n}{\sum }\frac{V_n}{2}\left[1+\cos \left(n\varphi -{\varphi }_0\right)\right]}\\ +{\displaystyle \underset{i>j}{\sum }{f}_{ij}\left(\frac{A_{ij}}{r_{ij}^{12}}-\frac{C_{ij}}{r_{ij}^6}+\frac{q_i{q}_j{e}^2}{4\pi {\epsilon }_0{r}_{ij}}\right)}\end{array}$ (2)

方程(2)为OPLS力场中的势函数，等号右侧的项分别对应键伸缩势、键角弯曲势、二面角扭转势与非键作用势。将网络结构分别在对应温度下作10 ns的NPT平衡模拟与10 ns的NPT平衡采样。如图1(b)，得到了300 K下的SiO₂玻璃结构，密度为2.34 g/cm³，与实验值相近。

(a) (b)

Figure 1. (a) Crystal structure of SiO₂; (b) glass structure of SiO₂

图1. (a) α_SiO₂晶体结构；(b) SiO₂玻璃结构

3. 结果与讨论

3.1. 结构性质

计算了不同温度下的径向分布函数，如图2，随着温度降低，各个原子对的径向分布图中第一峰和第二峰(0~1 nm)的强度明显增大，说明冷却过程中体系短程序与中程序增多。另外在Si-O的径向分布图中，温度降至1700 K左右第一峰位置向左移动，温度降至1700 K以下，峰位置不再有明显变化，说明该温度下自由体积已降至最小，体系可能发生了玻璃化转变。

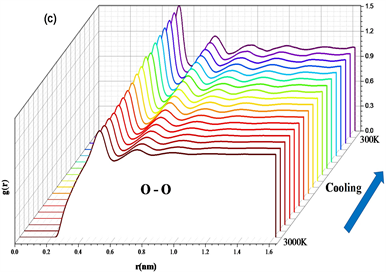
Figure 2. (a) RDF of Si-O atomic pair; (b) RDF of Si-Si atomic pair; (c) RDF of O-O atomic pair

图2. (a) Si-O原子对径向分布函数；(b) Si-Si原子对径向分布函数；(c) O-O原子对径向分布函数

如图3，从温度体积–曲线可以看出熔体冷却过程中伴随着Si-O键的形成，网络密度逐渐增大，体积收缩，并在1640 K左右出现了玻璃化转变，与径向分布函数的结果一致。以上结果表明变温拓扑构造方法能很好地描述SiO₂熔体冷却玻璃化过程的结构性质变化。

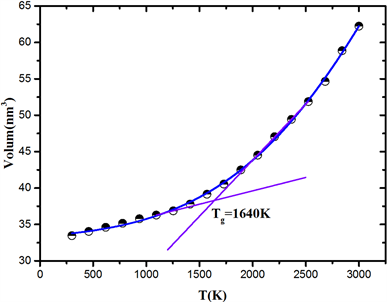
Figure 3. Volume-Temperature curve during melt cooling process

图3. 熔体冷却过程的体积–温度曲线

3.2. 动力学性质

为研究熔体冷却玻璃化过程中的动力学变化行为，我们计算了不同温度下的扩散系数与松弛时间。如图4(a)，从MSD随时间的变化曲线可以看出，高温下大量化学键断裂形成稀疏的网络结构使得原子表现出类似于液体中扩散行为，而低温下则表现出固体中原子的扩散行为。通过拟合均方位移MSD-时间曲线得到扩散系数D_A：

${\lim }_{t\to \infty }{\langle {\Vert r_i\left(t\right)-r_i\left(0\right)\Vert }^2\rangle }_{i\in A}=6D_{A}t$ (3)

如图4(b)，在SiO₂熔体冷却至玻璃化温度T_g前，原子的自扩散系数急剧降低，当温度冷却至T_g时，自扩散系数减小了4个数量级，此时体系发生了严重的动力学粘滞现象。

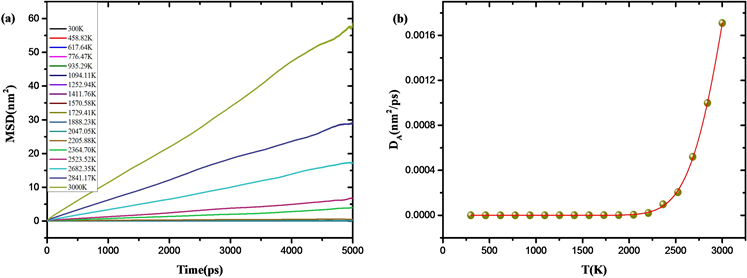
Figure 4. (a) MSD-time curve at different temperature; (b) The diffusion coefficient varies with temperature

图4. (a) 不同温度下均方位移(MSD)随时间变化曲线；(b) 扩散系数随温度变化图

用二面角自相关函数(TACF)表达体系的结构松弛：

$C\left(t\right)=\langle \cos \left[\phi \left(t\right)-\phi \left(0\right)\right]\rangle$ (4)

通过Kohlrausch-Williams-Watts (KWW)方程 [22] [23] [24] 拟合自相关系数随时间的变化关系：

$C\left(t\right)={\text{e}}^{-{\left(\frac{t}{\tau }\right)}^{\beta }}$ (5)

如图5(a)，为300 K下二面角自相关系数 $C\left(t\right)$ 随时间变化的拟合曲线，其中拟合参数 $\beta <\text{1}$，表明了玻璃结构中的非指数弛豫行为 [25] [26] [27]，拟合参数 $\tau$ 为特征松弛时间。将拟合参数 $\tau$ 与 $\beta$ 带入Gama函数求解得到体系的松弛时间 ${\tau }_{inf}$。

${\tau }_{inf}={\displaystyle {\int }_0^{\infty }{\text{e}}^{-{\left(\frac{t}{\tau }\right)}^{\beta }}\text{d}t}=\frac{\tau }{\beta }\Gamma \left(\frac{1}{\beta }\right)$ (6)

如图5(b)，从T_g标度的松弛时间–温度图中可以看出由变温拓扑构造方法得到的玻璃松弛时间随温度变化符合Arrhenius关系，表明SiO₂具有强液体结构。

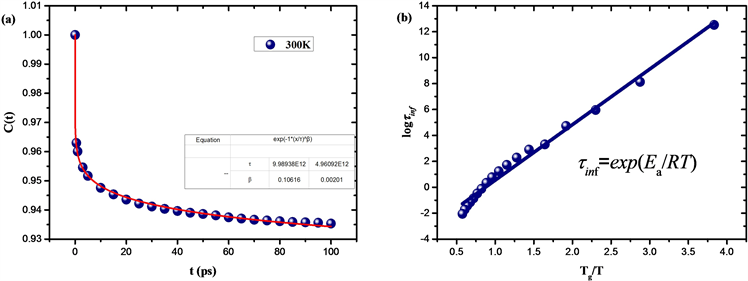
Figure 5. (a) The fitting curve of dihedral Angle autocorrelation coefficient changing with time at 300 K; (b) Relaxation time-temperature curve of T_g scale

图5. (a) 300 K下二面角自相关系数随时间变化的拟合曲线；(b) T_g标度的松弛时间–温度变化曲线

3.3. 热力学性质

在上文的内容中我们验证了变温拓扑构造方法用于分析SiO₂熔体冷却玻璃化过程中结构性质、运输性质和动力学性质的可行性，为研究液体冷却玻璃化过程的热力学变化，我们对不同温度下体系运动轨迹进行简正振动分析，并根据Schlitter公式 [28] 计算了SiO₂熔体冷却过程中的液体熵 $S_{liquid}$ 以及相应温度下的晶体熵 $S_{crystal}$。

$S=\frac{1}{2}{k}_B\ln \left[\det \left(E+\frac{4{\pi }^2{k}_{B}T{e}^2}{h^2}M\sigma \right)\right]$ (7)

其中M为质量加权矩阵， $\sigma$ 为原子坐标的协方差矩阵，E为单位矩阵，h为普朗克常量。如图6(a)，从液体熵和晶体熵随温度的变化图可以看出，液体在熔化温度T_m下的熵高于相应晶体的熵，由于液体的热容比晶体高，这种熵差在过冷时减小。拟合T_g以上的液体熵曲线并向低温区外推相交于晶体熵曲线，得到了SiO₂液体的Kauzmann温度T_K = 1300 K。

计算了以熔融熵标度的剩余熵 $\Delta S/\Delta S_m$，其中 $\Delta S=S_{liquid}-S_{crystal}$，熔融熵 $\Delta S_m=\Delta S\left(T_m\right)$。如图6(b)，以 $\Delta S/\Delta S_m$ 对T/T_m作图，可以看出在温度降至Kauzmann温度前玻璃化转变的介入避免了剩余熵在非零温度下归零，这表明玻璃的动力学和热力学之间存在着联系。从该分析中产生的热力学观点认为，实验室的玻璃化转变是一种向理想玻璃发生基本热力学转变的动力学控制。因此变温拓扑构造方法除了对玻璃转变动力学有很好的描述，也准确反映了液体冷却玻璃化过程的热力学变化，对剩余熵与温度变化关系的描述也符合玻璃化转变的热力学观点 [29]。

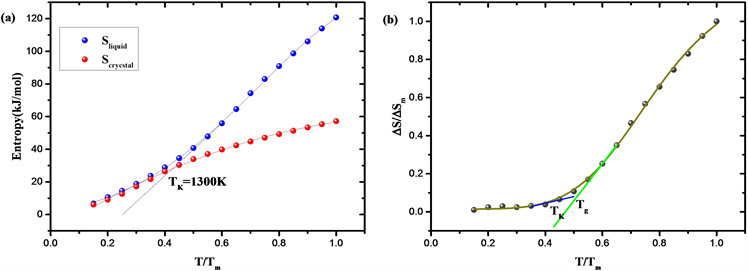
Figure 6. (a) Entropy of SiO₂ liquid and entropy of SiO₂ crystal changing with temperature; (b) Residual entropy-temperature curve with T_m scale

图6. (a) SiO₂液体熵与晶体熵随温度变化图；(b) T_m标度的剩余熵-温度图

除了动力学与热力学变化外，在玻璃转变的研究中我们往往对动力学与热力学之间的联系更感兴趣。Adam、Gibss等人 [30] 在玻璃转变的动力学和热力学之间提供了一种启发性的联系，即Adam-Gibbs模型 ${\tau }_{inf}=A\exp \left(C/T{S}_c\right)$，它描述了体系的构型熵 $S_c$ 与松弛时间 ${\tau }_{inf}$ 的数量关系。我们计算了SiO₂玻璃网络的构型熵 $S_c$，并结合上文中的松弛时间 ${\tau }_{inf}$ 来验证变温拓扑构造方法对玻璃化过程的描述是否符合Adam-Gibbs模型，由于构型熵的计算需要采样大量的构型，以目前的计算机水平无法实现，所以在这里我们使用键渗透模型对构型熵进行估算 [31]。根据一维渗透模型，通过SiO₂熔体冷却过程中不同温度下的网络密度p估算构型熵 $S_c$ ：

$S_c=\left(1-p\right)S_c^0$ (8)

其中p为网络密度，即网络中的Si-O键数目N_bond与4倍Si原子总数4N_Si的比值p = N_bond/4N_Si， $S_c^0$ 对应熔体的构型熵。将上式带入上述的Adam-Gibbs模型得到：

${\tau }_{inf}=A\exp \left[\frac{B/S_c^0}{\left(1-p\right)T}\right]$ (9)

在方程(9)中，A、B、 $S_c^0$ 是与网络密度p无关的常数，如图7，利用方程(9)拟合了松弛时间 $\ln {\tau }_{inf}$ 与 $\left(1-p\right)T$ 之间的关系，可以看出变温拓扑构造方法对松弛时间与构型熵之间的关系描述与Adam-Gibbs模型相符，能够准确描述玻璃化过程中动力学与热力学之间的关系。由于Adam-Gibbs模型的推导中引入协作重排子系统概念，体系的构型熵与协作重排子系统中的粒子数目有关，而在以往的无拓扑定义的玻璃分子动力学模拟中，仅依靠降温过程限制体系构型无法体现原子间的协同运动关系，因而难以得到符合Adam-Gibbs模型的计算结果。

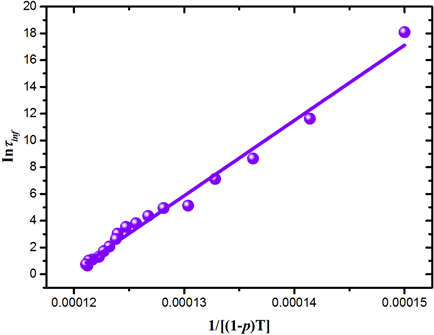
Figure 7. The curve of relaxation time changing with network density

图7. 松弛时间随网络密度的变化图

在推导AG模型时，Adam和Gibbs引入了协作重排区域(CRR)的概念，但他们推导过程的一个缺陷是没有提供关于这些区域大小的信息与计算方法，在下面的内容中我们根据Trap模型 [32] 结合自由能面(Free energy landscape)结构研究了温度对CRR尺寸的影响。

3.4. 协作重排区域尺寸(CRR)

协作重排区域(CRR)是由Adam和Gibbs提出的用于理解玻璃化转变的重要概念。在他们的理论中，结构弛豫是由CRR中的粒子重排引起的。后来Takashi Yoshidome等人 [33] [34] [35] 将CRR与自由能面联系起来并给出了CRR的微观定义。即在自由能面上，结构弛豫对应了从一个盆地到邻近盆地的过渡，并且该过程中所涉及的粒子不是系统中的全体粒子，而是某些粒子，这些粒子被认为是CRR中的粒子，同时也是处于两个相邻盆地之间的激发态上的协同运动粒子。所以根据Takashi Yoshidome等人的观点，可以直接从自由能面的结构中得到CRR中粒子数，但他们的工作是利用介观密度泛函理论方法对硬球粒子模型组成的玻璃结构进行自由能最小化等到自由能面，无法体现结构弛豫的真实动力学过程。在本工作中，我们利用Metadynamics [36] 方法构建SiO₂玻璃结构的自由能面，并从自由能面结构中判断CRR中的粒子数。

如图8，根据Trap [37] 模型，将体系中的部分原子限制在球形区域(以下称为Trap区域)内运动，并将区域外的原子位置冻结。通过不断调整Trap区域的半径 $r_{Trap}$ 寻找能使区域内原子发生协作重排的最小半径 $r_{CRR}^{*}$。

对Trap区域内的体系进行二面角主成分分析dihedral PCA [38] (下面简称dPCA)得到体系运动的特征方向，并将轨迹投影在特征方向上得到主模。将dPCA分析中协方差矩阵最大的两个特征值所对应的特征向量记为e₁、e₂。轨迹在e₁、e₂上的投影记为PCA-1、PCA-2。以PCA-1、PCA-2作为集中变量(collective variables)CVs进行Metadynamics增强采样 [39] 得到沿着集中变量方向上的自由能面。

Figure 8. Trap model

图8. Trap模型示意图

将 $r_{Trap}^2$ 以0.01 nm²的步长逐步缩小，当自由能面上出现相邻盆地之间相互转化的鞍点时，便认为Trap区域内的原子发生了协作重排，即 $r_{Trap}>r_{CRR}^{*}$。反之 $r_{Trap}<r_{CRR}^{*}$。

如图9，为935 K温度下 $r_{Trap}$ 分别为0.5292 nm、0.5385 nm、0.5441 nm、0.5450 nm所对应的自由能面。可以看出 $r_{Trap}\le 0.5385\text{nm}$ 时，Trap区域内原子没有发生协作重排(自由能面上无鞍点)，而 $r_{Trap}\ge 0.5441\text{nm}$ 时，Trap区域内原子发生了协作重排，于是我们认为935K温度下体系的协作重排区域最小尺寸 $r_{CRR}^{*}$ 为0.5441 nm，得到区域内原子数 $N_{atoms}^{*}$ 为45。

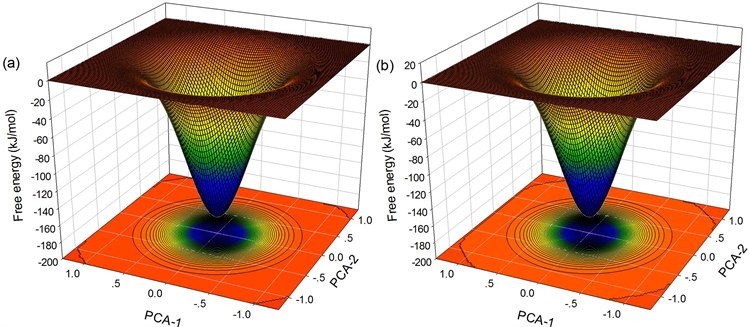
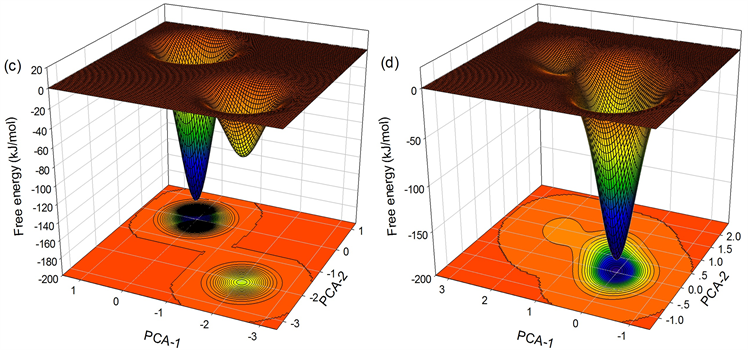
Figure 9. Free energy landscape with (a) $r_{Trap}=0.5292\text{nm}$ ; (b) $r_{Trap}=0.5385\text{nm}$ ; (c) $r_{Trap}=0.5441\text{nm}$ ; (d) $r_{Trap}=0.5450\text{nm}$

图9. 935 K温度下Trap区域半径分别为(a) $r_{Trap}=0.5292\text{nm}$ ；(b) $r_{Trap}=0.5385\text{nm}$ ；(c) $r_{Trap}=0.5441\text{nm}$ ；(d) $r_{Trap}=0.5450\text{nm}$ 所对应的自由能面

将集中变量CVs对时间作图以观察协作重排动态过程。如图10，为935 K温度下 $r_{Trap}=0.5450\text{nm}$ 的体系中CVs随模拟时间的变化图，可以看出，体系初始状态对应CVs = 0附近的盆地，在模拟的前200 ps内体系状态处于该盆地中。200 ps后体系采样勘测到近邻盆地，此时CRR内的原子越过能垒发生协作重排，随后在两个盆地间来回作构象跃迁。

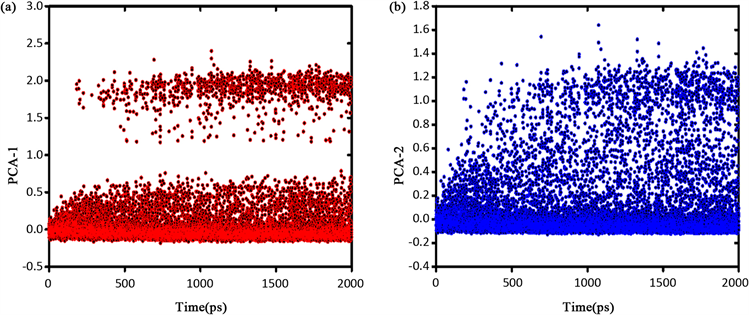
Figure 10. (a) Collective variable PCA-1 changing with time; (b) Collective variable PCA-2 changing with time

图10. (a) 集中变量PCA-1随时间变化图；(b) 集中变量PCA-2随时间变化图

按照上述方法计算了熔体冷却过程中的5个退火温度下CRR的最小尺寸 $r_{CRR}^{*}$ 和CRR中的原子数 $N_{atoms}^{*}$。如图11，可以看出，CRR最小尺寸以及其中的原子数随着温度的降低而增加，说明冷却过程中系统构型采样数量减少导致了原子的协同运动加剧，从而增大了协作重排尺寸。

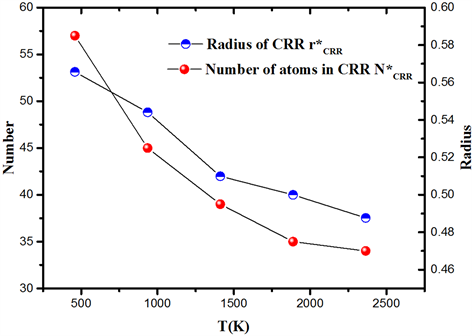
Figure 11. Number of atoms in CRR and minimum size of CRR at different temperature

图11. CRR中的原子数 $N_{atoms}^{*}$ 和CRR最小尺寸 $r_{CRR}^{*}$ 随温度的变化图

4. 总结

在本工作中，我们首先用离子型对势(Morse-Strench势)描述SiO₂熔体中的原子相互作用，通过在Si-O原子间设置截断距离得到各个退火点温度下的无规网络拓扑。用含有拓扑定义的力场描述网络结构中原子相互作用，研究了SiO₂熔体冷却玻璃化过程中的结构性质、动力学性质与热力学性质随温度的变化规律，验证了这种变温拓扑构造方法应用在玻璃分子动力学模拟中的科学性与可行性。我们得到了以下结论：

1) 变温拓扑构造方法能很好地描述SiO₂熔体冷却玻璃化过程中的结构性质变化，得到的扩散系数在Tg前后有数量级的变化，松弛时间与温度表现Arrhenius行为，符合SiO₂强液体结构。

2) SiO₂熔体在降至Kauzmann温度前玻璃化转变介入避免了剩余熵在非零温度下归零，表明玻璃化转变的动力学和热力学之间存在着联系，得到的构型熵与松弛时间符合Adam-Gibbs理论模型，变温拓扑构造方法能够准确描述玻璃化过程中动力学与热力学之间的关系。

3) SiO₂熔体冷却过程中协作重排区域(CRR)尺寸不断减小，表明冷却过程中系统构型采样数量减少导致了原子的协同运动加剧，从而增大了协作重排尺寸。