含Euler函数的非线性不定方程φ(mn)=aφ(m)+bφ(n)+c的解的个数及范围

The Number and Range of the Solutions of the Nonlinear Diophantine Equation φ(mn)=aφ(m)+bφ(n)+c with Euler Function

摘要: Euler函数φ(n)是数论中一个非常重要的函数，本文主要讨论了非线性不定方程φ(mn)=aφ(m)+bφ(n)+c解数(即正整数解的个数)有限的充要条件和此时解的范围。从而对给定的系数a，b，c，当不定方程解数有限时，我们在给定的范围内通过计算机穷举给出方程的所有正整数解。

Abstract: Euler function φ(n) is a very important function in number theory. In this paper, we mainly discuss the necessary and sufficient conditions for the nonlinear Diophantine equation φ(mn)=aφ(m)+bφ(n)+c which has the finite number of positive integer solutions and the range of solutions whenever the number of solutions is limited. Therefore, for a given coefficient a, b, c, searching a given range by a computer, we can give all the positive integer solutions of the equation when the number of solutions is limited.

1. 引言

对任意正整数n，令 $\phi \left(n\right)$ 为Euler函数，即在正整数1到n中与n互素的整数的个数。Euler函数是数论中一个非常重要的函数，有关 $\phi \left(n\right)$ 方程解的研究有很多，得到了不少有趣的结论。如文献 [1] - [7] 讨论了方程 $\phi \left(mn\right)=k\left(\phi \left(m\right)+\phi \left(n\right)\right)$ 当 $k=3,4,6,7,8,10,11,15$ 时所有的正整数解；文献 [8] [9] 讨论了方程 $\phi \left(mn\right)=a\phi \left(m\right)+b\phi \left(n\right)$ 当 $\left(a,b\right)=\left(7,9\right),\left(15,17\right)$ 时的所有正整数解；文献 [10] [11] [12] 讨论了方程 $\phi \left(mn\right)=a\phi \left(m\right)+b\phi \left(n\right)+c$，当 $\left(a,b,c\right)=\left(5,6,16\right),\left(7,8,16\right),\left(9,16,24\right)$ 时的所有整数解；文献 [13] 中研究了当b为奇数时，方程 $\phi \left(mn\right)=k_1\phi \left(m\right)+k_2\phi \left(n\right)+b$ 在有解的情况下 $k_1,k_2,b$ 需要满足的条件，并举例给出了方程 $\phi \left(mn\right)=4\phi \left(m\right)+7\phi \left(n\right)+8$ 的所有正整数解。然而目前的研究主要集中在对于具体给定的一组系数或满足一些特殊条件的一类系数组，求出方程 $\phi \left(mn\right)=a\phi \left(m\right)+b\phi \left(n\right)+c$ 的所有整数解方面，很少考虑到该方程一般情形下的解数及解的范围问题。

本文主要讨论了方程 $\phi \left(mn\right)=a\phi \left(m\right)+b\phi \left(n\right)+c$ 解数(即正整数解的个数)有限的充要条件和此时解的范围。从而对给定的系数 $a,b,c$，我们可用计算机在给定的范围内穷举相应方程的所有正整数解。第一节给出了一些相关引理，第二节给出我们的主要定理，第三节给出了一些算例。

2. 相关引理

在本节中我们给出一些Euler函数 $\phi \left(n\right)$ 的基本性质。文中提到但未定义的一些概念和未引用的基本结论可以在教材 [14] 或手册 [15] 中找到。

引理2.1 [16] 对任意正整数m和n，若 $m|n$，则 $\phi \left(m\right)|\phi \left(n\right)$。

引理2.2 [16] 对任意正整数m和n，则 $\phi \left(mn\right)=\frac{gcd\left(m,n\right)\phi \left(m\right)\phi \left(n\right)}{\phi \left(gcd\left(m,n\right)\right)}$。特别当 $\gcd \left(m,n\right)=1$ 时， $\phi \left(mn\right)=\phi \left(m\right)\phi \left(n\right)$。其中 $\gcd \left(m,n\right)$ 表示m和n的最大公约数。

引理2.3 [16] 当 $n\ge 2$ 时， $\phi \left(n\right)<n$。当 $n\ge 3$ 时， $\phi \left(n\right)$ 必为偶数。

引理2.4 [15] 对于任意的除了2和6的正整数n，则 $\phi \left(n\right)\ge \sqrt{n}$。

推论2.5 对于任意的正整数n，满足 $n\le {\phi }^2\left(n\right)+2$。

证明：由引理2.4可得对于任意的除了2和6的正整数n，则 $\phi {\left(n\right)}^2\ge n$。因为 $\phi \left(2\right)=1,\phi \left(6\right)=2$，所以 $\phi {\left(2\right)}^2=1,\phi {\left(6\right)}^2=4$，所以结论成立。■

引理2.6 [15] 对于任意的正整数n，当 $n>42$ 时， $\phi \left(n\right)>n^{2/3}$。

在文献 [15] 第九页中的第2个公式 $\phi \left(n\right)>n^{2/3}$ for $n>30$，通过计算机的有限穷举后发现当 $n=42$ 时不满足这个不等式，所以不等式 $\phi \left(n\right)>n^{2/3}$ 满足的条件是 $n>42$。

推论2.7 对于任意的正整数n，则 $n<{\phi }^{3/2}\left(n\right)+8$。

证明：由引理2.6可得，对于任意的正整数n，当 $n>42$ 时， $n<\phi {\left(n\right)}^{3/2}$。我们用计算机穷举当 $n\le 42$ 时， $\phi {\left(n\right)}^{3/2}$ 的所有值，并且得到对于任意的正整数n， $n<{\phi }^{3/2}\left(n\right)+8$ 都成立。■

由推论2.5或推论2.7，我们易得：

定理2.8 对于给定的正整数d，方程 $\phi \left(n\right)=d$ 的解数有限。

根据引理2.3，对所有大于1的奇数d，方程 $\phi \left(n\right)=d$ 无解。而d为正偶数时，方程 $\phi \left(n\right)=d$ 也未必有解。根据推论2.7，我们通过用数学软件Mathematica穷举得知，在10,000 (含)以内使方程 $\phi \left(n\right)=d$ 有解的(/无解的)正偶数d有2373 (/2627)个。此处我们仅列举500 (含)以内使方程 $\phi \left(n\right)=d$ 无解的93个正偶数d：14，26，34，38，50，62，68，74，76，86，90，94，98，114，118，122，124，134，142，146，152，154，158，170，174，182，186，188，194，202，206，214，218，230，234，236，242，244，246，248，254，258，266，274，278，284，286，290，298，302，304，308，314，318，322，326，334，338，340，350，354，362，364，370，374，376，386，390，394，398，402，404，406，410，412，414，422，426，428，434，436，446，450，454，458，470，472，474，482，484，488，494，496。

3. 定理及其证明

本节我们考察下述方程

$\phi \left(mn\right)=a\phi \left(m\right)+b\phi \left(n\right)+c$ (1)

的解数及解数有限时解的范围。

引理3.1 若不存在正整数d，满足 $\phi \left(d\right)|c$，且 $\frac{cd}{\phi \left(d\right)}+ab=0$，则方程(1)的解数有限。

证明：设正整数对 $\left(m,n\right)$ 是方程(1)的任一组解(若方程无解，则结论显然成立)。此时记 $d=gcd\left(m,n\right)$，则由引理2.1知，必存在 $m_1,n_1\in Z^{+}$，使 $\phi \left(m\right)=m_1\phi \left(d\right)$， $\phi \left(n\right)=n_1\phi \left(d\right)$。再由引理2.2，方程(1)可化为

$\phi \left(d\right)\left(d{m}_1{n}_1-a{m}_1-b{n}_1\right)=c,$

从而有 $\phi \left(d\right)|c$ 且 $\left(d{m}_1{n}_1-a{m}_1-b{n}_1\right)|c$。设 $c_1=\frac{c}{\phi \left(d\right)}$，则上述方程可继续化简为

$d{m}_1{n}_1-a{m}_1-b{n}_1=c_1,$ (2)

方程两边同时乘以d后再加上ab，方程进一步可化为

$\left(d{m}_1-b\right)\left(d{n}_1-a\right)=c_{1}d+ab.$ (3)

此时必有 $d{m}_1-b|c_{1}d+ad,d{n}_1-a|c_{1}d+ad$。再由题设知 $c_{1}d+ab=\frac{c}{\phi \left(d\right)}d+ab\ne 0$，则其因子对必有限，故满足条件的正整数对 $\left(m_1,n_1\right)$ ——方程(3)的解数——必有限(因对于给定的因子对得到的 $m_1,n_1$ 可能不是正整数，故数量可能会更少)。又当 $c\ne 0$ 时， $\phi \left(d\right)|c$，而当 $c=0$ 时方程(2)化简得 $d=\frac{a}{n_1}+\frac{b}{m_1}\le \left|a\right|+\left|b\right|$，因而可能的 $\phi \left(d\right)$ 的取值只有有限个。因此正整数对 $\left(\phi \left(m\right),\phi \left(n\right)\right)=\left(m_1,n_1\right)\phi \left(d\right)$ 必是有限的。最后由定理2.8知，方程(1)的解组 $\left(m,n\right)$ (满足 $\left(\phi \left(m\right),\phi \left(n\right)\right)=\left(m_1,n_1\right)\phi \left(d\right)$ )必是有限的(可能无解)。■

引理3.2 方程(1)的解数无限当且仅当存在正整数d，使得 $\phi \left(d\right)|c,\frac{cd}{\phi \left(d\right)}+ab=0$，且方程 $\phi \left(m\right)=\frac{b\phi \left(d\right)}{d}\left(d|m\right)$ 或 $\phi \left(n\right)=\frac{a\phi \left(d\right)}{d}\left(d|n\right)$ 有正整数解。

证明：必要性。设方程(1)有无穷多解，并任取其一解 $\left(m,n\right)$。在与引理3.1的证明完全相同的记号和讨论下知，此时必有 $c_{1}d+ab=\frac{c}{\phi \left(d\right)}d+ab=0$。从而方程(3)化为

$\left(d{m}_1-b\right)\left(d{n}_1-a\right)=0.$ (4)

因而 $d{m}_1-b=0$ 或 $d{n}_1-a=0$。故 $m_1=\frac{b}{d}$ 为正整数或 $n_1=\frac{a}{d}$ 为正整数。因此有 $\phi \left(m\right)=m_1\phi \left(d\right)=\frac{b\phi \left(d\right)}{d}$ 或 $\phi \left(n\right)=n_1\phi \left(d\right)=\frac{a\phi \left(d\right)}{d}$。结论成立。

充分性。设存在正整数d，使得 $\phi \left(d\right)|c,\frac{cd}{\phi \left(d\right)}+ab=0$，且不妨设正整数m满足条件 $\phi \left(m\right)=\frac{b\phi \left(d\right)}{d},d|m$。则易知对任意满足条件 $\gcd \left(m,n\right)=d$ 的正整数n (显然有无穷多个)，正整数对 $\left(m_1,n_1\right)=\left(\frac{\phi \left(m\right)}{\phi \left(d\right)},\frac{\phi \left(n\right)}{\phi \left(d\right)}\right)$ 是方程(4)的解，从而正整数对 $\left(m,n\right)$ 都是方程(1)的解(无穷多个)。

由引理3.1和引理3.2，我们可得到本节第一个主要结论。

定理3.3 方程(1)的解数有限当且仅当不存在正整数d，使得 $\phi \left(d\right)|c,\frac{cd}{\phi \left(d\right)}+ab=0$，且方程 $\phi \left(m\right)=\frac{b\phi \left(d\right)}{d}\left(d|m\right)$ 或 $\phi \left(n\right)=\frac{a\phi \left(d\right)}{d}\left(d|n\right)$ 有正整数解。■

下面我们进一步讨论当方程(1)的解数有限时，其解的范围。

定理3.4 当方程(1)解数有限时，其解的范围为：

$m\in \left[1,{\left(\left|c\right|+\left|ab\right|+\left|b\right|\right)}^{3/2}+8\right],n\in \left[1,{\left(\left|c\right|+\left|ab\right|+\left|a\right|\right)}^{3/2}+8\right].$

证明：根据常数c是否为0，我们分两种情形讨论。

情形1： $c=0$。由定理3.3知，必有 $ab\ne 0$。

此时记 $d=gcd\left(m,n\right)$，则方程(1)化为

$d{m}_1{n}_1-a{m}_1-b{n}_1=0.$ (5)

两边同时乘以d化简为：

$\left(d{m}_1-b\right)\left(d{n}_1-a\right)=ab.$ (6)

当 $a<0,b<0$ 时，由欧拉函数的定义可知方程(1)无解。

当 $a>0,b<0$ 或 $a<0,b>0$ 时。由方程(6)可知，当 $d{n}_1-a=-1$ 时， $m_1=\frac{-ab+b}{d}$，由 $\phi \left(m\right)=m_1\phi \left(d\right)$， 得 $\phi \left(m\right)=\frac{\phi \left(d\right)\left(-ab+b\right)}{d}\le \left|ab\right|+\left|b\right|$，由推论2.7得 $m\in \left[1,{\left(\left|ab\right|+\left|b\right|\right)}^{3/2}+8\right]$。同理可得 $n\in \left[1,{\left(\left|ab\right|+\left|b\right|\right)}^{3/2}+8\right]$

当 $a>0,b>0$ 时。在方程(6)中，当 $d{n}_1-a=1$ 时， $m_1=\frac{ab+b}{d}$，由 $\phi \left(m\right)=\frac{ab+b}{d}\phi \left(d\right)\le \left|ab\right|+\left|b\right|$，得 $\phi \left(m\right)\in \left[1,\left|ab\right|+\left|b\right|\right]$，由推论2.7得 $m\in \left[1,{\left(\left|ab\right|+\left|b\right|\right)}^{3/2}+8\right]$。同理可得 $n\in \left[1,{\left(\left|ab\right|+\left|a\right|\right)}^{3/2}+8\right]$。

情形2 $c\ne 0$。此时方程(1)化为方程(3)，且由定理2.3知， $c_{1}d+ab\ne 0$。

当 $c_{1}d+ab>0$ 时。由方程(3)得 $d{m}_1-b=\frac{c_{1}d+ab}{d{n}_1-a}$。可知当 $d{n}_1-a=\text{1}$ 时， $m_1$ 取得最大值 $\frac{c_{1}d+ab+b}{d}$，故 $\phi \left(m\right)=m_1\phi \left(d\right)$ 取得最大值 $c+\frac{\phi \left(d\right)\left(ab+b\right)}{d}\le \left|c\right|+\left|ab\right|+\left|b\right|$，所以 $\phi \left(m\right)\in \left[1,\left(\left|c\right|+\left|ab\right|+\left|b\right|\right)\right]$，由推论2.7得 $m\in \left[1,{\left(\left|c\right|+\left|ab\right|+\left|b\right|\right)}^{3/2}+8\right]$。同理可得 $n\in \left[1,{\left(\left|c\right|+\left|ab\right|+\left|a\right|\right)}^{3/2}+8\right]$。

$c_{1}d+ab<0$ ( $c\le 0,c+ab<0$ 时，方程(1)有有限个解)，当 $d{n}_1-a=-1$ 时， $m_1=\frac{-c_{1}d-ab+b}{d}$，故 $\phi \left(m\right)=m_1\phi \left(d\right)=-c-\frac{\phi \left(d\right)\left(ab-b\right)}{d}\le \left|c\right|+\left|ab\right|+\left|b\right|$，所以 $\phi \left(m\right)\in \left[1,\left|c\right|+\left|ab\right|+\left|b\right|\right]$，由推论2.7得 $m\in \left[1,{\left(\left|c\right|+\left|ab\right|+\left|b\right|\right)}^{3/2}+8\right]$。同理可得 $n\in \left[1,{\left(\left|c\right|+\left|ab\right|+\left|a\right|\right)}^{3/2}+8\right]$。证毕。

注释：由定理3.4的证明过程我们可得以下特殊情形(表1)：

1.为了简化证明过程和统一结果，定理3.4中给出的解的范围有些偏大，对于具体给定的系数 $\left(a,b,c\right)$，该范围可适当缩小。如 $\left(a,b,c\right)=\left(-2,-6,20\right)$ 时，具体讨论后解的范围为 $m\in \left[1,\text{140}\right],n\in \left[1,\text{172}\right]$ (实际上，其全部解 $\left(3,4\right),\left(4,3\right)$ )，而定理中给出的解的范围是 $m\in \left[1,\text{242}\right],n\in \left[1,\text{206}\right]$。

2.以下情况方程(1)的解数有限(不包括无解)：

1) $c=0,ab\ne 0$ ；

2) $c\ge 0,c+ab>0$，特别当 $c=0,a=b>0$ 时，易知此时 $\left(\text{2}a,2a\right)$ 为方程(1)的一个解；

3) 当 $c\le 0,c+ab<0$。

3.以下情况方程(1)无正整数解

1) $c\le 0,a\le 0,b\le 0$ ；

2) $a,b$ 都为偶数，c为奇数；

3) $\left(a,b,c\right)$ 为本原勾股数，即 $\gcd \left(a,b\right)=1$，且满足 $a^2+b^2=c^2$。

Table 1. Some examples

表1. 一些算例

注1：全部解为： $\left\{\left(m,n\right)|m=7,9,14,18,\gcd \left(m,n\right)=1\right\}$，或 $\left\{\left(m,n\right)|m=12,\gcd \left(m,n\right)=3\right\}$，或 $\left\{\left(m,n\right)|m=6,\gcd \left(m,n\right)=6\right\}$ ；

注2：全部解为： $\left\{\left(m,n\right)|n=5,10,gcd\left(m,n\right)=5\right\}$ ；

注3：全部解为： $\left\{\left(m,n\right)|m=7,9,14,18,\gcd \left(m,n\right)=1\right\}$， $\left\{\left(4,22\right),\left(6,22\right),\left(20,2\right),\left(24,2\right),\left(30,2\right),\left(38,4\right),\left(38,6\right),\left(54,4\right)\right\}$ ；

注4：方程 $\phi \left(mn\right)=4\phi \left(m\right)+7\phi \left(n\right)+8$ 的所有整数解为：

$\begin{array}{l}\left(x,y\right)=\left(15,41\right),\left(16,41\right),\left(20,41\right),\left(24,41\right),\left(30,41\right),\left(16,55\right),\left(24,55\right),\left(16，75\right),\left(15,82\right),\left(15,88\right),\\ \left(11,17\right),\left(11,32\right),\left(11,34\right),\left(11,40\right),\left(11,48\right),\left(11,60\right),\left(22,17\right),\left(17,15\right),\left(17,16\right),\left(17,20\right),\\ \left(17,24\right),\left(17,30\right),\left(32,15\right)\left(34,15\right),\left(8,70\right),\left(8,78\right),\left(8,90\right),\left(10,52\right),\left(10,56\right),\left(10,72\right),\\ \left(10,78\right),\left(10,84\right),\left(12,70\right),\left(9,48\right),\left(9,60\right),\left(15,24\right),\left(24,15\right),\left(27,12\right),\left(8,52\right),\left(8,84\right),\\ \left(12,52\right),\left(12,56\right),\left(8,56\right),\left(8,72\right),\left(10,20\right),\left(10,30\right).\end{array}$

注5：方程 $\phi \left(mn\right)=3\phi \left(m\right)+5\phi \left(n\right)-13$ 的所有整数解为：

$\left(x,y\right)=\left(16,2\right),\left(20,2\right),\left(24,2\right),\left(30,2\right).$

注6：方程 $\phi \left(mn\right)=5\phi \left(m\right)+6\phi \left(n\right)+16$ 的所有整数解为：

$\begin{array}{l}\left(x,y\right)=\left(8,38\right),\left(8,54\right)，\left(10,38\right),\left(10,54\right),\left(12,38\right),\left(15,29\right),\left(15,58\right),\left(16,29\right),\left(20,10\right),\left(20,29\right),\\ \left(24,29\right),\left(30,10\right),\left(30,29\right),\left(48,138\right),\left(53,7\right),\left(53,9\right),\left(53,14\right),\left(53,18\right),\left(60,138\right),\left(75，12\right).\end{array}$

注7：方程 $\phi \left(mn\right)=11\phi \left(m\right)+11\phi \left(n\right)$ 的全部整数解是：

$\begin{array}{l}\left(x,y\right)=\left(13,161\right),\left(13,201\right),\left(13,207\right),\left(13,268\right),\left(13,322\right),\left(13,402\right),\left(13,414\right),\left(21,268\right),\left(26,161\right),\\ \left(26,201\right),\left(26,207\right),\left(36,161\right),\left(161,13\right),\left(201,13\right),\left(207,13\right),\left(268,13\right),\left(322,13\right),\left(402,13\right),\\ \left(414,13\right),\left(268,21\right),\left(161,26\right),\left(201,26\right),\left(207,26\right),\left(161,36\right),\left(22,22\right),\left(33,44\right),\left(44,33\right).\end{array}$

注8：方程 $\phi \left(mn\right)=\text{7}\phi \left(m\right)+\text{7}\phi \left(n\right)$ 的所有整数解为：

$\begin{array}{l}\left(x,y\right)=\left(87,16\right),\left(87,20\right),\left(116,15\right),\left(16,87\right),\left(20,87\right),\left(15,116\right),\left(8,58\right),\left(10,58\right),\\ \left(12,58\right),\left(58,8\right),\left(58,10\right),\left(58,12\right),\left(21,28\right),\left(28,21\right),\left(14,14\right).\end{array}$

注9：方程 $\phi \left(mn\right)=4\phi \left(m\right)+4\phi \left(n\right)$ 的所有整数解为：

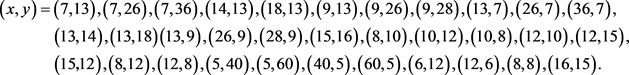
注10：方程 $\phi \left(mn\right)=7\phi \left(m\right)+9\phi \left(n\right)$ 的所有整数解为：

$\begin{array}{l}\left(x,y\right)=\left(73,15\right),\left(73,16\right),\left(73,20\right),\left(73,24\right),\left(73,30\right),\left(91,15\right),\left(91,16\right),\left(91,20\right),\left(91,24\right),\left(91,30\right),\\ \left(95,16\right),\left(95,24\right),\left(111,16\right),\left(111,20\right),\left(117,16\right),\left(117,20\right),\left(135,16\right),\left(135,20\right),\left(146,15\right),\\ \left(148,15\right),\left(152,15\right),\left(182,15\right),\left(31,11\right),\left(31,22\right),\left(31,11\right),\left(62,11\right),\left(17,32\right),\left(17,40\right),\\ \left(17,48\right),\left(17,60\right),\left(32,17\right),\left(40,17\right),\left(48,17\right),\left(60,17\right),\left(13,29\right),\left(13,58\right),\left(21,29\right),\left(21,58\right),\\ \left(26,29\right),\left(28,29\right),\left(36,29\right),\left(42,29\right),\left(11,71\right),\left(11,142\right),\left(22,71\right),\left(74,8\right),\left(74,10\right),\left(74,12\right),\\ \left(76,10\right),\left(114,8\right),\left(114,10\right),\left(126,8\right),\left(126,10\right),\left(16,30\right),\left(30,16\right),\left(76,8\right),\left(108,8\right),\left(76,12\right),\\ \left(16,20\right),\left(20,16\right),\left(20,24\right),\left(24,20\right),\left(35,15\right),\left(35,20\right),\left(35,30\right),\left(45,20\right),\left(70,15\right),\left(16,16\right).\end{array}$