一种带分布式自适应时延的粒子群算法

A Particle Swarm Optimization Algorithm with Distributed Adaptively Weighted Delays

摘要: 针对粒子群算法(PSO)容易陷入局部最优值、收敛精度低等缺陷，提出一种新的带分布式自适应时延的粒子群算法(PSO-DW)。改进的算法主要在RODDPSO算法的基础上考虑时延的时变性和种群的进化状态，以平衡算法的全局搜索和局部搜索能力，降低早熟收敛的可能性，提高算法的收敛速度和精度。主要思想：1) 在引入了分布式时延的速度更新公式中，每个时延项配以自适应权重，2) 引入通过当前状态和概率转移矩阵预测下一进化状态的预测机制，3) 分布式时延的强度因子由预测状态所确定。在九个基准函数上与四个算法作对比的实验结果表明，改进后的算法在寻优质量、稳定性、收敛速度等方面更具优越性。

Abstract: A new particle swarm optimization algorithm (PSO) with distributed adaptively weighted delays (PSO-DW) has been proposed to overcome the defects of the PSO algorithm, such as falling into local optimal value, low convergence accuracy. Based on the RODDPSO algorithm, the improved algorithm further considers the time-varying delays and the evolutionary states of the population, so that it can balance the global search and local search ability of the algorithm, reduce the possibility of premature convergence, and improve the convergence speed and accuracy of the algorithm. The main ideas are: 1) each delay is equipped with adaptive weight in the velocity update formula; 2) prediction mechanism of the next evolutionary state has been introduced by the current state and probability transfer matrix; 3) intensity factor of the distributed delay is determined by the prediction state. The experimental results show that the improved algorithm has more advantages in optimizing quality, stability and convergence speed by comparing with four algorithms on nine benchmark functions.

1. 引言

粒子群算法(particle swarm optimization, PSO)是一种基于群体智能的随机全局优化算法 [1]，最初由Eberhart和Kennedy (1995) [2] 受鸟群捕食行为启发而提出，其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。由于算法简单、易于实现、快速收敛等特性，PSO算法自从提出之日起就受到很多学者的青睐。近些年来PSO算法得到长足的发展并被广泛应用到实际领域的优化问题中。但粒子群算法依旧存在容易陷入局部最优从而导致早熟收敛的缺陷，这种缺陷随搜索空间维数的增大愈发明显。为了增加粒子的多样性以减少陷入局部收敛的可能性，学者们提出了各种改进策略来提高PSO算法的优化性能。基于参数调整的PSO算法有PSO-LDIW (Shi, 1998, 1999) [3] [4] [5]、PSO-CK (Clerc和Kennedy, 2002) [6]、PSO-TVAC (Ratnaweera, 2004) [7]、NCPSO (2017) [8]、AWPSO (Liu and Wang, 2019) [9] 等。基于拓扑结构和学习策略的改进算法有APSO (Zhan等人，2009) [10]、SPSO (Tang等人，2011) [11]、SDPSO (Zeng等人，2016) [12]、MDPSO (Song等人，2017, 2018) [13] [14] 等。这些算法通过考虑粒子群的四种进化状态和时延影响等因素大大提高了PSO算法的性能。2019年，Liu等人 [9] 提出了一种基于随机分布式时延的PSO算法(RODDPSO)，大大提高了算法的搜索能力，但是这种算法忽略了不同阶段的历史信息对当前状态的影响是不同的。事实上，离当前状态越近的历史信息对当前状态的影响较大，而越远的历史信息对当前状态的影响相对较小。

本文拟在RODDPSO算法的基础上，充分考虑不同历史信息对当前状态的影响，提出一种带分布式自适应时延的粒子群算法(PSO-DW)。改进算法中时延是具有时变性的，分布式时延的强度因子由预测状态所确定。新算法能进一步平衡全局搜索能力和局部搜索能力，降低早熟收敛的可能，提高算法的收敛速度和精度。仿真实验在150维搜索空间的九个基准函数上与四个算法作对比。结果表明，改进后的算法在寻优质量、稳定性、收敛速度等方面更具优越性。

2. 传统PSO算法

在PSO算法中，所有的粒子构成种群，并且每一个粒子都可能是所研究优化问题的最优解。粒子在搜索空间中根据个体的最优位置和群体最优位置更新速度和位置，从而寻找最优解 [15]。设种群由S个粒子组成，记集合 $I=\left\{1,2,3,\cdots ,S\right\}$。设搜索空间为 $R^D$，其中D为维数。用 $X_i\in R^D,i\in I$ 表示第i个粒子的位置，其速度为 $V_i\in R^D$。第i个粒子第k次迭代后的速度和位置分别是：

$V_i^{\left(k\right)}=\left(V_{i1}^{\left(k\right)},V_{i2}^{\left(k\right)},\cdots ,V_{iD}^{\left(k\right)}\right),$

$X_i^{\left(k\right)}=\left(X_{i1}^{\left(k\right)},X_{i2}^{\left(k\right)},\cdots ,X_{iD}^{\left(k\right)}\right).$

令 $P_i=\left(P_{i1},P_{i2},\cdots ,P_{iD}\right)$ 表示第i个粒子的最优位置， $P_G=\left(P_{G1},P_{G2},\cdots ,P_{GD}\right)$ 表示种群全局最优位置 [16]。在搜索的过程中，所有的粒子都朝着全局最优的方向移动。第i个粒子在k + 1时刻的速度和位置的更新公式为：

$\begin{array}{l}{V}_i^{\left(k+1\right)}=\omega V_i^{\left(k\right)}+c_1{r}_1\left(P_i^{\left(k\right)}-X_i^{\left(k\right)}\right)+c_2{r}_2\left(P_G^{\left(k\right)}-X_i^{\left(k\right)}\right),\\ X_i^{\left(k+1\right)}=X_i^{\left(k\right)}+V_i^{\left(k+1\right)}.\end{array}$ (1)

在公式(1)中， $\omega$ 是惯性权重； $r_1,r_2$ 都是D维向量，其每个分量都是 $\left[0,1\right]$ 上的随机数； $c_1,c_2$ 分别表示个体认知加速度系数和社会认知加速度系数。

为了提高搜索速度，Clerc和Kennedy (2002)提出了PSO-CK算法 [6]；在此算法中通过大量的实验证明当 $c_1=c_2=1.49,\omega =0.729$ 时性能最优。为了平衡当前速度、认知和社会等方面的性能，Shi和Eberhart博士先后在1998年和1999年提出了PSO-LDIW算法 [3] [4] [5]，该算法采用了线性下降的惯性权重：

$\omega ={\omega }_{\max }-\left({\omega }_{\max }-{\omega }_{\min }\right)\times \frac{iter}{maxiter},$ (2)

这里 ${\omega }_{\max }$ ( ${\omega }_{\min }$ )为在整个搜索过程中惯性权重的最大(最小)的值； $iter$ ( $maxiter$ )表示当前(最大)的迭代次数。受时变惯性权重的启发，Ratnaweera等人在2004年提出了PSO-TVAC算法 [7]，将加速度因子改进为：

$c_1=\left(c_{1i}-c_{1f}\right)\times \frac{maxiter-iter}{maxiter}+c_{1f}$ (3)

$c_2=\left(c_{2i}-c_{2f}\right)\times \frac{maxiter-iter}{maxiter}+c_{2f}$ (4)

上式中 $c_{1i}$ ( $c_{1f}$ )和 $c_{2i}$ ( $c_{2f}$ )分别是个体认知加速度系数和社会认知加速度系数的初值(终值)，这些参数的取值为：

$c_{1i}=2.5,c_{1f}=0.5,c_{2i}=0.5,c_{2f}=\mathrm{2.5.}$

3. 改进的粒子群算法

本文提出一个带有分布式自适应时延和与由预测状态所确定的强度因子的粒子群优化(PSO-DW)算法。

3.1. 进化状态的刻画与预测

进化状态这一概念先后由Zhan [10]、Tang [11] 等人根据种群分布信息提出。整个搜索过程包含四种状态：收敛、开发、勘探和跳出，分别用 $\xi =1,2,3,4$ 表示。记

$d_i=\frac{1}{S-1}{\displaystyle \underset{j=1,i\ne j}{\overset{S}{\sum }}\sqrt{{\displaystyle \underset{l=1}{\overset{D}{\sum }}{\left(x_{il}-x_{jl}\right)}^2}}},i\in I$ (5)

表示第i个粒子和其余粒子间的平均距离， $d_{\min },d_{\max }$ 是集合 $\left\{d_i|i\in I\right\}$ 中的最小值和最大值，用G表示全局最优粒子。定义

$E_f=\frac{d_G-d_{\min }}{d_{\max }-d_{\min }},$ (6)

显然 $E_f\in \left[0,1\right]$ 且在收敛状态下粒子群将紧跟当前全局最优粒子飞向最优解，此时 $E_f$ 会逐渐减小；而在跳出状态下全局最优粒子倾向于远离种群，此时 $E_f$ 相对较大。因此 $E_f$ 能恰当刻画种群的进化状态，称 $E_f$ 为进化因子。根据 $E_f$ 的取值，规定：

$\xi =\{\begin{array}{l}1,0.00\le E_f<0.25,\\ 2,0.25\le E_f<0.50,\\ 3,0.50\le E_f<0.75,\\ 4,0.75\le E_f\le 1.\end{array}$ (7)

在种群进化过程中，下一进化状态不可避免的受到当前状态的影响，本文引入一种预测机制，利用概率转移矩阵来通过当前进化状态对下一状态进行预测。记 ${\xi }^{\left(k\right)}$ 为第k次迭代时的当前进化状态， ${{\xi }^{\prime }}^{\left(k\right)}$ 为预计的下一进化状态。取概率转移矩阵为：

$M^{\left(k\right)}=\left[\begin{array}{cccc}\phi & 1-\phi & 0& 0\\ \frac{1-\phi }{2}& \phi & \frac{1-\phi }{2}& 0\\ 0& \frac{1-\phi }{2}& \phi & \frac{1-\phi }{2}\\ 0& 0& 1-\phi & \phi \end{array}\right]$ (8)

其中

$M_{ij}^{\left(k\right)}=P\left\{{{\xi }^{\prime }}^{\left(k\right)}=j|{\xi }^{\left(k\right)}=i\right\},\forall i,j=1,2,3,4$

表示种群根据当前进化状态i去预测下一状态j的概率，满足 ${\displaystyle {\sum }_{j=1}^4{M}_{ij}^{\left(4\right)}}=1$。这里 $\phi$ 是一个非常重要的参数。为既保持种群进化的惯性，也增加其多样性，本文参考Zeng [12]，选取 $\phi =0.9$。这意味着种群有很大的可能维持当前的状态，而以较小的概率转移到另一进化状态。

3.2. 新算法的构建

传统的粒子群算法专注于当前信息对寻找最优解的影响而忽略了过去的信息。但在实际搜索过程中每一个粒子对每次迭代的速度、位置、个体最优以及全局最优等信息都保留有记忆，充分综合这些信息更有利于种群搜索最优解。2019年Liu等人引入随机分布式时延项，提出RODDPSO算法 [9]，此算法不仅考虑种群当前状态的个体最优和全局最优信息，还充分考虑历史上个体最优和全局最优信息，但是忽略了不同阶段的历史信息对当前状态的影响是不同。事实上，离当前状态越近的历史信息对当前状态的影响较大，而越远的历史信息对当前状态的影响相对较小。基于这一事实，本文提出一种带有分布式自适应时延的粒子群算法(PSO-DW)，其更新公式为：

$\begin{array}{l}{V}_i^{\left(k+1\right)}=\omega V_i^{\left(k\right)}+c_1{r}_1\left(P_i^{\left(k\right)}-X_i^{\left(k\right)}\right)+c_2{r}_2\left(P_G^{\left(k\right)}-X_i^{\left(k\right)}\right)\\ +m_l\left({{\xi }^{\prime }}^{\left(k\right)}\right)c_3{r}_3{\displaystyle \underset{\tau =1}{\overset{N}{\sum }}{\omega }_1}{\alpha }_{\left(\tau \right)}\left(P_i^{\left(k-\tau \right)}-X_i^{\left(k\right)}\right)\\ +m_G\left({{\xi }^{\prime }}^{\left(k\right)}\right)c_4{r}_4{\displaystyle \underset{\tau =1}{\overset{N}{\sum }}{\omega }_1}{\alpha }_{\left(\tau \right)}\left(P_G^{\left(k-\tau \right)}-X_i^{\left(k\right)}\right),\\ X_i^{\left(k+1\right)}=X_i^{\left(k\right)}+V_i^{\left(k+1\right)}.\end{array}$ (9)

对比式(1)，这里引进了关于个体认知和社会认知的分布式时延项。其中 $\tau$ 是时延的步数，可取值 $1,2,\cdots ,N$，N为分布式时延步数的上限值； ${\omega }_1$ 是当时延发生时的自适应权重，它决定了每个时延影响的大小； ${\alpha }_{\left(\tau \right)}$ 从 $\left\{0,1\right\}$ 中随机选取，以增加粒子的多样性； $c_3,c_4$ 是加速度系数； $r_3,r_4$ 是 $\left[0,1\right]$ 上服从均匀分布的随机向量； $m_l\left({{\xi }^{\prime }}^{\left(k\right)}\right)$ 和 $m_G\left({{\xi }^{\prime }}^{\left(k\right)}\right)$ 是分布式时延项的强度因子，由预测的进化状态 ${{\xi }^{\prime }}^{\left(k\right)}$ 确定，主要用来提高算法的搜索能力和加快收敛速度。需要说明的是当 $\tau \ge k$ 时约定 $P_i^{\left(k-\tau \right)}=P_i^{\left(k\right)}$， $P_G^{\left(k-\tau \right)}=P_G^{\left(k\right)}$。

3.3. 参数配置

新的粒子群算法带有两个权重参数 $\omega$ 和 ${\omega }_1$。其中惯性权重 $\omega$ 由式(2)确定；自适应权重 ${\omega }_1$ 用来控制时延项对速度的影响，它是时变的，为关于 $\tau$ 的递减函数，本文取

${\omega }_1=\frac{N-\tau }{N},$ (10)

加速度系数 $c_1,c_2$ 由式(3)、(4)确定， $c_3,c_4$ 与 $c_1,c_2$ 所起作用类似，本文取 $c_3=c_1$， $c_4=c_2$。强度因子 $m_l\left({{\xi }^{\prime }}^{\left(k\right)}\right)$ 和 $m_G\left({{\xi }^{\prime }}^{\left(k\right)}\right)$ 主要用来提高算法的搜索能力，加快算法的收敛速度，初值都取为0，在进化过程中，其大小由预测状态所确定(见表1)。当根据k次迭代后种群的状态预测到下一状态是收敛状态时，粒子将紧跟全局最优粒子快速到达最优解，为保持这种趋势，忽略时延项的影响而取 $m_l\left(1\right)=m_G\left(1\right)=0$ ；当预测到下一状态是开发状态时，粒子将在个体最优位置仔细搜索，因此个体的历史最优位置有着重要的参考意义，取 $m_l\left(2\right)=0.01$， $m_G\left(2\right)=0$。当预测到下一状态是勘探状态时，粒子将在整个搜索空间尽可能的探索全局最优解，此时需充分考虑全局历史最优信息，取 $m_l\left(3\right)=0$， $m_G\left(3\right)=0.01$ ；当预测到下一状态是跳出状态时，个体和全局的历史最优位置需要综合考虑，取 $m_l\left(4\right)=0.01$， $m_G\left(4\right)=0.01$。需指出的是参数0.01是个经验值。

Table 1. Intensity factor selection strategy

表1. 强度因子选择策略

4. 仿真实验与结果分析

4.1. 实验环境

为验证新算法的性能，本文引入九个基准函数进行测试，其中既有单峰函数又有多峰函数，基准函数的具体信息见表2；本文实验在高维搜索空间进行，取维数 $D=150$，粒子数 $S=20$，最大迭代次数为20,000次，为消除随机因素的影响，每次实验重复40次，最后取平均值。每次实验之初随机初始化粒子的速度 $V_i$ 和位置 $X_i,i\in I$，然后计算出每一个粒子的适应度值，根据适应度值确定个体最优粒子的位置 $P_i$ 和全局最优粒子的位置 $P_G$。

4.2. 上限值N的选取

在PSO-DW算法中，分布式时延步数的上限值N是一个非常重要的参数，不同的N将影响算法的收敛速度和最终的收敛值。本文将通过实验，对比N取75、100、125、150、175、200时，根据算法在150维空间中的九个基准函数上的不同表现，选取鲁棒性最强的N。实验结果如图1所示。在图1中，纵坐标是平均适应度值的对数值，横坐标是迭代次数。

从图1中可以看出，当分布时延项数的上限值N取125时算法在 $f_1\left(x\right)$， $f_3\left(x\right)$， $f_8\left(x\right)$， $f_9\left(x\right)$ 相对于其他的N性能更优，不仅拥有较好的适应度值,而且相对而言较早开始收敛。对于函数 $f_2\left(x\right)$， $f_4\left(x\right)$， $f_5\left(x\right)$， $f_6\left(x\right)$， $f_7\left(x\right)$，虽然N取125没有最优的适应度值，但与其它适应度值相差不大，而 $N=125$ 时有更早的收敛趋势，因此本文选取 $N=125$。

Table 2. Benchmark function

表2. 基准函数

$f_1\left(x\right)$ $f_2\left(x\right)$ $f_3(\; x\; )$

$f_4\left(x\right)$ $f_5\left(x\right)$ $f_6(\; x\; )$

$f_7\left(x\right)$ $f_8\left(x\right)$ $f_9(\; x\; )$

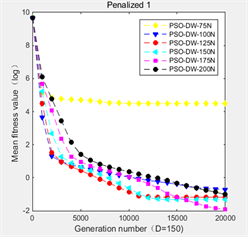
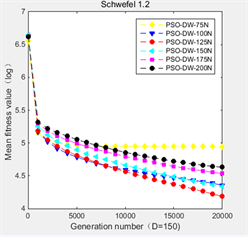
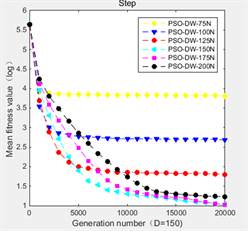
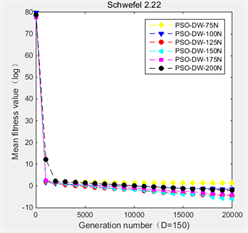
Figure 1. Training N by PSO-DW algorithm

图1. 由PSO-DW算法训练N

4.3. 实验结果与分析

为验证算法性能在高维搜索空间中的优越性，本文选用PSO-CK、PSO-TVAC、PSO-LDIW、RODDPSO四种算法作对比，评价指标为最小值、均值、方差。实验结果如表3和图2所示。表3表明，在相同的实验环境下，PSO-DW算法在九个基准函数上表现出明显优势。首先九个平均适应度值都是最小的，这表明PSO-DW算法有较好的寻优质量，其收敛精度更高；其次除了在 $f_4\left(x\right)$ 上，PSO-DW算法的方差也是最小的，这说明PSO-DW算法的稳定性较好；就最小值而言PSO-DW算法的仅在 $f_3\left(x\right)$ 上略逊于PSO-CK算法。进一步仔细比较，算法性能表现次优的是RODDPSO算法，而PSO-CK、PSO-TVAC、PSO-LDIW算法精确度普遍较差，这表明在高维搜索空间中，PSO-CK、PSO-TVAC、PSO-LDIW算法容易收敛于局部极值，而引入时延项的PSO算法，充分考虑了种群的个体最优历史信息和全局历史信息，更加有利于增加粒子的多样性，表现出更好的跳出局部最优的能力。

Table 3. Comparison of performance of five algorithms in 150 D search space

表3. 五种算法在150D的搜索空间中的性能比较

图2表明在150维搜索空间中，五种算法都有较好的收敛，但PSO-DW的优势更加明显。由于分布式时延的引入，历史最优信息被充分考虑，PSO-DW和RODDPSO算法在寻优前期都表现出较好的全局搜索能力，快速朝最优解方向搜索，并且在寻优中期和晚期中表现出较好的局部搜索和跳出局部最优的能力，实现收敛能力的提升。对比RODDPSO算法，一方面由于考虑了时延的时变性，PSO-DW算法具有更加准确的搜索性能，大大提升了收敛精确度；另一方面，由预计状态确定的强度因子的引入，促使种群由当前状态快速向下一进化状态转化，加快了算法的收敛速度。综上所述，在150维的搜索空间中，改进的PSO-DW算法在搜索过程中较好地平衡了全局搜索和局部搜索的能力，降低了陷入局部最优的可能性，实现了收敛速度和收敛精度的提升。

$f_1\left(x\right)$ $f_2\left(x\right)$ $f_3(\; x\; )$

$f_4\left(x\right)$ $f_5\left(x\right)$ $f_6(\; x\; )$

$f_7\left(x\right)$ $f_8\left(x\right)$ $f_9(\; x\; )$

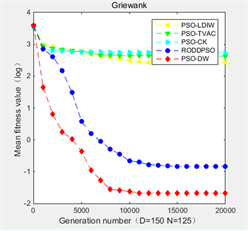
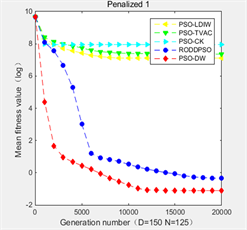
Figure 2. Comparison of five algorithms in 150-dimensional search space

图2. 五种算法在150维的搜索空间中的对比图

5. 结论

考虑到种群的进化状态和历史最优信息，本文提出一种带分布式自适应时延的粒子群优化算法(PSO-DW)，该算法大大降低了种群在搜索过程中陷入局部最优的可能性，提升了收敛速度和收敛精度。实验在150维搜索空间进行，迭代20,000次，每次实验重复40次，工作量较大；实验结果表明在高维搜索空间中新算法有较好的寻优能力和稳定性。

基金项目

本项目由国家自然科学基金项目：61873169资助。