非奇异H-矩阵的一组细分迭代实用判定方法

A Set of Subdivision Iteration Practical Criteria for Nonsingular H-Matrix

摘要: 非奇异H-矩阵广泛应用于计算数学、控制理论、弹性力学以及神经网络系统等研究领域，但对非奇异H-矩阵的判定十分困难。本文研究了非奇异H-矩阵判定条件，通过对矩阵指标集按要求细分和构造递进的正对角矩阵元素，得到了非奇异H-矩阵的一组细分迭代实用判定方法，并给出证明，运用数值算例表明新判定条件优于已知结果。

Abstract: Nonsingular H-matrices have been widely used in many fields, such as computational mathematics, control theory, elastic mechanics, neural network system, etc. But it is very difficult to judge nonsingular H-matrix. In this paper, the criteria for nonsingular H-matrices are studied. By subdividing the matrix index set according to the requirements and constructing progressive diagonal matrix elements, a set of new subdividing iterative criteria for nonsingular H-matrices are obtained and proved. Finally, numerical examples show that the new decision condition is superior to the known results.

1. 引言

非奇异H-矩阵作为特殊矩阵中的重要矩阵类，其数值判定方法一直是研究的热点问题，国内外学者从不同的角度进行了研究，给出了许多研究成果 [1] - [12]。其中，文献 [1] 利用不等式放缩技巧，改进放缩因子，得到一组一般的判定条件。文献 [2] 将判定不等式的放缩因子迭代，给出判定非奇异H-矩阵的迭代式新条件，文献 [3] 根据行和与对角元素的关系将非对角占优的集合进行m-级划分，从而得到判定非奇异H-矩阵更为高效的方法。文献 [4] 提出将细分指标集和迭代放缩因子结合，得到了非奇异H-矩阵的细分迭代判别条件。本文在上述基础上，对非对角占优行指标集m-级划分的同时，改进了判定条件中的递进迭代系数，构造新的正对角矩阵，推广和改进了已知的相关结果，并通过若干个数值算例对比分析，说明了新判定方法的优越性。

首先记 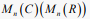为 $n$ 阶复(实)矩阵的集合， $N=1,2,\cdots ,n$，设 $A=\left(a_{ij}\right)\in M_n\left(C\right)$，又记 ${\Lambda }_i\left(A\right)={\displaystyle \underset{j\ne i}{\sum }\left|a_{ij}\right|}$，文中简记 ${\Lambda }_i\left(A\right)={\Lambda }_i$。对 $\forall i\in N$，如果 $\left|a_{ii}\right|\ge {\Lambda }_i\left(A\right)$，则称A为对角占优矩阵；对 $\forall i\in N$，如果 $\left|a_{ii}\right|>{\Lambda }_i\left(A\right)$，则称A为严格对角占优矩阵，记为 $A\in D$ ；若存在正对角阵X，使得 $AX$ 为严格对角占优矩阵，则称A为非奇异H-矩阵，记为 $A\in \tilde{D}$。

定义1 [5] 设 $A=\left(a_{ij}\right)\in M_n\left(C\right)$ 为不可约矩阵，若 $\left|a_{ii}\right|\ge {\Lambda }_i\left(A\right)\left(i\in N\right)$，且其中至少有一个严格不等式成立，则A为不可约对角占优矩阵。

定义2 [6] 设 $A=\left(a_{ij}\right)\in M_n\left(C\right)$，若对满足 $\left|a_{ii}\right|\ge {\Lambda }_i\left(A\right)\left(i\in N\right)$，且其中至少有一个严格不等式成立，又对每个等式的下标i，都存在非零元素链 $a_{i{j}_1}{a}_{j_1{j}_2}\cdots a_{j_{k-1}{j}_k}\ne 0$，使得 $\left|a_{j_k{j}_k}\right|>{\Lambda }_{j_k}\left(A\right)$，则称A为具非零元素链对角占优矩阵。

引理1 [7] 设 $A=\left(a_{ij}\right)\in M_n\left(C\right)$ 为不可约对角占优矩阵，则 $A\in \tilde{D}$。

引理2 [7] 设 $A=\left(a_{ij}\right)\in M_n\left(C\right)$ 为具有非零元素链对角占优矩阵，则 $A\in \tilde{D}$。

记，

$\begin{array}{l}{N}_1=\left\{i\in N:0<\left|a_{ii}\right|<{\Lambda }_i\right\},N_2=\left\{i\in N:\left|a_{ii}\right|={\Lambda }_i\right\},\\ N_3=\left\{i\in N:\left|a_{ii}\right|>{\Lambda }_i\left(A\right)\right\},N=N_1\oplus N_2\oplus N_3.\end{array}$

显然，如果 $N_3$ 为空集，那么 $A\notin \tilde{D}$ ；如果 $N_1\cup N_2=\varnothing$，则 $A\in D$。因而我们假设集合 $N_1\cup N_2$ 是非空的，集合 $N_3$ 也是非空的。因为非奇异H-矩阵的主对角线上的元素都是非零的，所以本文中涉及的矩阵对角元均假设为非零。另外，在本文中总假定矩阵每行中的非主对角线上的元素模和为正。

将 $N_1$ 进一步划分 $N_1=N_{{}_1}^{(1)}\cup N_{{}_1}^{(2)}\cup \cdots \cup N_{{}_1}^{(m)}$，其中m是任意正整数，取 $k\in Z^{+}$， $k\le m$，且

$N_{{}_1}^{(1)}=\left\{i\in N:0<\left|a_{ii}\right|<\frac{1}{m}{\Lambda }_i\left(A\right)\right\}$,

$N_{{}_1}^{(k)}=\left\{i\in N:\frac{k-1}{m}{\Lambda }_i\left(A\right)<\left|a_{ii}\right|<\frac{k}{m}{\Lambda }_i\left(A\right)\right\}$,

这里部分可能为空集。

2. 主要结果

为了叙述方便，引入以下符号：

$x_{1i}^{\left(k\right)}=\frac{\frac{k}{m}\left({\Lambda }_i-\frac{k}{k+1}\left|a_{ii}\right|\right)}{{\Lambda }_i}\left(i\in N_1^{\left(k\right)},k=1,2,\cdots ,m\right)$,

${\delta }_{0,i}=\frac{{\Lambda }_i\left(A\right)}{\left|a_{ii}\right|}\left(\forall i\in N_3\right)$, ${\delta }_{l,i}=\frac{P_{l,i}}{\left|a_{ii}\right|}\left(\forall i\in N_3,l\in Z^{\text{+}}\right)$,

$P_{l,i}\left(A\right)={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}{\delta }_{l-1,t}\left(\forall i\in N_3,l\in Z^{\text{+}}\right)$,

$x_{2i}=\frac{{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|}+}{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|{\delta }_{l,t}}}{\left|a_{ii}\right|}\left(\forall i\in N_2,l\in Z^{+}\right)$,

$Q_l=\underset{i\in N_3}{\max }\left(\frac{{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l,t}}}{P_{l,i}\left(A\right)}\right)\left(l\in Z^{+}\right)$.

规定：在本文定理中，对 $\forall i\in N_3$， $l\in Z^{+}$， ${\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)=0}$ 和 ${\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}{\delta }_{l-1,i}=0$ 不会同时存在。

2.1. 定理1

设 $A\in M_n\left(C\right)$，若存在 $l\in Z^{+}$，使得

$\left|a_{ii}\right|x_{1i}^{(k)}>{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)},t\ne i}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_1^{(k)},k=1,2,\cdots ,m\right)$, (1)

$\left|a_{ii}\right|x_{2i}>{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|}{x}_{2t}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_2\right)$, (2)

则 $A\in \tilde{D}$。

证明

根据 $x_{1i}^{\left(k\right)}$ 的定义可知，

$0<x_{1i}^{\left(k\right)}<1\left(\forall i\in N_1^{\left(k\right)},k=1,2,\cdots ,m\right)$,

又根据 $P_{l,i}\left(A\right)$ 的定义，对 $\forall i\in N_3$ 有

$P_{1,i}\left(A\right)={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}{\delta }_{0,t}<{\Lambda }_i\left(A\right)$,

即

${\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}\frac{P_{1,t}}{\left|a_{tt}\right|}<{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}\frac{{\Lambda }_t(A)}{\left|a_{tt}\right|}$,

则 $P_{2,i}\left(A\right)<P_{1,i}\left(A\right)$。故对 $\forall i\in N_3$，有 $P_{2,i}\left(A\right)<P_{1,i}\left(A\right)<1$，假设当 $l=n-1$ 时， $P_{n,i}<P_{n-1,i}$，则当 $l=n$ 时，由

${\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}\frac{P_{n,t}}{\left|a_{tt}\right|}<{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}\frac{P_{n-1,t}}{\left|a_{tt}\right|}$,

可得 $P_{n+i,i}\left(A\right)<P_{n,i}\left(A\right)$，故由数学归纳法知， $P_{l,i}<P_{l-1,i}<\mathrm{...}<P_{2,i}\left(A\right)<P_{1,i}\left(A\right)<{\Lambda }_i\left(A\right)$。

因为 ${\delta }_{l,i}=\frac{P_{l,i}}{\left|a_{ii}\right|}\left(i\in N_3,l\in Z^{+}\right)$，因此对 $\forall i\in N_3$， $l\in Z^{\text{+}}$，有

$0<{\delta }_{l,i}<{\delta }_{l-1,i}<\cdots <{\delta }_{1,i}<\frac{{\Lambda }_i\left(A\right)}{\left|a_{ii}\right|}<1$.

进而由 $x_{2i}$ 的定义，对 $\forall i\in N_2$，有 $0<x_{2i}<1$。因此对 $\forall i\in N_3$， $l\in Z^{\text{+}}$，有

$\frac{{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l,t}}}{P_{l,i}\left(A\right)}\le \frac{{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l,t}}}{{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)}+{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l-1,t}}}\le 1$.

故由 $Q_l$ 的定义，对 $\forall i\in N_3$， $l\in Z^{\text{+}}$，有 $0<Q_l\le 1$。

利用(1)式和(2)式，存在 $l\in Z^{\text{+}}$，可适当地选择充分小的 $\epsilon >0$，使 $\epsilon$ 同时满足

$\left|a_{ii}\right|x_{1i}^{(k)}>{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)},t\ne i}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}\left(Q_l{\delta }_{l,t}+\epsilon \right)\left(\forall i\in N_{{}_1}^{(k)},k=1,2,\cdots ,m\right)$, (3)

$\left|a_{ii}\right|x_{2i}>{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|}{x}_{2t}+{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}\left(Q_l{\delta }_{l,t}+\epsilon \right)\left(\forall i\in N_2\right)$, (4)

构造正对角矩阵 $D=diag\left(d_1,d_2,\cdots ,d_n\right)$，记 $B=AD=\left(b_{ij}\right)$，其中

$d_i=\{\begin{array}{l}{x}_{1i}^{(k)},i\in N_1^{(k)}\hfill \\ x_{2i},i\in N_2\hfill \\ Q_l{\delta }_{l,i}+\epsilon ,i\in N_3\hfill \end{array}$

1) 对 $\forall i\in N_1^{(k)}\left(k=1,2,\cdots ,m\right)$，由(3)式得

$\begin{array}{c}{\Lambda }_i\left(B\right)={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)},t\ne i}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}}+{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|\left(Q_l{\delta }_{l,t}+\epsilon \right)}\\ <\left|a_{ii}\right|x_{1i}^{(k)}=\left|b_{ii}\right|；\end{array}$

2) 对 $\forall i\in N_2$，由(4)式得

$\begin{array}{c}{\Lambda }_i\left(B\right)={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|x_{2t}}+{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|\left(Q_l{\delta }_{l,t}+\epsilon \right)}\\ <\left|a_{ii}\right|x_{2i}=\left|b_{ii}\right|；\end{array}$

3) 对 $\forall i\in N_3$， $l\in Z^{+}$，有 ${\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}<\left|a_{ii}\right|$，由

$Q_l\ge \frac{{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l,t}}}{P_{l,i}\left(A\right)}$,

得

$\begin{array}{c}{Q}_l{P}_{l,i}\left(A\right)\ge {\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l,t}}}\\ \ge {\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}+Q_l{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l,t}}}\end{array}$ (5)

$\begin{array}{c}{\Lambda }_i\left(B\right)={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}}+{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|\left(Q_l{\delta }_{l,t}+\epsilon \right)}\\ ={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+Q_l{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l,t}+\epsilon {\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}}\\ \le Q_l{P}_{l,i}\left(A\right)+\epsilon {\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}\\ <Q_l{\delta }_{l,i}\left|a_{ii}\right|+\epsilon \left|a_{ii}\right|=\left|b_{ii}\right|\end{array}$

综上所述， $\left|b_{ii}\right|>{\Lambda }_i\left(B\right)\left(\forall i\in N\right)$，即 $B\in D$，所以矩阵 $A$ 是非奇异H-矩阵。证毕。

注1 由于 $0<\frac{\frac{k}{m}\left({\Lambda }_i\left(A\right)-\frac{k}{k+1}\left|a_{ii}\right|\right)}{{\Lambda }_i\left(A\right)}<1\left(\forall i\in N_1^{\left(k\right)},k=1,2,\cdots ,m\right)$， $0<x_{2i}<1\left(\forall i\in N_2\right)$，则本文定理1在迭代判定时要比文 [1] 定理1的判定范围更宽，后面的数值算例可以详细说明。

在定理1中取 $m=1$，则 $x_{1i}=\frac{{\Lambda }_i\left(A\right)-\frac{1}{2}\left|a_{ii}\right|}{{\Lambda }_i\left(A\right)}\left(\forall i\in N_1\right)$，即得推论1。

2.1.1. 推论1

设 $A\in M_n\left(C\right)$，若存在 $l\in Z^{+}$，使得

$\left|a_{ii}\right|\frac{{\Lambda }_i\left(A\right)-\frac{1}{2}\left|a_{ii}\right|}{{\Lambda }_i\left(A\right)}>{\displaystyle \underset{t\in N_1,t\ne i}{\sum }\left|a_{it}\right|}\frac{{\Lambda }_t\left(A\right)-\frac{1}{2}\left|a_{tt}\right|}{{\Lambda }_t\left(A\right)}+{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_1\right)$,

$\left|a_{ii}\right|x_{2i}>{\displaystyle \underset{t\in N_1}{\sum }\left|a_{it}\right|}\frac{{\Lambda }_t\left(A\right)-\frac{1}{2}\left|a_{tt}\right|}{{\Lambda }_t\left(A\right)}+{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_2\right)$,

则 $A\in \tilde{D}$。

注2 因为 $0<\frac{{\Lambda }_i\left(A\right)-\left|a_{ii}\right|}{{\Lambda }_i\left(A\right)}<\frac{{\Lambda }_i\left(A\right)-\frac{1}{2}\left|a_{ii}\right|}{{\Lambda }_i\left(A\right)}<1\left(\forall i\in N_1\right)$， $0<x_{2i}<1\left(\forall i\in N_2\right)$，对 $\forall i\in N_3$， $l\in Z^{+}$，有 $0<Q_l\le 1$， $0<{\delta }_{l,i}<\frac{{\Lambda }_i\left(A\right)}{\left|a_{ii}\right|}<1$，此时本文推论1的迭代因子比文 [2] 和文 [4] 中定理1的迭代因子小。所以本文推论1的判定条件比文 [2] 定理1和文 [4] 定理1的条件弱，判定的矩阵范围更广。故本文推论1推广了文 [2] 的定理1和文 [4] 的定理1，后面的数值算例可以说明。

在定理1中取 $m=2$，则

$N_{{}_1}^{(1)}=\left\{i\in N:0<\left|a_{ii}\right|<\frac{1}{2}{\Lambda }_i\left(A\right)\right\}$, $N_{{}_1}^{(2)}=\left\{i\in N:\frac{1}{2}{\Lambda }_i\left(A\right)<\left|a_{ii}\right|<{\Lambda }_i\left(A\right)\right\}$,

即得推论2。

2.1.2. 推论2

设 $A\in M_n\left(C\right)$，若存在 $l\in Z^{+}$，使得

$\begin{array}{c}\left|a_{ii}\right|\frac{\frac{1}{2}\left({\Lambda }_i-\frac{1}{2}\left|a_{ii}\right|\right)}{{\Lambda }_i}>{\displaystyle \underset{t\in N_1^{(1)},t\ne i}{\sum }\left|a_{it}\right|}\frac{\frac{1}{2}\left({\Lambda }_t\left(A\right)-\frac{1}{2}\left|a_{ii}\right|\right)}{{\Lambda }_t\left(A\right)}+{\displaystyle \underset{t\in N_1^{(2)}}{\sum }\left|a_{it}\right|}\frac{{\Lambda }_t\left(A\right)-\frac{2}{3}\left|a_{ii}\right|}{{\Lambda }_t\left(A\right)}\\ +{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_1^{(1)}\right)，\end{array}$

$\begin{array}{c}\left|a_{ii}\right|\frac{{\Lambda }_i\left(A\right)-\frac{2}{3}\left|a_{ii}\right|}{{\Lambda }_i\left(A\right)}>{\displaystyle \underset{t\in N_1^{(1)}}{\sum }\left|a_{it}\right|}\frac{\frac{1}{2}\left({\Lambda }_t\left(A\right)-\frac{1}{2}\left|a_{ii}\right|\right)}{{\Lambda }_t\left(A\right)}+{\displaystyle \underset{t\in N_1^{(2)},t\ne i}{\sum }\left|a_{it}\right|}\frac{{\Lambda }_t\left(A\right)-\frac{2}{3}\left|a_{ii}\right|}{{\Lambda }_t\left(A\right)}\\ +{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_1^{(2)}\right)，\end{array}$

$\begin{array}{c}\left|a_{ii}\right|x_{2i}>{\displaystyle \underset{t\in N_1^{(1)}}{\sum }\left|a_{it}\right|}\frac{\frac{1}{2}\left({\Lambda }_t\left(A\right)-\frac{1}{2}\left|a_{ii}\right|\right)}{{\Lambda }_t\left(A\right)}+{\displaystyle \underset{t\in N_1^{(2)}}{\sum }\left|a_{it}\right|}\frac{{\Lambda }_t\left(A\right)-\frac{2}{3}\left|a_{ii}\right|}{{\Lambda }_t\left(A\right)}\\ +{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_2\right)，\end{array}$

则 $A\in \tilde{D}$。

注3 因为 $0<\frac{{\Lambda }_i\left(A\right)-\left|a_{ii}\right|}{{\Lambda }_i\left(A\right)}<\frac{{\Lambda }_i\left(A\right)-\frac{2}{3}\left|a_{ii}\right|}{{\Lambda }_i\left(A\right)}\left(\forall i\in N_1^{(2)}\right)$， $0<x_{2i}<1\left(\forall i\in N_2\right)$，又对 $\forall i\in N_3$， $l\in Z^{+}$， $0<Q_l{\delta }_{l,i}\le 1$，并且随着每次迭代 $Q_l{\delta }_{l,i}$ 的取值会逐渐变小，所以本文推论2改进了文 [3] 定理1的判定条件，后面的数值算例可以说明。

2.2. 定理2

设 $A\in M_n\left(C\right)$， $A$ 不可约，若存在 $l\in Z^{+}$，使得

$\left|a_{ii}\right|x_{1i}^{(k)}\ge {\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)},t\ne i}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_{{}_1}^{(k)},k=1,2,\cdots ,m\right)$,(6)

$\left|a_{ii}\right|x_{2i}\ge {\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|{\delta }_{l,t}}\left(\forall i\in N_2\right)$, (7)

且上式中至少有一个严格不等式成立，则 $A\in \tilde{D}$。

证明

因为A是不可约的，所以存在任一非空集， $K\subset N$， $\forall i\in K$， $j\in N/K$，有 $\left|a_{ij}\right|$ 不全为0。

构造正对角矩阵 $D_1=diag\left(d_1,d_2,\cdots ,d_n\right)$，记 $B=A{D}_1=\left(b_{ij}\right)$，其中

$d_i=\{\begin{array}{l}{x}_{1i}^{(k)},i\in N_1^{(k)}\hfill \\ x_{2i},i\in N_2\hfill \\ Q_l{\delta }_{l,i},i\in N_3\hfill \end{array}$

1) 对 $\forall i\in N_{{}_1}^{(k)}\left(k=1,2,\cdots ,m\right)$，由(6)式得

${\Lambda }_i\left(B\right)={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)},t\ne i}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|}{x}_{2t}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\le \left|a_{ii}\right|x_{1i}^{(k)}=\left|b_{ii}\right|$ ;

2) 对 $\forall i\in N_2$，由(7)式得

${\Lambda }_i\left(B\right)={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\le \left|a_{ii}\right|x_{2i}=\left|b_{ii}\right|$ ;

3) 对 $\forall i\in N_3$， $l\in Z^{+}$，由(5)式得

${\Lambda }_i\left(B\right)={\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}+Q_l{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|{\delta }_{l,t}}}\le Q_l{\delta }_{l,i}\left|a_{ii}\right|\text{=}\left|b_{ii}\right|$.

综上所述， $\left|b_{ii}\right|>{\Lambda }_i\left(B\right)\left(\forall i\in N\right)$，且至少有一个严格不等式成立。由矩阵A不可约的性质可知矩阵 $B=A{D}_1$ 不可约，所以B是不可约对角占优矩阵。所以由引理1可知 $B\in \tilde{D}$，即存在正对角阵D₂使得 $B{D}_2\in D$，则 $A\left(D_1{D}_2\right)=B{D}_2$ 为严格对角占优矩阵。由于 $D_1{D}_2$ 是正对角阵，所以A是非奇异H-矩阵。

2.3. 定理3

记 $J_1=U_{k=1}^m{J}_1^{\left(k\right)}$，其中

$J_1^{\left(k\right)}=\left\{i\in N_1^{\left(k\right)}:\left|a_{ii}\right|x_{1i}^{(k)}>{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)},t\ne i}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\right\}\left(k=1,2,\cdots ,m\right)$,

$J_2=\left\{i\in N_2:\left|a_{ii}\right|x_{2i}>{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\right\}$,

$J_3=\left\{i\in N_3:Q_l\left|a_{ii}\right|{\delta }_{l,i}>{\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3,t\ne i}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\right\}$.

定理3 设 $A\in M_n\left(C\right)$，A不可约，若存在 $l\in Z^{+}$，使得

$\left|a_{ii}\right|x_{1i}^{(k)}\ge {\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)},t\ne i}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_{{}_1}^{(k)},k=1,2,\cdots ,m\right)$, (8)

$\left|a_{ii}\right|x_{2i}\ge {\displaystyle \underset{k=1}{\overset{m}{\sum }}\left({\displaystyle \underset{t\in N_1^{(k)}}{\sum }\left|a_{it}\right|}{x}_{1t}^{(k)}\right)+}{\displaystyle \underset{t\in N_2,t\ne i}{\sum }\left|a_{it}\right|x_{2t}}+Q_l{\displaystyle \underset{t\in N_3}{\sum }\left|a_{it}\right|}{\delta }_{l,t}\left(\forall i\in N_2\right)$, (9)

且上式中至少有一个严格不等式成立，即 $J_1\cup J_2\ne \varnothing$。如果 $i\in U_{i=1}^3\left[N_i-J_i\right]$ 都有非零元素链 $a_{i{r}_1},a_{r_1{r}_2},\cdots ,a_{r_{k-1}k}$ 使得 $k\in U_{i=1}^3{J}_i$，则 $A\in \tilde{D}$。

3. 数值实例

例1 设矩阵

$A=\left(\begin{array}{cccccc}4& 1& 1& 0& 0& 2\\ 2.5& 5.5& 0& 1& 2& 0\\ 1.5& 0& 3& 1.5& 0& 2\\ 1& 0& 1& 3& 0& 5\\ 1& 1& 0& 2& 25& 6\\ 0& 0& 0.5& 0& 4.5& 15\end{array}\right)$

则在判定矩阵A是否为非奇异H-矩阵时，文 [1]，文 [2]，文 [3] 及文 [4] 的定理条件都无法判定，而用本文的判定定理可以判定。(以下计算结果均保留六位小数。)

事实上，对文 [1]，有

$\left|a_{33}\right|x_3=1.2<2.357144+\left(\underset{i\in N_3}{\max }{M}_i\right)\left|a_{36}\right|x_6$ ;

现取 $m=1$， $l=2$。

对文 [2]，有

$\left|a_{33}\right|x_3=1.2<2.357144+\left|a_{36}\right|{\delta }_{l,6}$ ;

对文 [3]，有

$\left|a_{33}\right|\frac{{\Lambda }_3-\left|a_{33}\right|}{{\Lambda }_3}=1.2<2.357144+\frac{h{P}_6}{\left|a_{66}\right|}\left|a_{36}\right|$ ;

对文 [4]，有

$\left|a_{33}\right|x_{13}=1.2<2.357144+\left|a_{36}\right|{\delta }_{2,6}$ ;

而对本文定理1，当 $m=1$ 时，即为推论1，则

$\left|a_{11}\right|x_{21}=1.880381>1.51488=\left|a_{12}\right|x_{22}+\left|a_{13}\right|x_{13}+Q_2\left|a_{16}\right|{\delta }_{2,6}$,

$\left|a_{22}\right|x_{22}=3.640229>2.261694=\left|a_{21}\right|x_{21}+\left|a_{24}\right|x_{14}+Q_2\left|a_{25}\right|{\delta }_{2,5}$,

$\left|a_{33}\right|x_{13}=2.1>2.036735=\left|a_{31}\right|x_{21}+\left|a_{34}\right|x_{14}+Q_2\left|a_{36}\right|{\delta }_{2,6}$,

$\left|a_{44}\right|x_{14}=2.357143>1.552647=\left|a_{41}\right|x_{2,2}+\left|a_{43}\right|x_{13}+Q_2\left|a_{46}\right|{\delta }_{2,6}$ ;

显然满足本文推论1的判定条件，取正对角矩阵

$X=diag\left(0.470095,0.661859,0.7,0.785714,0.150371,0.076511\right)$,

有 $AX\in D$，则矩阵A是非奇异H-矩阵。

例2 设矩阵

$A=\left(\begin{array}{cccccc}5& 2& 1& 1& 0& 1\\ 1& 4& 1& 0& 2& 0\\ 0.5& 0& 2& 1.5& 1& 1\\ 0& 0.5& 0& 2.5& 0& 5\\ 1& 1& 0& 2& 25& 5\\ 1& 0& 1& 0& 6& 20\end{array}\right)$

则在判定矩阵A是否为非奇异H-矩阵时，文 [1]，文 [2]，文 [3] 及文 [4] 的定理条件都无法判定，而用本文的判定定理可以判定。(以下计算结果均保留六位小数。)

事实上，对文 [1]，有

$\left|a_{33}\right|x_3=1<1.318182+\left(\underset{i\in N_3}{\max }{M}_i\right)\left(\left|a_{35}\right|x_5+\left|a_{36}\right|x_6\right)$ ；

现取 $m=2$， $l=1$。

对文 [2]，有

$\left|a_{33}\right|x_3=1<1.318182+\left|a_{35}\right|{\delta }_{l,5}+\left|a_{36}\right|{\delta }_{l,6}$ ;

对文 [3]，有

$\left|a_{33}\right|\frac{{\Lambda }_3-\left|a_{33}\right|}{{\Lambda }_3}=1<1.181818+\frac{h{P}_5}{\left|a_{55}\right|}\left|a_{35}\right|+\frac{h{P}_6}{\left|a_{66}\right|}\left|a_{36}\right|$ ;

对文 [4]，有

$\left|a_{44}\right|x_{14}=0.113638<0.25+\left|a_{46}\right|{\delta }_{2,6}$ ;

而对本文定理1，当 $m=2$ 时，即为推论2，则

$\left|a_{11}\right|x_{21}=3.244364>2.200322=\left|a_{12}\right|x_{22}+\left|a_{13}\right|x_{13}+\left|a_{14}\right|x_{14}+Q_1\left|a_{16}\right|{\delta }_{1,6}$,

$\left|a_{22}\right|x_{22}=2.048485>1.561094=\left|a_{21}\right|x_{21}+\left|a_{23}\right|x_{13}+Q_1\left|a_{25}\right|{\delta }_{1,5}$,

$\left|a_{33}\right|x_{13}=1.333333>1.149808=\left|a_{31}\right|x_{21}+\left|a_{34}\right|x_{14}+Q_1\left|a_{35}\right|{\delta }_{1,5}+Q_1\left|a_{36}\right|{\delta }_{1,6}$,

$\left|a_{44}\right|x_{14}=0.965909>0.871309=\left|a_{42}\right|x_{21}+Q_1\left|a_{46}\right|{\delta }_{1,6}$ ;

显然满足本文推论2的判定条件，取正对角矩阵

$X=diag\left(0.648873,0.512121,0.666667,0.386364,0.122777,0.123049\right)$,

有 $AX\in D$，则矩阵A是非奇异H-矩阵。

例3 设矩阵

$A=\left(\begin{array}{ccccccc}5& 1& 0.5& 0& 1& 1.5& 1\\ 1& 6& 0& 1& 1& 1& 2\\ 1& 2& 10& 3.5& 4.4& 1& 1.5\\ 0.5& 1.5& 3& 9& 2& 2& 2.5\\ 1& 2& 0& 1& 9& 4& 2\\ 1& 1& 0& 2& 2& 24& 2\\ 1& 0& 1& 1& 5& 4& 25\end{array}\right)$

则在判定A是否为非奇异H-矩阵时，文 [1]，文 [2]，文 [3] 及文 [4] 的定理条件都无法判定，而用本文的判定定理可以判定。(以下计算结果均保留六位小数。)

事实上，对文 [1]，有

$\left|a_{55}\right|x_5=0.9<3.217391+\left(\underset{i\in N_3}{\max }{M}_i\right)\left(\left|a_{56}\right|x_6+\left|a_{57}\right|x_7\right)$ ;

现取 $m=3$， $l=2$。

对文 [2]，有

$\left|a_{55}\right|x_5=0.9<3.217391+\left|a_{56}\right|{\delta }_{l,6}+\left|a_{57}\right|{\delta }_{l,7}$ ;

对文 [3]，有

$\left|a_{33}\right|\frac{{\Lambda }_3-\left|a_{33}\right|}{{\Lambda }_3}=2.53731<4.200869+\frac{h{P}_6}{\left|a_{66}\right|}\left|a_{36}\right|+\frac{h{P}_7}{\left|a_{77}\right|}\left|a_{37}\right|$ ;

对文 [4]，有

$\left|a_{55}\right|x_{15}=0.9<1.217391+\left|a_{56}\right|{\delta }_{2,6}+\left|a_{57}\right|{\delta }_{2,7}$ ;

而对本文定理1，当 $m=3$ 时，有

$\left|a_{11}\right|x_{21}=1.95517>1.259377=\left|a_{12}\right|x_{22}+\left|a_{13}\right|x_{13}+\left|a_{15}\right|x_{15}+Q_2\left|a_{16}\right|{\delta }_{2,6}+Q_2\left|a_{17}\right|{\delta }_{2,7}$,

$\left|a_{22}\right|x_{22}=2.236338>1.5441=\left|a_{21}\right|x_{22}+\left|a_{24}\right|x_{14}+\left|a_{25}\right|x_{15}+Q_2\left|a_{26}\right|{\delta }_{2,6}+Q_2\left|a_{27}\right|{\delta }_{2,7}$,

$\left|a_{33}\right|x_{13}=4.402985>4.356896=\left|a_{31}\right|x_{21}+\left|a_{32}\right|x_{22}+\left|a_{34}\right|x_{14}+\left|a_{35}\right|x_{15}+Q_2\left|a_{36}\right|{\delta }_{2,6}+Q_2\left|a_{37}\right|{\delta }_{2,7}$,

$\left|a_{44}\right|x_{14}=3.717391>3.34477=\left|a_{41}\right|x_{21}+\left|a_{42}\right|x_{22}+\left|a_{43}\right|x_{13}+\left|a_{45}\right|x_{15}+Q_2\left|a_{46}\right|{\delta }_{2,6}+Q_2\left|a_{47}\right|{\delta }_{2,7}$,

$\left|a_{55}\right|x_{15}=2.925>2.366521=\left|a_{51}\right|x_{21}+\left|a_{52}\right|x_{22}+\left|a_{54}\right|x_{14}+Q_2\left|a_{56}\right|{\delta }_{2,6}+Q_2\left|a_{57}\right|{\delta }_{2,7}$ ;

显然满足本文定理1的条件，取正对角矩阵

$X=diag\left(0.391034,0.372722,0.440299,0.413043,0.325,0.133992,0.140515\right)$,

有 $AX\in D$，则矩阵A是非奇异H-矩阵。

4. 结论

1) 通过例1表明，本文的迭代判定方法比文献 [1] 定理1和文献 [3] 定理1的非迭代的判定方法好，且迭代次数少于文献 [2] 和文献 [4] 定理中的迭代判定定理。

2) 通过例2表明，本文推论2和文献 [3] 定理1将非占优行指标集分为两个区间时，本文推论2的判定方法要优于文献 [3] 的定理1，且迭代一次就能判定，而文献 [2] 和文献 [4] 迭代一次时不能判定。

3) 通过例3表明，本文细分非占优行指标集区间后判定范围比文献 [3] 定理的判定范围更广，并且在m相同的情况下，本文定理1的迭代次数要少于文献 [2] 和文献 [4] 的判定定理。

因此，本文给出的非奇异H-矩阵细分迭代实用判定方法，不仅扩宽矩阵的判定范围，而且判定更高效。

致谢

感谢庹清老师对本项目的悉心指导和帮助。

基金项目

国家自然科学基金(11461027)和吉首大学校级科研项目资助(Jdy20056)。

NOTES

^*通讯作者。