摘要: 本文主要研究了一类临界增长的分数阶 Schrödinger 方程
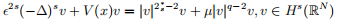
变号解的存在性,其中
0 < s < 1,N ≥ 3,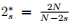
是分数阶临界指数,µ是一个正常数,
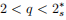
,
ε > 0是一个小参数,
V ∈ C1(RN , R)满足
a ≤ V (x) ≤ b, b > a > 0 , ∀x ∈ RN.通过临界理论和下降流不变集法,我们得到了该方程存在k对变号解.
Abstract:
In this paper, we study the following critical nonlinear fractional Schrödinger equations
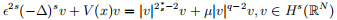
where 0 < s < 1,N ≥ 3,
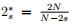
is the fractional critical exponent, µ is a normal number,
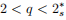
, ε > 0 is a small parameter, V ∈ C
1(R
N , R) satisfies a ≤ V (x) ≤ b, b > a > 0 , ∀x ∈ R
N . We obtain the existence of k pairs of sign-changing solutions by combining critical point theory and invariant sets of descending flow.