1. 引言
从一个代数到另一个代数的线性映射,若其保持了代数里边某些元素特性不变,则称它是一个线性保持映射。关于线性保持问题最早的论文可以追溯到1897年,此后算子空间上的线性保持问题一直受到了众多学者的广泛关注 [1] [2] [3] [4]。而其中一类算子代数von Neumann代数上的线性保持问题,国内外许多学者对其进行了研究与探索并已取得许多成果。例如:2013年齐霄霏和侯晋川在文献 [5] 中刻画了von Neumann代数上的强斜交换线性保持映射;2013年杜宁在文献 [6] 中刻画了von Neumann代数上保持自Jordan积和半*-Jordan积的映射;2016年费秀海和张建华在文献 [7] 中刻画了von Neumann代数上保持投影的映射;2018年C. Li,F. Zhao,Q. Chen在文献 [8] 中刻画了在von Neumann代数上保乘积
的映射。
受以上文献的启发,本文我们将主要研究von Neumann代数上保持绝对连续和奇异的映射。映射保持绝对连续和奇异性的相关内容在文献 [9] [10] [11] 中有学者进行过研究。我们将说明若von Neumann代数上的双射
在两个方向上都保持绝对连续,则其在两个方向上也保持奇异。并且借助有界、可逆、线性或共轭线性的算子将这个双射
完全刻画。下面先介绍一些概念并固定一些符号。
设
是一个无限维的复Hilbert空间,用
表示它上面的内积,
表示
上所有有界线性算子的全体。令
是
上的一个
-子代数,若
包含恒等算子且具有前对偶,即存在一个Banach空间
使得
的对偶空间为
,则称
为von Neumann代数。若
,(
),则称
为自伴算子。若A是自伴的且对任意的
有
成立,则称
为正算子。并用
表示所有正算子的锥。设
是一个von Neumann代数,
称为
的一秩元,如果a的值域投影
是
中的一个极小投影 [12]。
对任意
若
称为偏序,记作:
。
定义1.1:(1) 任意
,如果满足
且
的
只能是零算子,则称A和B是奇异的,记作:
。
(2) 若存在一个正算子序列
和一个非负实数序列
,满足
且
,这里
是指
单调递增且
强收敛于A,则称A是B-绝对连续的,记作:
。
下面给出一个双射在两个方向上保持绝对连续性和奇异性的定义:
定义1.2:(1) 称双射
在两个方向上保持绝对连续,如果对于任意
有,
。
(2) 称双射
在两个方向上保持奇异,如果对于任意的
有,
。
2. 主要定理及其证明
引理2.1 ( [13],引理4)对有界算子S和T,下列条件等价:
(i)
;
(ii) 存在
使得
。
定理2.1 令
,则
当且仅当
。
证明 当
,
时,有
和
均有意义,此时我们有
。由引理2.1知,存在
,使得
(这比A是B-绝对连续条件更强)。因此我们有A是B-绝对连续的。
反之,若A是B-绝对连续的,则由绝对连续的定义我们有,存在一个正算子序列
和一个非负实数序列
,满足
且
,即
。由引理2.1可知
。 □
定理2.2 令
,则
当且仅当
。
证明 对任意的
,令
,则显然有
。
反之,若
,定义
表示正算子A和B的平行和,正算子序列
是单调递增的,以B为上界,记作:
。
由文献( [13],引理4)我们有
等价于
。因此
可以推出
。□
引理2.2 ( [13],定理5)若
,则
当且仅当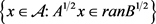 在
中稠密。
在
中稠密。
定理2.3 令
,A的值域
是闭的当且仅当
闭。
证明 对任意
,则显然有
因此,若
是闭的,则
也是闭的。
反之,若
是闭的,我们有
即
。故
是闭的。
由这个定理可知,对任意的
,若
和
是闭的,则
。 □
下面我们给出von Neumann代数上的一个双射
在两个方向上保持绝对连续和奇异的等价刻画。
定理2.4 设
是无限维复Hilbert空间上的一个von Neumann代数。
为von Neumann代数上的一个正锥。若
是一个双射,则下列四个叙述等价:
(i)
在两个方向上保持绝对连续;
(ii)
在两个方向是保持奇异;
(iii) 存在一个有界、可逆、线性或共轭线性算子
,使得对所有的
有
(iv) 存在一个有界、可逆、线性或共轭线性算子
和一族可逆正算子
,使得对所有的
有
证明 (i) Þ (ii):因为对所有的正算子B来说,0是
上唯一B-绝对连续的元。所以由(i)可知
。现假设
满足(i)但不满足(ii),则存在
使得
但
与
不垂直。特别地,在von Neumann代数中我们可以找到一个极小投影R,满足
,因此
且
又存在非零的秩一元
,使得
,从而
且
。但这表明
,因此A与B不垂直,这与假设相矛盾。
(ii) Þ (iii):对任意
,假设
且
,则由定理2.2知,
对任意的
,定义
我们有
其中
。
我们定义一个新的映射:
其中,
。
显然
有定义且是一个双射,由
和
我们可知
在这两个方向上保零交。即
其中
。
接下来我们进一步看映射
,易知
因此
在两个方向上保包含关系:
其中
。
事实上,由以上两式我们有
且
。注意到
对任意正整数n,令
,则当
限制到
时是
到自身的一个双射。类似地,我们有:
从而,
也是一个双射。由以上结论我们可得
是一个射影,且
可以将任何三个共面元素映成共面元素。因此应用射影几何的基本定理可以得到:存在一个半线性映射
使得
其中
。
接下来我们考虑
作用到更一般的
。通过上边的性质,对任意的
和
,我们有
和
因此,对所有的
我们有
进而,通过
和T的定义我们有对任意的
,
接下来我们的主要任务就是证明半线性映射T是有界的、线性或共轭线性的。由于T和
将一余维线性流形映射为一余维线性流形。此外,
的有限余维子空间是一个算子值域当且仅当它是闭的,因此我们推断定T将
映射到
上。由于
是无限维的,我们可以使用文献 [14] 的引理2及其推论,得出T是线性或共轭线性的。
最后,为了证明T是有界的,只需证明对于每一个有界线性泛函
使得
,这意味着存在
使得
,因此
是有界的。用类似的方法我们可以证明T是共轭线性的。
(iii) Þ (iv):首先,假设T是线性的。由于对任意的
,
,因此可得
其中
。
从而,由( [15],推论1)知,存在一个可逆算子
,使得
。进而,令
,则(iv)成立。
假设现在T是共轭线性的,考虑任意一个反酉算子
,则
其中
。
(iv) Þ (i):由于对任意的
,
,故对任意的
,我们有
因此由文献( [15],推论4)可知,存在一个可逆算子
使得
记
其中
。
通过计算我们有:
由此可知
稠当且仅当
是稠的。进而由引理2.2可知(i)成立。□
如果
是有限维的Hilbert空间,那么上面的定理2.4的证明将会更简单。然而,我们需要指出的是在有限维情形下,此时T没有必要是线性或者共轭线性的。下面我们给出具体的定理:
定理2.5 设
是有限维复Hilbert空间且
,
是
上的一个von Neumann代数。
为von Neumann代数上的一个正锥。若
是一个双射,则下列叙述等价:
(i)
在两个方向上保持绝对连续;
(ii)
在两个方向是保持奇异;
(iii) 存在一个半线性双射
使得对任意的
。
最后需要注意的是定理2.5中不包含
的情形,因此此时我们不能再应用射影几何的基本定理。
致谢
本文作者衷心感谢审稿人和读者的意见和建议。
基金项目
国家自然科学基金资助项目(11801397);国家留学基金管理委员会资助项目(202006935001)。