Bazykin捕食系统的平衡点和余维2 Bogdanov-Takens分支：全局渐近稳定性

Equilibria and Bogdanov-Takens Bifurcation of Codimension 2 of the Bazykin’s Predator-Prey System: Global Asymptotic Stability

摘要: 本文从一个全局渐近稳定性定理出发讨论了Bazykin捕食系统，并在特定参数条件下给出若干内平衡点和一个余维2 BT分支，包括重数为1的多重焦点、余维2尖点和余维3 Bogdanov-Takens奇点(焦点或中心)。最后，结合数值类比，系统经历相应的余维2 Bogdanov-Takens分支。

Abstract: This paper discusses the Bazykin’s predator-prey system from a globally asymptotically stable theorem, and presents several interior equilibria and a Bogdanov-Takens bifurcation of codimension 2 under certain parameter conditions, including multiple focus of multiplicity one, cusp of codimension 2 and Bogdanov-Takens singularity of codimension 3 (focus or center). Finally, combining numerical simulations, this system undergoes the corresponding codimension 2 Bogdanov-Takens bifurcation.

1. 引言

本文考虑具有Holling II功能反应的Bazykin捕食系统 [1] [2]：

$\stackrel{\dot{}}{x}=r_{1}x\left(1-\frac{x}{K_1}\right)-\frac{\alpha xy}{a+x}-m_{1}x,$ (1.1a)

$\stackrel{\dot{}}{y}=\frac{\alpha exy}{a+x}-m_{2}y-d{y}^2,$ (1.1b)

这里 $x=x\left(t\right)$ 和 $y=y\left(t\right)$ 分别表示食饵和捕食者在时间 $t$ 的种群密度，初始条件为 $x\left(0\right)$， $y\left(0\right)>0$，其它正的常数有其各自的生物学意义，即： $r_1$ 表示食饵 $x$ 的内禀增长率， $K_1$ 表示环境承载能力常数， $\alpha$ 表示捕食者对食饵的捕获效率， $a$ 是半饱和常数， $e$ 是生物量转化系数， $m_1$ 和 $m_2$ 分别表示食饵和捕食者各

自的死亡率， $d$ 是捕食者的种间竞争系数。 $r_1\left(1-\frac{x}{K_1}\right)$ 表示食饵在缺乏捕食者时的增长情况， $d{y}^2$ 表示捕食者种间密度限制情况， $\frac{\alpha x}{a+x}$ 称为Holling II功能反应，最初由C.S. Holling提出，描述了捕食者如何将

食饵转化为自身种群增长所需 [3] [4] [5] [6]。当 $d=0$ 时，系统退化为Rosenzweig-MacArthur (R-M)模型 [7] [8] [9]。显然系统(1.1)满足上述初始条件的解是非负一致有界的，因此第一象限是其正向不变集。

对于系统(1.1)，在一些文献中已经进行了深入研究。如A.D. Bazykin在文献 [2] 中详细讨论了平衡点的稳定性，极限环的全局存在性，平衡点的全局吸引，Hopf分支及余维2分支。在 [10] 中，作者通过特定变换研究该系统局部稳定性的解析描述和变化。在文献 [11] 中，作者研究了一个种群具有自我抑制的类似Lotka-Volterra系统的全局稳定性和极限环存在性：

$\stackrel{\dot{}}{x}=x\left(1-k_{1}x-k_2{x}^2\right)-\frac{xy}{1+ax},$ (1.2a)

$\stackrel{\dot{}}{y}=\frac{rxy}{1+ax}-y\left({\delta }_0+{\delta }_{1}y\right),$ (1.2b)

并利用Poincare-Bendixson理论的思想详细且定性地证明了至少存在两个极限环。显然，除去某些参数外系统(1.2)在 $k_2=0$ 时将简化为上述系统，而这又在文献 [12] 及 [13] 中分析了平衡点的稳定性，Hopf分支，全局吸引和余维2分支。文献 [14] 则研究了系统(1.1)的全局行为。在 [15] 中考虑了带有常数反馈m的

修正Holling II功能反应 $\frac{\beta \left(x-m\right)}{1+\alpha \left(x-m\right)}$，作者给出了关于内平衡点全局稳定性及稳定极限环存在唯一性的

充分性条件。

本文将从一个全局渐近稳定性定理出发重新考虑Bazykin捕食系统(1.1)，安排如下。首先给出内平衡点的存在性条件，如重数为1的多重焦点，余维2尖点和余维3 BT奇点(焦点或中心)，其次讨论了取特定参数条件下一类余维2 Bogdanov-Takens (BT)分支，最后是总结和讨论。此外，相应的数值类比支持了本文的结论。

2. 平衡点的分析

2.1. 予备工作：一个全局渐近稳定性定理

本节首先通过构造一个定正Lyapunov函数 $V\left(x,y\right)=\left(x-x_{*}-x_{*}\ln \frac{x}{x_{*}}\right)+\frac{a+x_{*}}{ae}\left(y-y_{*}-y_{*}\ln \frac{y}{y_{*}}\right)$ 来说

明内平衡点 $E_{*}=\left(x_{*},y_{*}\right)$ 的全局渐近稳定性 [16]。

定理1：若系统(1)存在唯一的内平衡点 $E_{*}=\left(x_{*},y_{*}\right)$，且参数满足 $\frac{\alpha y_{*}}{a\left(a+x_{*}\right)}<\frac{r_1}{K_1}$，则 $E_{*}$ 是全局渐近

稳定的(双曲型焦点或结点)。 ■

对于一般性条件 $\frac{\alpha y_{*}}{a\left(a+x_{*}\right)}\le \frac{r_1}{K_1}$，则 $E_{*}$ 是局部渐近稳定的焦点或结点。引入参数变换 $m_2=\lambda \alpha e$， $K_1=\frac{\mu a{r}_1}{\alpha e}$ 和控制变量 $\lambda \in \left(0,1\right)$， $\mu >0$， $\rho \in \left(0,1\right]$，得到相应的内平衡点 $E_{*}=\left(x_{*},y_{*}\right)$ 和参数限制条件：

$x_{*}=\frac{a\left[\mu \left(r_1-m_1\right)-\alpha \rho e\right]}{\alpha e},y_{*}=\frac{\left[\mu \left(r_1-m_1\right)+\alpha e\left(1-\rho \right)\right]\rho a}{\mu \alpha },$ (2.1a)

$d=\frac{{\alpha }^{2}e\mu \left[\left(1-\lambda \right)\left(r_1-m_1\right)\mu +\alpha e\left(\left(\rho -1\right)\lambda -\rho \right)\right]}{a\rho {\left[\alpha e\left(1-\rho \right)+\mu \left(r_1-m_1\right)\right]}^2},$ (2.1b)

这要求 $\mu \left(r_1-m_1\right)>\alpha e\left(\rho +\frac{\lambda }{1-\lambda }\right)$。取参数值为 $r_1=0.6$， $m_1=0.2$， $m_2=0.1$， $\alpha =0.5$， $a=\text{1}.\text{5}$， $K_1=20$，

$e=0.\text{6}$ 和 $\rho =0.9$，图1描述了一个全局渐近稳定结点。

本文将进一步考虑 $\rho >1$ 的情形，此时内平衡点 $E_{*}=\left(x_{*},y_{*}\right)$ 形式上仍不变。系统(1.1)在 $E_{*}$ 处Jacobi矩阵 $J\left(E_{*}\right)$ 的迹，行列式和判别式分别记为 $A_1=trJ\left(E_{*}\right)$， $A_2=\det J\left(E_{*}\right)$ 和 ${\Delta }_{\text{*}}=A_1^2-4A_2$。对于一般的双曲型奇点 $E_{*}$，其稳定性和类型已经由一次线性近似理论确定，不做详述。

2.2. 多重焦点(中心–焦点问题)

对于条件(2.1)，为使得Jacobi矩阵 $J\left(E_{*}\right)$ 具有一对共轭纯虚的零实部本征值，令 $A_1=0$，即

$\lambda ={\lambda }^H:=\frac{\left[\alpha \rho e+\mu \left(m_1-r_1\right)\right]\left[\left(\alpha e-m_1+r_1\right)\mu -\alpha e\left(2\rho -1\right)\right]}{\left[\alpha e\left(\rho -1\right)+\mu \left(m_1-r_1\right)\right]\alpha e\mu },$ (2.2)

相应的平衡点表达式(2.1a)形式不变，而参数条件(2.1b)为

$d=\frac{\alpha \left[\alpha e\left(2\rho -1\right)+\mu \left(m_1-r_1\right)\right]\left[\mu \left(r_1-m_1\right)-\alpha \rho e\right]}{a\rho {\left[\alpha e\left(1-\rho \right)+\mu \left(r_1-m_1\right)\right]}^2}$。 (2.3)

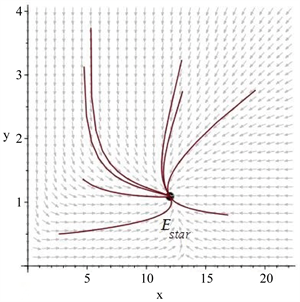
Figure 1. A globally asymptotically stable node

图1. 一个全局渐近稳定的结点

此时 $A_2=\frac{\mu \left(r_1-m_1\right)-\alpha \rho e}{{\left[\mu \left(r_1-m_1\right)-\alpha e\left(\rho -\text{1}\right)\right]}^2{\mu }^2}{\phi }_{A_2}\left(\mu ,\rho \right)$，其中辅助函数

$\begin{array}{l}{\phi }_{A_2}\left(\mu ,\rho \right)={\left(m_1-r_1\right)}^3{\mu }^3+\alpha e\left(5\rho -2\right){\left(m_1-r_1\right)}^2{\mu }^2+{\alpha }^2{e}^2\\ \left[\alpha e\rho +\left(2\rho -1\right)\left(4\rho -1\right)\left(m_1-r_1\right)\right]\mu +{\alpha }^3{e}^3\rho {\left(2\rho -1\right)}^2。\end{array}$ (2.4)

如果 $A_2<0$，则 $E_{*}$ 是鞍点。如果 $A_2>0$，矩阵 $J\left(E_{*}\right)$ 具有一对共轭纯虚本征值，化为中心–焦点问题，

此时利用变换 $x=u+x_{*}$， $y=v+y_{\text{*}}$ 将点 $E_{\text{*}}$ 平移至原点O，再取变量变换 $u=-d{y}_{\text{*}}X+\beta Y$， $v=-\frac{\alpha ea{y}_{\text{*}}}{{\left(a+x_{\text{*}}\right)}^2}X$，

其中 $\beta =\sqrt{A_2\left(E_{\text{*}}\right)}>0$，将系统(1.1)化为标准形式：

$\stackrel{\dot{}}{X}=-\beta Y+{\displaystyle \underset{i+j=2}{\overset{3}{\sum }}{a}_{ij}{X}^i{Y}^j+O\left({\left|X,Y\right|}^4\right)},Y=\beta X+{\displaystyle \underset{i+j=2}{\overset{3}{\sum }}{b}_{ij}{X}^i{Y}^j+O\left({\left|X,Y\right|}^4\right)}$。 (2.5)

按照 [17] [18] [19]，上述系统的第一Lyapunov数为

$\begin{array}{l}\sigma =\frac{\text{3}\pi }{\text{2}\beta }\left\{\text{3}\left(a_{30}+b_{03}\right)+\left(a_{12}+b_{21}\right)-\frac{1}{\beta }\left[2\left(a_{20}{b}_{20}-a_{02}{b}_{02}\right)-a_{11}\left(a_{02}+a_{20}\right)+b_{11}\left(b_{02}+b_{20}\right)\right]\right\}\\ =\frac{\text{3}\pi {\alpha }^5{e}^5\rho \left[\alpha \rho e+\mu \left(m_1-r_1\right)\right]{\phi }_{\sigma }\left(\mu ,\rho \right)}{2{\mu }^2{a}^2\beta {\left[\alpha e\left(\rho -1\right)+\mu \left(m_1-r_1\right)\right]}^5{\phi }_{A_2}\left(\mu ,\rho \right)},\end{array}$ (2.6)

其中辅助函数 ${\phi }_{\sigma }\left(\mu ,\rho \right)={\displaystyle \underset{k=0}{\overset{5}{\sum }}{A}_{\sigma ,k}\left(\rho \right){\mu }^k}$，系数 $A_{\sigma ,k}=A_{\sigma ,k}\left(\rho \right)$ 为

$A_{\sigma ,0}={\alpha }^5{e}^5{\rho }^2\left(2{\rho }^2-6\rho +3\right)\left(2\rho -1\right),$

$A_{\sigma ,1}={\alpha }^4{e}^4\rho \left[18\left(m_1-r_1\right){\rho }^3+4\left(\alpha e-11m_1+11r_1\right){\rho }^2+\left(28m_1-28r_1-3\alpha e\right)\rho +5\left(r_1-m_1\right)\right],$

$A_{\sigma ,2}={\alpha }^3{e}^3\left(m_1-r_1\right)\left[\text{32}\left(m_1-r_1\right){\rho }^3+\left(53r_1-53m_1+9\alpha e\right){\rho }^2+\left(22m_1-22r_1-7\alpha e\right)\rho +\text{2}\alpha \text{e}+\text{2}{r}_1-2m_1\right],$

$A_{\sigma ,3}={\alpha }^2{e}^2{\left(r_1-m_1\right)}^2\left[28\left(m_1-r_1\right){\rho }^2+\left(7\alpha e+29r_1-29m_1\right)\rho +6m_1-6r_1-4\alpha e\right],$

$A_{\sigma ,4}=2\alpha e{\left(r_1-m_1\right)}^3\left[6\left(m_1-r_1\right)\rho +3\left(r_1-m_1\right)+\alpha e\right],$

$A_{\sigma ,5}=2{\left(m_1-r_1\right)}^5$。

利用变换 $u=\beta X+d{y}_{\text{*}}Y$， $v=\frac{\alpha ea{y}_{\text{*}}}{{\left(a+x_{\text{*}}\right)}^2}Y$ 也可得到公式(2.6)中的 $\sigma$。显然 $\sigma$ 的符号由函数 ${\phi }_{\sigma }\left(\mu ,\rho \right)$ 决定。

当 $\sigma <0\left(>0\right)$ 时， $E_{*}$ 是重数为1的稳定(不稳定)多重焦点，相应的非退化Hopf分支是超临界(次临界)的，并且由此临界平衡点分支出的极限环是稳定(不稳定)的。当 $\sigma =0$ 时，需进一步计算第二Lyapunov系数，可能出现Bautin分支(广义Hopf分支)。

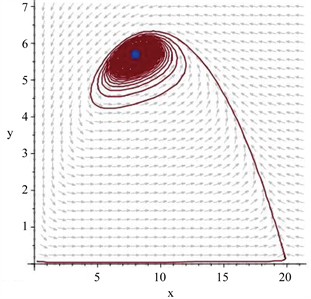
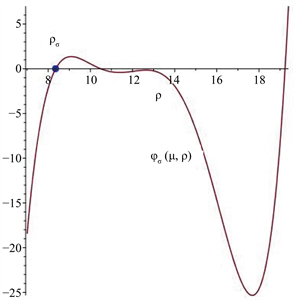
例1：首先取参数值为 $r_1=0.7$， $m_1=0.2$， $a=\text{1}.\text{5}$， $\alpha =0.5$， $e=0.\text{6}$ 和 $\mu =8$，结合图2(a)中函数 ${\phi }_{\sigma }\left(\mu ,\rho \right)$ 的图象，分别取 $\rho =8$ 和 $\rho =8.5$ 得到稳定和不稳定的多重焦点，详见图3。注意当变量 $\rho$ 较大时，如 $\rho =19$，上述 ${\lambda }^H\left(<0\right)$ 不存在。当 $\rho ={\rho }_{\sigma }\approx \text{8}.\text{35}0\text{246}$ 时 $\sigma =0$，此时出现一条半稳定极限环，见图2(b)。

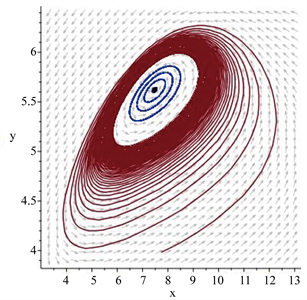(a) (b)

Figure 2. (a) Curve of function ${\phi }_{\sigma }\left(\mu ,\rho \right)$ ; (b) A semi-stable limit cycle

图2. (a) 函数 ${\phi }_{\sigma }\left(\mu ,\rho \right)$ 的图象；(b) 半稳定极限环

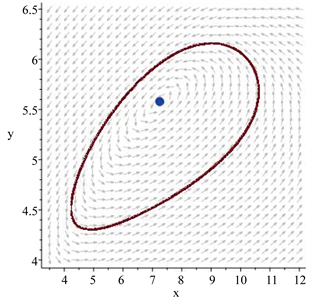(a) (b)

Figure 3. Multiple foci with multiplicity one: (a) stable; (b) unstable: limit cycle

图3. 重数为1的多重焦点：(a) 稳定；(b) 不稳定：极限环

2.3. 余维2和余维3尖点

对于上一小节中 $A_1=0$ 的情形，如果还有 $A_2=0$，即由(2.4)得到方程 ${\phi }_{A_2}\left(\mu ,\rho \right)=0$ 及临界值 ${\mu }^{BT}$。

在上述参数条件下先取变换(I)： $x=X+x_{\text{*}}$， $y=Y+y_{\text{*}}$，将系统(1.1)化为

$\stackrel{\dot{}}{X}=F_1\left(X,Y\right),\stackrel{\dot{}}{Y}=G_1\left(X,Y\right),$ (2.7)

再取变换

(II)： $u=Y$， $v=\frac{-{\left(m_1-r_1\right)}^2{\mu }^{2}Y-\alpha e\mu \left(3\rho -1\right)\left(m_1-r_1\right)Y-{\alpha }^2{e}^2\rho \left(\left(2\rho -1\right)Y+eX\right)}{\left[\alpha e\left(\rho -1\right)+\mu \left(m_1-r_1\right)\right]\mu }$，

将上述系统化为标准形式

$\stackrel{\dot{}}{u}=F_2\left(u,v\right)=v+a_{20}{u}^2+a_{11}uv+a_{02}{v}^2+O\left({\left|u,v\right|}^3\right),$ (2.8a)

$\stackrel{\dot{}}{v}=G_2\left(u,v\right)=b_{20}{u}^2+b_{11}uv+b_{02}{v}^2+O\left(|u,v{|}^3\right)$。 (2.8b)

利用 [20] 中的引理1或通过一系列变换，系统(2.8)拓扑等价于

$\stackrel{\dot{}}{x}=y,\stackrel{\dot{}}{y}=d_1{x}^2+d_{2}xy+O\left({\left|x,y\right|}^3\right),$ (2.9)

其中 $d_1=b_{20}$ 和 $d_2=b_{11}+2a_{20}$ 为相应的判别式，即

$d_1=\frac{\alpha \left[\mu \left(r_1-m_1\right)-\alpha e\rho \right]\left[\left(m_1-r_1\right)\mu +\alpha e\left(2\rho -1\right)\right]{\phi }_{d_1}\left(\mu ,\rho \right)}{a{\mu }^2{\left[\alpha e\left(\rho -1\right)+\mu \left(m_1-r_1\right)\right]}^3},$ (2.10a)

$d_2=\frac{{\phi }_{d_2}\left(\mu ,\rho \right)}{a\mu \rho e{\left[\alpha e\left(\rho -1\right)+\mu \left(m_1-r_1\right)\right]}^2},$ (2.10b)

其中辅助函数 ${\phi }_{d_1}\left(\mu ,\rho \right)={\displaystyle \underset{k=0}{\overset{2}{\sum }}{A}_{d_1,k}\left(\rho \right){\mu }^k}$， ${\phi }_{d_2}\left(\mu ,\rho \right)={\displaystyle \underset{k=0}{\overset{3}{\sum }}{A}_{d_2,k}\left(\rho \right){\mu }^k}$，系数 $A_{d_l,k}=A_{d_l,k}\left(\rho \right)$， $l=1,2$ 为

$A_{d_1,0}={\alpha }^2{e}^2\rho \left(2\rho -1\right)\left(1-\rho \right),$

$A_{d_1,1}=\alpha e\left[3\left(r_1-m_1\right){\rho }^2+\left(\alpha e+4m_1-4r_1\right)\rho -m_1+r_1\right],$

$A_{d_1,2}=\left(m_1-r_1\right)\left[2\alpha e+\left(1-\rho \right)\left(m_1-r_1\right)\right],$

$A_{d_2,0}=2{\alpha }^3{e}^3\rho \left(2\rho -1\right)\left({\rho }^2-3\rho +1\right),$

$A_{d_2,1}=2{\alpha }^2{e}^2\left[3\left(m_1-r_1\right){\rho }^3+\left(\alpha e-12m_1+12r_1\right){\rho }^2+\left(7m_1-7r_1-\alpha e\right)\rho +r_1-m_1\right],$

$A_{d_2,2}=\alpha e\left(m_1-r_1\right)\left[2\left(m_1-r_1\right){\rho }^2+\left(\alpha e-12m_1+12r_1\right)\rho -\alpha e+4m_1-4r_1\right],$

$A_{d_2,3}={\left(r_1-m_1\right)}^2\left(\alpha e-2m_1+2r_1\right)$。

当 $d_1{d}_2\ne 0$ 时， $E_{*}$ 是余维2尖点。进一步的，如果令 $d_1=0$，不难得到内平衡点 $E_{*}=\left(\frac{\left(\rho -2\right)a}{2},\frac{4ae\rho }{\rho -2}\right)$

和参数条件为

${\lambda }^{BT}=\frac{\rho -6}{\rho },{\mu }^{BT}=\frac{1}{8}\rho \left(\rho -2\right),r_1=\frac{m_1{\rho }^2+\left(12\alpha e-2m_1\right)\rho -8\alpha e}{\rho \left(\rho -2\right)},d=\frac{\left(\rho -2\right)\alpha }{a{\rho }^2}。$ (2.11)

此时 $d_2=\frac{\left(14-5\rho \right)\alpha }{a{\rho }^2}\ne 0$，因 $\rho >6$。这样 $E_{*}$ 是余维3尖点。事实上，通过下列变换

$\left(\text{II}\right):u=-\frac{54\left(\rho -2\right)X}{\alpha a{\left(3\rho -2\right)}^2}-\frac{18\left(\rho -2\right)Y}{a\alpha e{\left(3\rho -2\right)}^2},v=-\frac{72eX}{\rho a\left(3\rho -2\right)}+\frac{18\left(\rho -2\right)Y}{\rho a\left(3\rho -2\right)},$

$\left(\text{III}\right):u=p,v=q-a_{20}{p}^2-a_{02}{q}^2,$

$\left(\text{IV}\right):p=w+\frac{1}{2}{d}_{02}{w}^2,q=d_{02}wz+z。$

系统(2.7)最终化为标准形式

$\stackrel{\dot{}}{w}=z+{\displaystyle \underset{i+j=3}{\overset{}{\sum }}{e}_{ij}{w}^i{z}^j}+O\left({\left|w,z\right|}^{\text{4}}\right),$ (2.12a)

$\stackrel{\dot{}}{z}=f_{11}wz+{\displaystyle \underset{i+j=3}{\overset{}{\sum }}{f}_{ij}{w}^i{z}^j}+O\left({\left|w,z\right|}^{\text{4}}\right),$ (2.12b)

其中 $f_{11}=b_{11}+2a_{20}\ne 0$， $f_{30}<0$ 及

$\text{5}{f}_{30}\left(f_{\text{2}1}+\text{3}{e}_{30}\right)-3f_{11}\left(f_{40}-e_{30}{f}_{11}\right)=\frac{32{\alpha }^{\text{7}}{e}^3{\left(3\rho -2\right)}^4\left(5{\rho }^2+12\rho -28\right)}{\text{6}561{\rho }^7{\left(\rho -2\right)}^2}\ne 0$，

$f_{11}^2+8f_{30}=-\frac{4{\alpha }^4{e}^2{\left(3\rho -2\right)}^2\left(7{\rho }^2+12\rho -68\right)}{81{\rho }^4{\left(\rho -2\right)}^2}<0$，

因此 $E_{*}$ 是余维3 BT奇点(焦点或中心) [21]。

定理2：在参数条件(2.11)下，相应的平衡点 $E_{*}$ 是余维3 BT奇点(焦点或中心)。 ■

例2：这里取 $m_1=r_1-\frac{3}{4}\alpha e$， $\rho =\frac{15}{2}+\frac{3}{2}\sqrt{21}$， ${\lambda }^H=\frac{5\sqrt{21}-21}{4}$， ${\mu }^{BT}=12+\frac{8}{3}\sqrt{21}$，以保证关于 $\mu$ 的三次方程 ${\phi }_{A_2}\left(\mu ,\rho \right)=0$ 仅有两个实根，则 $d_1=\frac{3\left(19\sqrt{21}-87\right){\alpha }^{2}e}{8a}$， $d_2=\frac{\left(35\sqrt{21}-159\right)\alpha }{6a}$，平衡点 $E_{\text{*}}^{(2)}=\left(\frac{\left(3+\sqrt{21}\right)a}{2}，\frac{3\left(3+\sqrt{21}\right)ae}{8}\right)$ 是余维2尖点，另一个平衡点 $E_{*}^{\left(1\right)}=\left(\left(\sqrt{21}+4\right)a,\frac{\left(3+\sqrt{21}\right)ae}{2}\right)$ 是渐近稳

定的双曲型结点。见图4(a)，其中参数取值为 $r_1=1$， $\alpha =0.5$， $a=\text{1}.\text{5}$ 及 $e=0.\text{6}$。

对于余维3 BT奇点情形，取参数值为 $m_1=0.2$， $\rho =7$， $\alpha =0.5$， $a=\text{1}.\text{5}$ 及 $e=0.\text{6}$，图4(b)给出相应的相图。

3. 余维2 Bogdanov-Takens分支

在上一节例2的基础上，本节考虑相应的Bogdanov-Takens分支。选取 $m_2$ 和d为BT分支参数，并引入充分小参数矢量 $\delta =\left({\delta }_1,{\delta }_2\right)$，考虑如下开折系统：

$\stackrel{\dot{}}{x}=r_{1}x\left(1-\frac{x}{K_1}\right)-\frac{\alpha xy}{a+x}-m_{1}x,$ (3.1a)

$\stackrel{\dot{}}{y}=\frac{\alpha exy}{a+x}-\left(m_2+{\delta }_1\right)y-\left(d+{\delta }_2\right)y^2。$ (3.1b)

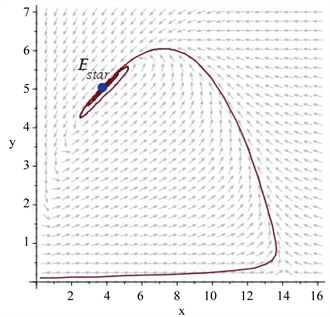(a) (b)

Figure 4. (a) A cusp of codimension 2 $E_{*}^{\left(2\right)}$ and an asymptotic stable node $E_{*}^{\left(1\right)}$ ; (b) A BT singularity of codimension 3

图4. (a) 余维2尖点 $E_{*}^{\left(2\right)}$ 和渐近稳定结点 $E_{*}^{\left(1\right)}$ ；(b) 余维3 BT奇点(焦点)

首先取线性变换将平衡点移至原点O：

$\stackrel{\dot{}}{X}=F_1\left(X,Y\right)={\displaystyle \underset{i+j=0}{\overset{2}{\sum }}{a}_{ij}\left(\delta \right)X^i{Y}^j+O\left({\left|X,Y\right|}^3\right)},$ (3.2a)

$\stackrel{\dot{}}{Y}=G_1\left(X,Y\right)={\displaystyle \underset{i+j=0}{\overset{2}{\sum }}{b}_{ij}\left(\delta \right)X^i{Y}^j+O\left({\left|X,Y\right|}^3\right)},$ (3.2b)

再取变换(II)： $u=X,v=F_1\left(X,Y\right)$，上述系统化为

$\stackrel{\dot{}}{u}=F_2\left(u,v\right)=v,$ (3.3a)

$\stackrel{\dot{}}{v}=G_2\left(u,v\right)={\displaystyle \underset{i+j=0}{\overset{2}{\sum }}{d}_{ij}\left(\delta \right)}{u}^i{v}^j+O\left({\left|u,v\right|}^{\text{3}}\right),$ (3.3b)

然后取变换(III)： $p=u+\frac{d_{01}\left(\delta \right)}{d_{11}\left(\delta \right)},q=v$，又有以下系统：

$\stackrel{\dot{}}{p}=F_3\left(p,q\right)=q,$ (3.4a)

$\stackrel{\dot{}}{q}=G_{\text{3}}\left(u,v\right)={\displaystyle \underset{i+j=0}{\overset{2}{\sum }}{f}_{ij}\left(\delta \right)}{p}^i{q}^j+O\left({\left|p,q\right|}^{\text{3}}\right)$。 (3.4b)

令变换(IV)为： $w=p,z=\left(1-f_{02}\left(\delta \right)p\right)q,dt=\left(1-f_{02}\left(\delta \right)p\right)d\tau$，并将符号 $\tau$ 记为 $t$，得到新的系统

$\stackrel{\dot{}}{w}=F_{\text{4}}\left(w,z\right)=z,$ (3.5a)

$\stackrel{\dot{}}{z}=G_{\text{4}}\left(w,z\right)={\displaystyle \underset{i+j=0}{\overset{2}{\sum }}{h}_{ij}\left(\delta \right)}{w}^i{z}^j+O\left({\left|w,z\right|}^{\text{3}}\right)$。 (3.5b)

注意 $h_{20}\left(\text{0},0\right)>0$ 且 $h_{11}\left(0,0\right)=d_{11}\left(0,0\right)\ne 0$，因此当 $\delta$ 在原点的某个小邻域内变化时 $h_{20}\left(\delta \right)>0$ 且 $h_{\text{11}}\left(\delta \right)\ne 0$。

最后，构造变换(V)： $x_1=\frac{h_{11}{\left(\delta \right)}^2}{h_{20}\left(\delta \right)}w,y_1=\frac{h_{11}{\left(\delta \right)}^3}{h_{20}{\left(\delta \right)}^2}z$， $dt=\frac{h_{11}\left(\delta \right)}{h_{20}\left(\delta \right)}d\tau$，并且仍将符号 $\tau$ 写为 $t$，则上述系统化为

${\stackrel{\dot{}}{x}}_1=F_{\text{5}}\left(x_1,y_1\right)=y_1,$ (3.6a)

${\stackrel{\dot{}}{y}}_1=G_{\text{5}}\left(x_1,y_1\right)=d_1\left(\delta \right)+d_2\left(\delta \right)x_1+x_1^2+x_1{y}_1+O\left({\left|x_1,y_1\right|}^{\text{3}}\right),$ (3.6b)

其中

$d_{\text{1}}=d_{\text{1}}\left(\delta \right)=\frac{8\left(1375+28\sqrt{21}\right)}{81\alpha e}{\delta }_1+\frac{\left(4713+1459\sqrt{21}\right)a}{27\alpha }{\delta }_2+O\left({\left|{\delta }_1,{\delta }_2\right|}^2\right),$ (3.7a)

$d_{\text{2}}=d_{\text{2}}\left(\delta \right)=-\frac{4\left(170+41\sqrt{21}\right)}{27\alpha e}{\delta }_1-\frac{\left(\text{401}+\text{83}\sqrt{21}\right)a}{6\alpha }{\delta }_2+O\left({\left|{\delta }_1,{\delta }_2\right|}^2\right),$ (3.7b)

以及

${\frac{-1}{\frac{\partial d_1}{\partial {\delta }_2}}\cdot \frac{\partial \left(d_{\text{1}},d_{\text{2}}\right)}{\partial \left({\delta }_{\text{1}},{\delta }_{\text{2}}\right)}|}_{\delta =\text{0}}=-\frac{4\left(35+3\sqrt{21}\right)}{27\alpha e}<0,$ (3.8)

因此系统(3.1)在余维2尖点处是generic family开折的，并且有展开至二阶项的分支曲线局部近似表示

[22]，而原点处近似直线的斜率为 $k_{BT}=\frac{2\left(3-\sqrt{21}\right)}{9ae}<0$。

(i) 鞍–结分支(SN)曲线为

$\begin{array}{l}SN=\left\{\delta |d_{\text{1}}=\frac{\text{1}}{\text{4}}{d}_{\text{2}}^{\text{2}}\right\}\\ =\{\delta |\frac{\text{8}\left(\text{1375}+\text{28}\sqrt{\text{21}}\right)}{\text{81}\alpha e}{\delta }_1+\frac{\left(\text{4713}+\text{1459}\sqrt{\text{21}}\right)a}{\text{2}7\alpha }{\delta }_2-\frac{4\left(5791+12422\sqrt{\text{21}}\right)}{729{\alpha }^2{e}^2}{\delta }_{\text{1}}^{\text{2}}\\ +\frac{\left(125897+33987\sqrt{\text{21}}\right)a}{81{\alpha }^{2}e}{\delta }_1{\delta }_2+\frac{\left(414325+88561\sqrt{\text{21}}\right)a^2}{72{\alpha }^2}{\delta }_2^2+O\left({\left|{\delta }_1,{\delta }_2\right|}^3\right)=0\}；\end{array}$ (3.9)

(ii) Hopf分支(Hopf)曲线为

$\begin{array}{l}Hopf=\left\{\delta |d_{\text{1}}=0,d_2<0\right\}\\ =\{\delta |\frac{8\left(1375+28\sqrt{\text{21}}\right)}{81\alpha e}{\delta }_1+\frac{\left(4713+1459\sqrt{\text{21}}\right)a}{27\alpha }{\delta }_2+\frac{88\left(885+23\sqrt{\text{21}}\right)}{243{\alpha }^2{e}^2}{\delta }_{\text{1}}^{\text{2}}\\ +\frac{2\left(132765+32269\sqrt{\text{21}}\right)a}{81{\alpha }^{2}e}{\delta }_1{\delta }_2+\frac{\left(141765+30461\sqrt{\text{21}}\right)a^2}{18{\alpha }^2}{\delta }_2^2+O\left({\left|{\delta }_1,{\delta }_2\right|}^3\right)=0\}；\end{array}$ (3.10)

(iii) 同宿分支(HL)曲线为

$\begin{array}{l}HL=\left\{\delta |d_{\text{1}}=-\frac{6}{25}{d}_2^2,d_2<0\right\}\\ =\{\delta |\frac{8\left(1375+28\sqrt{\text{21}}\right)}{81\alpha e}{\delta }_1+\frac{\left(4713+1459\sqrt{\text{21}}\right)a}{27\alpha }{\delta }_2+\frac{8\left(\text{500179+62085}\sqrt{\text{21}}\right)}{6075{\alpha }^2{e}^2}{\delta }_{\text{1}}^{\text{2}}\\ +\frac{2\left(4994721+1173337\sqrt{\text{21}}\right)a}{2025{\alpha }^{2}e}{\delta }_1{\delta }_2+\frac{37\left(120555+25979\sqrt{\text{21}}\right)a^2}{450{\alpha }^2}{\delta }_2^2+O\left({\left|{\delta }_1,{\delta }_2\right|}^3\right)=0\}。\end{array}$ (3.11)

定理3：对于系统(3.1)及例2中的参数条件，如果取分支参数为 $m_2$ 和 $d$，对于平衡点 $E_{\text{*}}^{\left(2\right)}$，当参数 $\delta$ 在原点的某个小邻域内变化时，存在某些参数值使得系统(3.1)出现余维2 Bogdanov-Takens分支。 ■

例3：按照2.2小节中的例取参数值，有如下鞍–结(红色)，Hopf (绿色)及同宿(蓝色)分支曲线图(见图5)，并将该邻域划分为若干子区域，使得在每个子区域上系统(3.1)展示出不同的动力学行为。叙述如下。

Figure 5. Curves of saddle-node (red), Hopf (green) and homoclinic (blue) bifurcations

图5. 鞍–结(红色)，Hopf (绿色)及同宿(蓝色)分支曲线

(i) 当 $\delta =0$ 时，存在一个余维2尖点 $E_{\text{*}}^{\left(2\right)}$ 和一个渐近稳定的结点 $E_{\text{*}}^{\left(1\right)}$，见2.2节例2；

(ii) 当 $\delta =\left(0.0001,-\text{1}\text{.953216}\times {\text{10}}^{-\text{5}}\right)$，即参数 $\delta$ 落在区域I上时，存在一个不稳定焦点，一个鞍点和一个稳定结点，(iii)中的同宿环破缺；

(iii) 当参数 $\delta$ 落在同宿分支曲线上时，存在一个不稳定的焦点，一个鞍点和一个稳定结点，以及一条同宿环；

(iv) 当 $\delta =\left(0.0001,-\text{3}\text{.906377}\times {\text{10}}^{-\text{5}}\right)$，即参数 $\delta$ 落在区域II上时，存在一个不稳定的焦点，一个鞍点和一个稳定结点；

(v) 当参数 $\delta$ 落在Hopf分支曲线上时，存在一个鞍点和一个稳定结点，以及一个非双曲点(具有一对共轭纯虚本征值)；

(vi) 当 $\delta =\left(0.0001,-\text{3}\text{.906266}\times {\text{10}}^{-\text{5}}\right)$，即参数 $\delta$ 落在区域III上时，存在一个稳定的焦点，一个鞍点和一个稳定结点，结合(iv)知这保证了Hopf分支；

(vii) 当 ${\delta }_1=0.0001$， ${\delta }_2=0$，即参数 $\delta$ 落在区域IV上时，存在唯一的稳定结点；

(viii) 当参数 $\delta$ 落在鞍–结分支曲线 $S{N}_1$ 上时，存在三个内平衡点；

(ix) 当参数 $\delta$ 落在鞍–结分支曲线 $S{N}_2$ 上时，存在唯一的稳定结点。

最后考虑取参数条件(2.2)~(2.4)时系统(3.1)的非退化Hopf分支存在曲线，引入 $x=x_{*}+w$， $\left|w\right|\ll 1$，计算 $A_1=0$ 及 $A_2>0$ 可得 ${\delta }_1\left(w\right)$ 和 ${\delta }_2\left(w\right)$，即

$\begin{array}{c}{\delta }_1=\frac{w\alpha e}{\mu a\left[e\left(\rho -1\right)\alpha +\mu \left(m_1-r_1\right)\right]\left[\left(\left(\rho -1\right)a-w\right)e\alpha +\mu a\left(m_1-r_1\right)\right]}\\ \left[\left(\left(2{\rho }^2+\mu -4\rho +1\right)a-2w\left(\rho -1\right)\right)e^2{\alpha }^2+4\mu \left(\left(\rho -3/4\right)a-\left(1/2\right)w\right)\left(m_1-r_1\right)e\alpha +2a{\mu }^2{\left(m_1-r_1\right)}^2\right],\end{array}$ (3.12a)

$\begin{array}{c}{\delta }_2=\frac{-1}{a{\left[e\left(\rho -1\right)\alpha +\mu \left(m_1-r_1\right)\right]}^2\rho \left(a\rho -w\right){\left[\left(\left(\rho -1\right)a-w\right)e\alpha +\mu a\left(m_1-r_1\right)\right]}^2}\\ [2w\alpha (\left(\left({\rho }^2-\rho \right)a-w\left(\rho -1/2\right)\right)\rho \left(a\rho -w\right)e^4{\alpha }^4+3\mu \left(\left({\rho }^2-\left(2/3\right)\rho +1/3\right)a-w\left(\rho -1/3\right)\right)\\ \left(\left(\rho -1/2\right)a-\left(1/2\right)w\right)\left(m_1-r_1\right)e^3{\alpha }^3+\left(7/2\right){\mu }^2{\left(m_1-r_1\right)}^2\\ \left(\left({\rho }^2-\left(8/7\right)\rho +3/7\right)a^2-w\left(\rho -4/7\right)a+\left(1/7\right)w^2\right)e^2{\alpha }^2\\ +2{\mu }^3\left(\left(\rho -3/4\right)a-\left(1/2\right)w\right)a{\left(m_1-r_1\right)}^{3}e\alpha +\left(1/2\right)a^2{\mu }^4{\left(m_1-r_1\right)}^4)]。\end{array}$ (3.12b)

因此系统(3.1)的Hopf分支存在曲线定义为

$Hp=\left\{\delta |\left({\delta }_1,{\delta }_2\right)满足(3.12),A_2>0\right\},$ (3.13)

并且曲线Hp在参数平面上原点O处某邻域内近似为一条直线，其斜率为 $k_{Hp}=\underset{w\to 0}{\lim }\frac{{\delta }_2\left(w\right)}{{\delta }_1\left(w\right)}$，即

$k_{Hp}=\frac{\left[{\left(m_1-r_1\right)}^3{\mu }^3+\alpha e\left(3\rho -2\right){\left(m_1-r_1\right)}^2{\mu }^2+{\alpha }^2{e}^2\left(4{\rho }^2-3\rho +1\right)\left(m_1-r_1\right)\mu +\text{2}{\alpha }^3{e}^3{\rho }^3\right]\mu }{ae{\rho }^2\left[\alpha e\left(1-\rho \right)+\mu \left(r_1-m_1\right)\right]\left[2{\left(m_1-r_1\right)}^2{\mu }^2+\alpha e\left(\alpha e+\left(4\rho -3\right)\left(m_1-r_1\right)\right)\mu +{\alpha }^2{e}^2\left(2{\rho }^2-4\rho +1\right)\right]}。$ (3.14)

显然在例2的参数条件下，斜率 $k_{Hp}$ 退化为 $k_{BT}$。按例2的参数值，图6是相应的Hopf分支存在曲线，将参数平面划分为I，II两个区域。当参数 $\delta$ 分别落在区域I，II上时，相应平衡点分别为稳定的焦点和不稳定焦点，后者导致极限环产生。

Figure 6. Hopf (Hp) bifurcation curve

图6. Hopf (Hp)分支曲线

4. 总结与讨论

对于一般复杂的非线性捕食生态模型，往往难以求得内平衡点的解析表达式 [19]。本文从一个全局渐近稳定性定理出发给出了特定参数条件下的一类内平衡点，而不是首先从Jacobi矩阵本征值为零的角度出发进行求解。从代数学上看，我们获得了平衡点所满足的代数方程的一类特殊解。通过计算又得到了余维3 BT奇点(焦点或中心)，这与用内平衡点分量 $x_{*}$ 或 $y_{*}$ 所满足三次方程的判别式或者直接使用等价系统判断 $d_1{d}_2$ 相比较，所得结果一致。这启示我们，某种程度上表明了系统(1.1)中余维3尖点的唯一性，以及余维 $N\left(\ge 4\right)$ 尖点的不存在性，这是今后要考虑的问题(P1)。另外，对于一般的非奇异变量变换，系统(1.1)具有何种不变量或守恒量是一个需要深入思考的问题(P2)，如细焦点的Lyapunov系数或焦点量，余维2尖点的“指标” $\mathrm{sgn}\left(d_1{d}_2\right)=\pm 1$，等等。

对于一些复杂的临界情况暂未予以考虑，如 $\sigma =0$ 时的细焦点分析和退化Hopf分支，一般 $d_1{d}_2\ne 0$ 时的余维2 BT分支曲线，前者需进一步考虑更烦琐的高阶焦点量或Lyapunov系数，但后者可以参考第3节的方法，同时注意对余维2尖点进行分类。2.2小节表明了所得余维2尖点的存在性，第3节表明了这一类余维2 BT分支的存在性。至于由2.2小节引出的余维3退化焦点型BT分支，也可以得到，如取 $r_1$， $K_1$ 和 $d$ 为分支参数 [6] [23]。第3节给出的Hopf分支存在曲线与斜率 $k_{Hp}$ 似乎表明，当 $\mu \to {\mu }^{BT}$ 时，BT分支是Hopf分支的极限情况，这也是今后需要考虑的问题(P3)。最后本文所用方法对于其它捕食模型仍然具有参考意义，如 [19]。

致谢

作者感谢编辑的细致工作，感谢审稿人所提的宝贵建议，感谢赵敏老师和戴传军老师。

基金项目

国家自然科学基金面上项目(31570364)；国家自然科学基金(61871293)；国家重点研发计划“政府间国际科技创新合作/港澳台科技创新合作”重点专项项目(2018YFE0103700)。