带积分边界条件的非线性二阶常微分方程多个正解的存在性
Existence of Multiple Positive Solutions for Nonlinear Second-Order Ordinary Differential Equations with Integral Boundary Conditions
DOI: 10.12677/PM.2021.116121, PDF,    国家自然科学基金支持
作者: 康慧君：西北师范大学数学与统计学院，甘肃 兰州
关键词: 积分边界条件；二阶；多个正解；Krasnoselskii’s不动点定理；Integral Boundary Conditions； Second-Order； Multiple Positive Solutions； Krasnoselskii’s Fixed Point Theorem
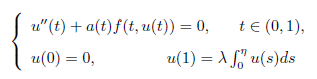
摘要: 运用锥上的 Krasnoselskii’s 不动点定理,考虑了二阶积分边值问题 多个正解的存在性,其中0 < η < 1是常数,0 < λ < 2/n2是参数,f:[0,1]×[0,∞)→[0,∞)是连续函数,a:[0,1]→[0,+∞)是连续函数,且在[0,1]的任一子区间上不恒为零.
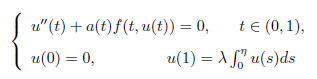
Abstract: In this paper, we study existence of multiple positive solutions for second-order ordinary differential equations with integral boundary problem by the Krasnoselskii’s fixed point theorem on cones. where 0 < η < 1 is a constant, 0 < λ < 2/n2 is a parameter, f:[0,1]×[0,∞)→[0,∞) is continuous, a:[0,1]→[0,+∞) is continuous, and a(t) ≢ 0 on any subinterval of [0,1].
文章引用：康慧君. 带积分边界条件的非线性二阶常微分方程多个正解的存在性[J]. 理论数学, 2021, 11(6): 1067-1075. https://doi.org/10.12677/PM.2021.116121

参考文献

[1] I1’in, M. (1987) Nonlocal Boundary-Value Problem of the First Kind for a Sturm-Liouville Operator in Its Differential and Finite Difference Aspects. Differential Equations, 23, 803-810.
[2] Yao, Z.J. (2015) New Results of Positive Solutions for Second-Order Nonlinear Three-Point Integral Boundary Value Problems. Journal of Nonlinear Science Applications, 8, 93-98.
[3] Zhai, C.B. (2009) Positive Solution for Semi-Positone Three-Point Boundary Value Problems. Journal of Computational and Applied Mathematics, 228, 279-286.
https://doi.org/10.1016/j.cam.2008.09.019
[4] Han, X.L. (2007) Positive Solution for a Three-Point Boundary Value Problems. Nonlinear Analysis: Theory, Methods and Applications, 66, 679-688.
https://doi.org/10.1016/j.na.2005.12.009
[5] Li, J.L. and Shen, J.H. (2006) Multiple Positive Solutions for a Second-Order Three-Point Boundary Value Problems. Applied Mathematics and Computation, 182, 258-268.
https://doi.org/10.1016/j.amc.2006.01.095
[6] Ma, R.Y. (2001) Positive Solutions for Second-Order Three-Point Boundary Value Problems. Applied Mathematics Letters, 14, 1-5.
https://doi.org/10.1016/S0893-9659(00)00102-6
[7] Xu, X. (2004) Multiplicity Results for Positive Solutions of Some Semi-Positone Three-Point Boundary Value Problems. Journal of Mathematical Analysis Applications, 291, 673-689.
https://doi.org/10.1016/j.jmaa.2003.11.037
[8] Gupta, C.P. (1992) Solvability of a Three-Point Nonlinear Boundary Value Problem for a Second Order Ordinary Differential Equations. Journal of Mathematical Analysis Applications, 168, 540-551.
https://doi.org/10.1016/0022-247X(92)90179-H
[9] Feng, W.Y. and Wdbb, J.R.L. (1997) Solvability of an m-Point Nonlinear Boundary Value Problem with Nonlinear Growth. Journal of Mathematical Analysis Applications, 212, 467- 480.
https://doi.org/10.1006/jmaa.1997.5520
[10] Jessada, T. (2010) Positive Solutions of a Nonlinear Three-Point Integral Boundary Value Problem. Boundary Value Problem, 519, 210-221.

为你推荐