具有对抗性节点的多智能体系统的固定时间准包围控制

Fixed-Time Quasi-Containment Control of Multi-Agent Systems with Antagonistic Nodes

摘要: 本文研究了具有对抗性节点的多智能体系统的固定时间准包围控制问题。基于代数图论和固定时间稳定性定理，通过设计一个新的控制协议，具有对抗性节点的多智能体系统可以在有限时间内实现准包围控制。同时给出了多智能体系统实现固定时间准包围控制的稳定时间上界估计式。最后通过Matlab仿真，验证了所获理论结果的有效性。

Abstract: In this paper, the problem of fixed-time quasi-containment control for multi-agent systems with antagonistic nodes is studied. Based on algebraic graph theory and fixed-time stability theorem, by designing a new control protocol, multi-agent systems with antagonistic nodes can realize qua-si-containment control in finite time. Moreover, the upper bound estimation of the settling time for multi-agent systems to realize fixed-time quasi-containment control is given. Finally, the validity of the theoretical results is verified by Matlab simulation.

1. 引言

在自然界中，我们经常看到迁徙的大雁群，共筑巢穴的蜜蜂群，以及协同搬运食物的蚂蚁群等一致性的行为。尽管每个生物体自身的能力有限，但是通过合作却能够创造出超越个体能力之和的总价值。多智能体系统 [1] 的思想正来源于此，并在一致性控制问题 [2]、编队控制 [3]、包围控制 [4]、群集控制 [5] 等方面展开深入的研究。

包围控制是指通过利用合适的算法，驱使所有跟随者的状态最终进入到由领导者所产生的凸包内。它具有更广泛的工程应用价值。例如，当航空母舰在海上航行时，护航舰队们利用包围控制算法将航母包围在中间，以保护航母。正是由于包围控制在具体的工程应用上具有广泛的价值，从而引起了学者们的研究热潮。如在文献 [6] 中，作者通过自适应内部模型和递归稳定控制律，提出了一种分布式包围控制方案，使得智能体能够进入到由领导者所形成的凸包内。文献 [7] 针对具有输入饱和的线性多智能体系统，通过一种新的低增益反馈方法，分别提出了状态反馈和输出反馈包围控制协议。文献 [8] 讨论了具有有向交互拓扑的时滞高阶线性时不变多智能体系统的编队包围控制问题，并将时滞多智能体系统的编队包围控制问题转化为时滞系统的渐近稳定性问题。在文献 [9] 中，作者研究了具有通信时变时滞的一般线性多智能体系统的包围控制问题。基于有向交互拓扑，给出了反馈控制器存在的一些充分条件，保证了所需的控制效果。

值得一提的是，现有的研究大多集中在多智能体系统的渐近收敛问题上。然而，在实际应用中，通常要求系统高效地完成给定的任务。在这种情况下，渐近收敛不足以满足要求，因此需要研究具有更好收敛特性的有限时间问题。例如，在文献 [10] 中，作者研究了具有不确定非线性动态和有向通信约束的多网络系统的编队包围控制问题，并提出了一种分布式自适应有限时间控制方法。文献 [11] 中的工作考虑了具有完全未知输入的虚拟领导者的二阶多智能体系统的有限时间编队包围跟踪问题，并引入了三层递阶结构。这些结果表明，尽管有限时间稳定性具有更好的收敛特性，但是系统的初始值会影响收敛时间的上界。此外，在实际应用中很难获得系统的初始值。基于此，大量学者对固定时间包围控制问题进行了研究，如在文献 [12] 中，作者介绍了有向拓扑下网络化非线性系统的分布式固定时间包围控制问题，并首次提出了一种无连续控制更新的分布式事件触发控制协议。文献 [13] 中，作者提出了一种分布式固定时间控制协议，在固定的交互拓扑上引导领导者达成外部一致，并使得所有跟随者进入领导者形成的凸包。

与现有的包围控制问题不同的是，本文给出的场景中的一些领导者与邻居有着相反的表现，我们称这类问题为准包围控制问题。在多智能体系统中，以相反的状态欺骗他人的节点称为对抗性节点。它是从一个群体中的一些个体为了增强感染力或避免与主流观点的差异而隐藏真实观点并表达修正观点的普遍情况下抽象出来的。具有对抗性节点的系统表现出与普通系统完全不同的进化轨迹。据我们所知，在对抗性节点存在的情况下，固定时间控制问题很少被考虑。受文献 [13] 的启发，本文使用了一种新的方法，证明了在所设计的控制协议下，具有对抗性节点的多智能体系统可以在固定时间内实现给定的准包围控制，并且给出了多智能体系统实现准包围控制的稳定时间上界估计式。

2. 预备知识

2.1. 符号说明

记符号 $1_N$ 为所有元素都为1的 $N$ 行1列的实向量， $I_N$ 为 $N$ 维单位矩阵。 $\text{R}>0\left(\text{R}\ge 0\right)$ 表示所有正(非

负)实数的集合， $A^{\text{T}}$ 表示矩阵或向量 $A$ 的转置。 $diag\left(a_1,\cdots ,a_N\right)\left(或diag\left({\left[a_1,\cdots ,a_N\right]}^{\text{T}}\right)\right)$ 为对角元素是

$a_1,a_2,\cdots ,a_N$ 的对角矩阵。 $|\cdot |$ 和 $\Vert \cdot \Vert$ 分别表示标量的绝对值和向量的2范数， $sign(\cdot )$ 表示标准符号函数。对于 $\theta ={\left[{\theta }_1,{\theta }_2,\cdots ,{\theta }_N\right]}^{\text{T}}$ 和 $\alpha \in \text{R}>0$，令 $\text{sig}{\left(\theta \right)}^{\alpha }={\left[\text{sig}{\left({\theta }_1\right)}^{\alpha },\text{sig}{\left({\theta }_2\right)}^{\alpha },\cdots ,\text{sig}{\left({\theta }_N\right)}^{\alpha }\right]}^{\text{T}}$，其中 $\text{sig}{\left({\theta }_i\right)}^{\alpha }=sign\left({\theta }_i\right){\left|{\theta }_i\right|}^{\alpha }$，则

$\frac{\text{d}}{\text{d}\theta }{\left|\theta \right|}^{\alpha +1}=\left(\alpha +1\right)\text{sig}{\left(\theta \right)}^{\alpha },$

$\frac{\text{d}}{\text{d}\theta }\text{sig}{\left(\theta \right)}^{{}^{\alpha +1}}=\left(\alpha +1\right){\left|\theta \right|}^{\alpha }.$

记 ${\lambda }_1\left(A\right)\le {\lambda }_2\left(A\right)\le \cdots \le {\lambda }_N\left(A\right)$ 为 $A$ 的 $N$ 个按升序排列的特征值，其中 $A\in {\text{R}}^{N\times N}$ 为Hermitian矩阵。

2.2. 图论

用 $\mathcal{G}=\left\{V,\mathcal{E}\right\}$ 来表示交互拓扑图，其中 $V=\left\{v_1,v_2,\cdots ,v_N\right\}$ 表示图中所有节点的集合，

$\mathcal{E}\subseteq \left\{\left(v_i,v_j\right):v_i,v_j\in V\right\}$ 表示图中所有边的集合。两个节点 $i$ 和 $j$ 之间的连接权重用 $a_{ij}$ 表示，权重矩阵用

$A=\left[a_{ij}\right]\in {\text{R}}^{N\times N}$ 表示。如果节点 $i$ 和节点 $j$ 之间存在边，即 $\left(v_i,v_j\right)\in \mathcal{E}$，则 $a_{ij}\ge 0$，否则 $a_{ij}=0$。本文不考虑自循环的情形，即 $a_{ii}=0,i=1,\cdots ,N$。将度矩阵 $D$ 定义为 $D=diag\left(d_{11},d_{22},\cdots ,d_{NN}\right)$，其中 $d_{ii}={\displaystyle {\sum }_{j=1}^N{a}_{ij}}$，与图 $\mathcal{G}$ 相关的Laplacian矩阵定义为 $L=D-A$。

有向边 $\left(v_i,v_j\right)\in \mathcal{E}$ 意味着智能体 $j$ 可以从智能体 $i$ 接收信息，并且智能体 $i$ 称为智能体 $j$ 的邻居。记

$N_i=\left\{j:\left(v_i,v_j\right)\in \mathcal{E}\right\}$ 为节点 $i$ 的相邻节点的集合。图的一条从 $v_s$ 到 $v_r$ 的有向路径是指一个有序序列

$\left(v_{i_k},v_{i_{k+1}}\right)\in \mathcal{E},k=1,\cdots ,l-1$，其中 $i_1=s,i_l=r$。此外，如果对任意两个不同的节点存在有向路径，则称该图是强连通的。

2.3. 一些定义与引理

定义2.3.1 [14]：考虑一个非线性系统

$\stackrel{\dot{}}{x}\left(t\right)=f\left(x\left(t\right)\right),x\left(0\right)=x_0,$ (1)

其中 $x\in {\text{R}}^N$ 表示系统的状态变量， $f:{\text{R}}^N\to {\text{R}}^N$ 表示非线性向量场。

如果方程(1)的任何解 $x\left(t,x_0\right)$ 满足下列条件

(i) Lyapunov稳定：对于任意 $\epsilon >0$，存在 $\delta =\delta \left(\epsilon \right)>0$，使得 $\Vert x\left(t,x_0\right)\Vert <\epsilon$，其中 $\Vert x_0\Vert \le \delta$， $t\ge 0.$

(ii) 有限时间收敛：存在稳定时间函数 $T:{\text{R}}^N\backslash \left\{0\right\}\to \left(0,+\infty \right)$，使得 ${\lim }_{t\to T\left(x_0\right)}x\left(t,x_0\right)=0$，且对所有 $t\ge T\left(x_0\right)$， $x\left(t,x_0\right)=0$.

我们称系统(1)的原点是全局有限时间稳定的。

定义2.3.2 [14]：如果系统(1)的原点是全局有限时间稳定的，且对任意 $x_0\in {\text{R}}^N$，稳定时间函数 $T\left(x_0\right)$ 有界，即存在 $T_{\max }>0$，使得对所有 $x_0\in {\text{R}}^N$， $T\left(x_0\right)\le T_{\max }$，我们称系统(1)的原点是固定时间稳定的。

引理2.3.1 [15]：考虑一个标量系统

$\stackrel{\dot{}}{y}=-\alpha y^{\frac{m}{n}}-\beta y^{\frac{p}{q}}-\gamma y,y\left(0\right)=y_0,$ (2)

其中 $m,n,p,q$ 均为正奇数，且满足 $m<n,p>q$，以及 $\alpha ,\beta ,\gamma >0$。那么上述等式全局有限时间稳定，且固定时间的上界为

$T=\frac{n}{\gamma \left(n-m\right)}\ln \left(1+\frac{\gamma }{\alpha }\right)+\frac{q}{\beta \left(p-q\right)}.$

引理2.3.2 [16]：若 $a_i>0,i=1,2,\cdots ,N$，且 $0<p\le 1,q>1$，则

$\begin{array}{l}{\left({\displaystyle \underset{i=1}{\overset{N}{\sum }}{a}_i}\right)}^p\le {\displaystyle \underset{i=1}{\overset{N}{\sum }}{a}_i^p},\\ N^{1-q}{\left({\displaystyle \underset{i=1}{\overset{N}{\sum }}{a}_i}\right)}^q\le {\displaystyle \underset{i=1}{\overset{N}{\sum }}{a}_i^q}\text{.}\end{array}$

引理2.3.3 [13]：如果一个与Laplacian矩阵 $L\in {\text{R}}^{N\times N}$ 相关的有向图 $\mathcal{G}$ 是强连通的，则存在一个正列向

量 $w={\left[w_1,w_2,\cdots ,w_N\right]}^{\text{T}}$ 满足 $w^{\text{T}}{1}_N=1$ 和 $w^{\text{T}}L=0$。此外，取 $W=diag\left(w\right)$，则 $\tilde{L}=L^{\text{T}}WWL$ 和 $\hat{L}=\frac{1}{2}\left(WL+L^{\text{T}}W\right)$

是与某些无向图(分别记为 $\tilde{\mathcal{G}}$ 和 $\hat{\mathcal{G}}$ )相关的有效Laplacian矩阵，且对任意 $\vartheta \in {\text{R}}^N$，下列不等式成立

$\begin{array}{l}{\vartheta }^{\text{T}}\tilde{L}\vartheta \ge \frac{4}{N^2{\bar{d}}^2}{\vartheta }^{\text{T}}\vartheta ,\\ {\vartheta }^{\text{T}}\hat{L}\vartheta \le 2\bar{d}{\vartheta }^{\text{T}}\vartheta ,\end{array}$

其中， $\bar{d}$ 表示图 $\mathcal{G}$ 的最大度数。

3. 问题表述

考虑一个由 $N$ 个智能体组成的多智能体系统，第 $i$ 个智能体的动力学行为用下式描述：

${\stackrel{\dot{}}{x}}_i=u_i,i\in \text{Γ}=\left\{1,2,\cdots ,N\right\}.$ (3)

其中 $x_i\in \text{R}$ 表示第 $i$ 个智能体的状态， $u_i\in \text{R}$ 表示第 $i$ 个智能体的控制输入。

构造控制协议的表达式为

$\{\begin{array}{c}{u}_i=-{\rho }_i\text{sig}{\left({\tilde{y}}_i\right)}^{\alpha }-k_i\text{sig}{\left({\tilde{y}}_i\right)}^{\beta }-{\xi }_i\text{sig}\left({\tilde{y}}_i\right),i\in {\text{Γ}}_l,\\ u_i=-{\rho }_i\text{sig}{\left(y_i\right)}^{\alpha }-k_i\text{sig}{\left(y_i\right)}^{\beta }-{\xi }_i\text{sig}\left(y_i\right),i\in {\text{Γ}}_f\text{.}\end{array}$ (4)

其中

$\text{Γ}={\text{Γ}}_l\cup {\text{Γ}}_f$，其中 ${\text{Γ}}_l=\left\{1,2,\cdots ,M\right\}$ 和 ${\text{Γ}}_f=\left\{M+1,M+2,\cdots ,N\right\}$ 分别表示领导者和跟随者的集合。并且 $\alpha \in \left(0,1\right),\beta \in \left(1,+\infty \right)$， ${\delta }_i$ 为标度参数， ${\delta }_i<0$ 表示对抗性节点， ${\delta }_i>0$ 表示合作节点， ${\rho }_i,k_i,{\xi }_i,i\in \text{Γ}$ 与 ${\delta }_i$ 具有相同的符号。

定义3.1 [13]：如果对于任意初始状态 $x_i\left(0\right)\in U\subset \text{R}$，存在一个独立于 $x_i\left(0\right)$ 的标量 $T^{\text{*}}>0$，使得方程(3)的解 $x_i\left(t\right)$ 满足下列条件

$\{\begin{array}{l}\underset{t\to T^{*}}{\lim }\Vert {\delta }_i{x}_i\left(t\right)-{\delta }_j{x}_j\left(t\right)\Vert =0,t\in \left[0,T^{*}\right),i,j\in {\Gamma }_l,\hfill \\ \underset{t\to T^{*}}{\lim }\Vert {\delta }_i{x}_i\left(t\right)-x_j\left(t\right)\Vert =0,t\in \left[0,T^{*}\right),i\in {\Gamma }_l,j\in {\Gamma }_f,\hfill \\ \Vert {\delta }_i{x}_i\left(t\right)-{\delta }_j{x}_j\left(t\right)\Vert =0,t\in \left[T^{*},\infty \right),i,j\in {\Gamma }_l,\hfill \\ \Vert {\delta }_i{x}_i\left(t\right)-x_j\left(t\right)\Vert =0,t\in \left[T^{*},\infty \right),i\in {\Gamma }_l,j\in {\Gamma }_f.\hfill \end{array}$

其中 $T^{\text{*}}$ 称为稳定时间。我们称系统(3)可以实现固定时间准包围控制。此外，当 $U=\text{R}$ 时，固定时间准包围控制问题是全局求解的。

在定义3.1中， $x_i\left(t\right)$ 和 ${\delta }_i{x}_i\left(t\right)$ 分别表示智能体 $i$ 的内部状态和外部状态。其中，领导者为自己隐藏内部状态 $x_i\left(t\right)$，并将唯一的外部状态 ${\delta }_i{x}_i\left(t\right)$ 表示给其他智能体，而跟随者则基于外部状态的错误蜂拥而至。控制协议的设计是为了消除外部状态的偏差。值得注意的是，当 ${\delta }_i$ 的绝对值相同时，将实现双边一致，当 ${\delta }_i$ 的值被分成类时，将实现集群一致。更一般而言，外部状态会达成一致，称为外部一致，而内部状态只能由外部状态间接地描述。跟随者的内部状态和外部状态是相等的，即 ${\delta }_i=1,i\in {\text{Γ}}_f$。因此，跟随者将会达成一致，并以领导者的外部状态为目标。

4. 主要结果

为使得多智能体系统能够实现固定时间准包围控制，本文给出以下假设：

假设4.1:与领导者相关联的子图是强连通的，并且对于每个跟随者，至少存在一条从领导者到该节点的有向路径。其中，跟随者会受领导者的影响，反之不成立。

根据拓扑学中的假设，Laplacian矩阵显然具有如下形式

$L=\left[\begin{array}{cc}{L}_l& 0\\ L_c& L_f\end{array}\right],$ (5)

其中 $L_l$ 表示领导者之间的信息交流， $L_f$ 表示跟随者之间的信息交流， $L_c$ 为领导者对跟随者的影响。

引理4.1 [17]：在假设4.1下， $L_f$ 的所有特征值都具有正实部。

由于领导者不受跟随者的影响，故收敛分析只需证明领导者达成外部一致和在假设领导者的状态不变的情况下，所有跟随者的状态最终收敛到由领导者所产生的凸包内即可。

为简明起见，记 $x_l={\left[x_1,x_2,\cdots ,x_M\right]}^{\text{T}}$ 和 $x_f={\left[x_{M+1},x_{M+2},\cdots ,x_N\right]}^{\text{T}}$ 分别表示领导者和跟随者的状态集合。

定理4.1：如果假设4.1成立，那么系统(3)在协议(4)下可以实现固定时间准包围控制。

证明：考虑以下候选的Lyapunov函数：

$V_1={\displaystyle \underset{i=1}{\overset{M}{\sum }}{\displaystyle \underset{j=1}{\overset{M}{\sum }}{w}_i{a}_{ij}{\left({\delta }_i{x}_i-{\delta }_j{x}_j\right)}^2}}.$ (6)

其中， $w_i$ 在引理2.3.3中定义。显然， $V_1$ 是正定的，径向无界的。通过引理2.3.2和 $w_i\le 1$ 的性质，我们可以得出 $V_1$ 沿闭环系统轨迹的时间导数为

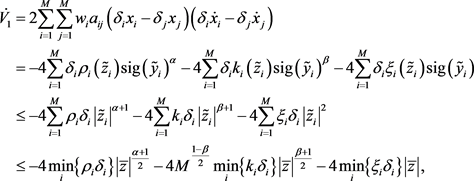
其中

通过引理2.3.3，我们可以得出

$\begin{array}{c}\Psi \triangleq \frac{{\displaystyle {\sum }_{i=1}^M{\left({\displaystyle {\sum }_{j=1}^M{w}_i{a}_{ij}\left({\delta }_i{x}_i-{\delta }_j{x}_j\right)}\right)}^2}}{{\displaystyle {\sum }_{i=1}^M{{\displaystyle {\sum }_{j=1}^M{w}_i{a}_{ij}\left({\delta }_i{x}_i-{\delta }_j{x}_j\right)}}^2}}\\ =\frac{x_l^{\text{T}}{\delta }^{\text{T}}{L}_l^{\text{T}}WW{L}_l\delta x_l}{x_l^{\text{T}}{\delta }^{\text{T}}\frac{1}{2}\left(W{L}_l+L_l^{\text{T}}W\right)\delta x_l}\\ \ge \frac{2}{N^2{\bar{d}}^3}\triangleq \varsigma \text{.}\end{array}$

其中 $\delta =diag\left({\delta }_1,{\delta }_2,\cdots ,{\delta }_M\right),\bar{d}=\underset{{}_{i\in {\text{Γ}}_l}}{\max }\left\{d_i\right\}$。为方便起见，令 $c_1=\underset{i\in {\text{Γ}}_l}{\min }\left\{{\rho }_i{\delta }_i\right\}{\varsigma }^{\frac{\alpha +1}{2}}$， $c_2=M^{\frac{1-\beta }{2}}\underset{i\in {\text{Γ}}_l}{\min }\left\{k_i{\delta }_i\right\}{\varsigma }^{\frac{\beta +1}{2}}$， $c_3=\underset{i\in {\text{Γ}}_l}{\min }\left\{{\xi }_i{\delta }_i\right\}\varsigma$.在 ${\stackrel{\dot{}}{V}}_1$ 中替换 $\Psi$ 的结果，可得到

${\stackrel{\dot{}}{V}}_1\le -4c_1{V}_1^{\frac{\alpha +1}{2}}-4c_2{V}_1^{\frac{\beta +1}{2}}-4c_3{V}_1\text{.}$ (7)

这给出了引理2.3.1的直接结果，即领导者可以在 $T_1^{\text{*}}$ 时达成一致

$T_1^{\text{*}}=\frac{1}{2c_3\left(1-\alpha \right)}\ln \left(1+\frac{c_3}{c_1}\right)+\frac{1}{2c_2\left(\beta -1\right)}.$ (8)

在我们分析跟随者的收敛之前，我们假设领导者已经达成了外部一致。记 $y={\left[y_{M+1},y_{M+2},\cdots ,y_N\right]}^{\text{T}}$。然后， $y=L_c\delta x_l+L_f{x}_f$，并且还具有 ${\stackrel{\dot{}}{x}}_f=-{\rho }_f\text{sig}{\left(y\right)}^{\alpha }-k_f\text{sig}{\left(y\right)}^{\beta }-{\xi }_f\text{sig}\left(y\right)$，其中

${\rho }_f={\left[{\rho }_{M+1},{\rho }_{M+2},\cdots ,{\rho }_N\right]}^{\text{T}}$， $k_f={\left[k_{M+1},k_{M+2},\cdots ,k_N\right]}^{\text{T}}$， ${\xi }_f={\left[l_{M+1},l_{M+2},\cdots ,l_N\right]}^{\text{T}}$。按照相同的步骤，考虑以下候选的Lyapunov函数：

$V_2=y^{\text{T}}Py\text{.}$ (9)

其中 $P$ 是 $P{L}_f+L_f^{\text{T}}P=2I_{N-M}$ 的解，且引理4.1使得 $P>0$。显然， $V_2>0$，且它是径向无界的。由于 ${\stackrel{\dot{}}{x}}_l=0$，因此 $V_2$ 关于时间的导数为

$\begin{array}{c}{\stackrel{\dot{}}{V}}_2=2y^{\text{T}}P\stackrel{\dot{}}{y}\\ =y^{\text{T}}\left(P{L}_f+L_f^{\text{T}}P\right)\left(-{\rho }_f\text{sig}{\left(y\right)}^{\alpha }-k_f\text{sig}{\left(y\right)}^{\beta }-{\xi }_f\text{sig}\left(y\right)\right)\\ =-2y^{\text{T}}{\rho }_f\text{sig}{\left(y\right)}^{\alpha }-2y^{\text{T}}{k}_f\text{sig}{\left(y\right)}^{\beta }-2y^{\text{T}}{\xi }_f\text{sig}\left(y\right)\\ =-2{\displaystyle \underset{i=M+1}{\overset{N}{\sum }}{\rho }_i{\left|y_i\right|}^{\alpha +1}}-2{\displaystyle \underset{i=M+1}{\overset{N}{\sum }}{k}_i{\left|y_i\right|}^{\beta +1}}-2{\displaystyle \underset{i=M+1}{\overset{N}{\sum }}{\xi }_i{\left|y_i\right|}^2}\text{.}\end{array}$

重复上述证明，并注意到 $V_2\le \lambda y^{\text{T}}y=\lambda {\displaystyle \underset{i=M+1}{\overset{N}{\sum }}{\left|y_i\right|}^2}$，其中 $\lambda ={\lambda }_{N-M}\left(P\right)$，则

从而可得

${\stackrel{\dot{}}{V}}_2\le -2c_4{V}_2^{\frac{\alpha +1}{2}}-2c_5{V}_2^{\frac{\beta +1}{2}}-2c_6{V}_2,$ (10)

其中

$c_4=\underset{i\in {\text{Γ}}_f}{\min }\left\{{\rho }_i\right\}{\lambda }^{-\frac{\alpha +1}{2}},c_5={\left(N-M\right)}^{\frac{1-\beta }{2}}\underset{i\in {\text{Γ}}_f}{\min }\left\{k_i\right\}{\lambda }^{-\frac{\beta +1}{2}},c_6=\underset{i\in {\text{Γ}}_f}{\min }\left\{{\xi }_i\right\}{\lambda }^{-1}.$

第二阶段的稳定时间为

$T_2^{\text{*}}=\frac{1}{c_6\left(1-\alpha \right)}\ln \left(1+\frac{c_6}{c_4}\right)+\frac{1}{c_5\left(\beta -1\right)}.$ (11)

因此，系统(3)在协议(4)下可以实现固定时间准包围控制，并且总的调整时间由下式表示

$T^{\text{*}}\le T_1^{\text{*}}+T_2^{\text{*}}.$ (12)

5. 数值模拟

为了验证文中理论结果的有效性，我们考虑图1中一个包含6个智能体的系统，分别标记为 $a_1,a_2,\cdots ,a_6$，其中领导者被标记为 $a_1,a_2,a_3$，智能体 $a_1$ 和智能体 $a_3$ 传播相反的信息，其连接线路由虚线表示。于是邻接矩阵和Laplacian矩阵分别为

$A=\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ 1& 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 1& 0\\ 0& 1& 0& 0& 0& 0\\ 1& 0& 0& 0& 1& 0\end{array}\right]和L=\left[\begin{array}{cccccc}1& -1& 0& 0& 0& 0\\ -1& 2& -1& 0& 0& 0\\ 0& -1& 1& 0& 0& 0\\ 0& 0& -1& 2& -1& 0\\ 0& -1& 0& 0& 1& 0\\ -1& 0& 0& 0& -1& 2\end{array}\right].$

显然，假设4.1是满足的。给定领导者的 ${\delta }_l=diag\left(-2.5,0.4,-2.5\right)$，并选择 $\alpha =0.5,\beta =1.5$ 和 $\rho =k=\xi =diag\left(-0.4,2.5,-0.4,1,1,1\right)$。

内部状态轨迹的时间演变如图2所示，外部状态轨迹的时间演变如图3所示，控制输入轨迹如图4所示，其中领导者的状态和输入用实线表示，跟随者的状态和输入用虚线表示。

Figure 1. The structure of interaction topology

图1. 交互拓扑结构

Figure 2. Inner state trajectories

图2. 内部状态轨迹

Figure 3. Outer state trajectories

图3. 外部状态轨迹

由公式(8)和公式(11)可以估计总的固定时间 $T^{\text{*}}=698.8311$。如图3所示，所有智能体的外部状态在 $t=1.2$ 时达到一致。根据定义3.1，系统(3)可以实现固定时间准包围控制。图2描述了智能体的内部状态。其中，具有相同标度参数 ${\delta }_i$ 的智能体1和智能体3在 $t=1.2$ 时达到一致，具有不同标度参数 ${\delta }_i$ 的智能体2在 $t=0.5$ 时达到稳定状态。显然，内部状态既没有达成集群一致，也没有达成双边一致。在本例中，智能体2的状态是隔离的。事实上，如果所有的标度参数 ${\delta }_i$ 在某些极端情况下是完全不同的，领导者的内部状态就会彼此分离。

Figure 4. Control input trajectories

图4. 控制输入轨迹

6. 结论

本文讨论了存在对抗性节点的多智能体系统的固定时间准包围控制问题。在代数图论和固定时间稳定性定理的基础上，通过给出充分条件，证明了期望的准包围控制可以在有限时间内实现。数值仿真结果表明，在所设计的固定时间控制协议下，多智能体系统可以在较短的时间内实现预期的准包围控制。同时，我们可以发现系统的稳定时间上界 $T^{\text{*}}$ 不受系统初始值的影响，而与控制协议中的参数，拓扑图结构及智能体数量有关。

基金项目

本文得到湖南省自然科学基金项目(2020JJ6003)，湖南省教育厅重点项目(20A425)和湖南省环保科研课题(湘财建二指(2019) 0011号)的支持。

参考文献

NOTES

^*通讯作者。