正项级数的达朗贝尔(D’Alembert)判别法的推广及应用

Generalization on D’Alembert Test of Positive Series and Its Application

摘要: 对正项级数的达朗贝尔判别法进行了推广，并通过实例说明了推广的判别方法的有效性和实用性。

Abstract: This paper gives some generalized results on the basis of value of ratio criterion. Finally, some examples are given to demonstrate the effectiveness and practicability of the generalized method.

1. 引言

正项级数是数项级数中最重要的研究对象。因此，对于正项级数敛散性的研究一直都是人们关注的焦点。达朗贝尔(D’Alembert)判别法(也称为比值判别法或比式判别法)作为正项级数敛散性的一个重要判别法则，因其简单、方便等特点被广泛应用。但该判别方法具有一定的局限性，为此，许多学者对其进行了改进，以期能够判别更多的正项级数的敛散性。文献 [1] 针对正项级数的一般项单调递减的情形，利用柯西定理给出了一种改进的达朗贝尔判别方法，并通过分析指出：该方法比达朗贝尔判别法较为广泛 [1]；文献 [2] 及文献 [3] 对该方法进行了改进；文献 [4] 去掉了一般项单调递减的限制，给出了一种双比值判别法，并说明了双比值判别法强于达朗贝尔判别法；文献 [5] 将双比值判别法推广到了一般的情形；文献 [6] 给出了一种隔项比值判别法，并举例说明了该方法改进了达朗贝尔判别法；文献 [7] 给出了一种更精细的比值判别法。本文在这些文献的基础上，也尝试对达朗贝尔判别法进行推广，使得正项级数的判别方法得到进一步丰富和完善。

达朗贝尔判别法 [8] [9] 设 ${\displaystyle \sum a_n}$ 为正项级数，其中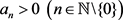，记

$\underset{\_}{d}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{n+1}}{a_n},\bar{d}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{n+1}}{a_n}$ (1)

则

(i) 当 $\bar{d}<1$ 时，该级数收敛；

(ii) 当 $\underset{\_}{d}>1$ 时，该级数发散；

(iii) 当 $\underset{\_}{d}\le 1\le \bar{d}$ 时，该判别法失效。

除特殊说明外，本文所讨论的上、下极限均为有限数。

2. 主要结论及应用

引理1 设 ${\displaystyle \sum a_n}$ 为正项级数，记

$\underset{\_}{p}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{2n-1}}{a_n};\bar{p}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{2n-1}}{a_n};\underset{\_}{q}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{2n}}{a_n};\bar{q}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{2n}}{a_n}.$ (2)

则

(i) 当 $\bar{p}+\bar{q}<1$ 时，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 当 $\underset{\_}{p}+\underset{\_}{q}>1$ 时，级数 ${\displaystyle \sum a_n}$ 发散；

(iii) 当 $\underset{\_}{p}+\underset{\_}{q}\le 1\le \bar{p}+\bar{q}$ 时，该判别法失效。

证 (i)由 $\bar{p}+\bar{q}<1$ 知，存在 ${\epsilon }_0>0$ 使得 $\bar{p}+\bar{q}+{\epsilon }_0<1$。又由

$\underset{n\to \infty }{\bar{\lim }}\frac{a_{2n-1}\text{+}{a}_{2n}}{a_n}\le \bar{p}+\bar{q}$

知，存在 $N_1\in \mathbb{N}$ 使得当 $n>N_1$ 时，有

$a_{2n-1}\text{+}{a}_{2n}<\left(\bar{p}+\bar{q}+{\epsilon }_0\right)a_n$ (3)

由于级数的敛散性与前有限项无关，不妨设(3)式对于所有的自然数 $n>1$ 都有成立，故

$S_n={\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_k}\le S_{2n}={\displaystyle \underset{k=1}{\overset{n}{\sum }}\left(a_{2k-1}+a_{2k}\right)}\le \left(1-\bar{p}-\bar{q}-{\epsilon }_0\right)a_1+a_2+\left(\bar{p}+\bar{q}+{\epsilon }_0\right)S_n$

从而

$S_n\le \frac{\left(1-\bar{p}-\bar{q}-{\epsilon }_0\right)a_1+a_2}{1-\bar{p}-\bar{q}-{\epsilon }_0}$

即 $\left\{S_n\right\}$ 有界，所以级数 ${\displaystyle \sum a_n}$ 收敛。

(ii) 由 $\underset{\_}{p}+\underset{\_}{q}>1$ 知，存在 ${\epsilon }_0>0$ 使得 $\underset{\_}{p}+\underset{\_}{q}-{\epsilon }_0>1$ 成立。又由

$\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{2n-1}\text{+}{a}_{2n}}{a_n}\ge \underset{\_}{p}+\underset{\_}{q}$

知，存在 $N_2\in \mathbb{N}$ 使得当 $n>N_2$ 时，有

$\frac{a_{2n-1}\text{+}{a}_{2n}}{a_n}>\underset{\_}{p}+\underset{\_}{q}-{\epsilon }_0$ (4)

类似于(i)中，不妨设(4)式对于所有的自然数 $n$ 都有成立，故有

$S_{2n}={\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_{2k}}+{\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_{2k-1}}\ge \left(\underset{\_}{p}+\underset{\_}{q}-{\epsilon }_0\right)S_n.$ (5)

若 ${\displaystyle \sum a_n}$ 收敛，则 $\underset{n\to \infty }{\lim }{S}_n$ 存在，设该极限为 $S$。对(5)式两边取极限可得

$S\ge \left(\underset{\_}{p}+\underset{\_}{q}-{\epsilon }_0\right)S>S$

因 $S>0$，这是矛盾的。故 ${\displaystyle \sum a_n}$ 发散。

(iii) 考察级数 ${\displaystyle \underset{n=2}{\overset{\infty }{\sum }}\frac{1}{n{\left(\ln n\right)}^p}}$ 的敛散性 [8] [9]。由于

$\underset{\_}{p}=\bar{p}=\underset{n\to \infty }{\lim }\frac{n{\left(\ln n\right)}^p}{\left(2n-1\right){\left[\ln \left(2n-1\right)\right]}^p}=\frac{1}{2}$

$\underset{\_}{q}=\bar{q}=\underset{n\to \infty }{\lim }\frac{n{\left(\ln n\right)}^p}{2n{\left(\ln 2n\right)}^p}=\frac{1}{2}$，

故 $\underset{\_}{p}+\underset{\_}{q}=\bar{p}+\bar{q}=1$，因此，引理1无法判别其敛散性。但由文献 [8] [9] 知，当 $p>1$ 时，该级数收敛；当 $p\le 1$ 时，该级数发散。

利用引理1可以对达朗贝尔判别法失效的情形做如下改进，使其应用范围更加广泛。

定理1 设 ${\displaystyle \sum a_n}$ 为正项级数， $\underset{\_}{d},\bar{d}$ 如(1)式所示且满足 $0<\underset{\_}{d}\le 1\le \bar{d}$。 $\underset{\_}{p},\bar{p},\underset{\_}{q},\bar{q}$ 如(2)式所示，则

(i) 当 $\bar{q}<\frac{\underset{\_}{d}}{1+\underset{\_}{d}}$ 时，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 当 $\underset{\_}{q}>\frac{\bar{d}}{1+\bar{d}}$ 时，级数 ${\displaystyle \sum a_n}$ 发散；

(iii) 当 $\underset{\_}{q}\le \frac{\bar{d}}{1+\bar{d}}$ 且 $\bar{q}\ge \frac{\underset{\_}{d}}{1+\underset{\_}{d}}$ 时，该判别法失效。

证 (i) 因为

$\bar{p}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{2n-1}}{a_n}\le \underset{n\to \infty }{\bar{\lim }}\frac{a_{2n-1}}{a_{2n}}\cdot \underset{n\to \infty }{\bar{\lim }}\frac{a_{2n}}{a_n}=\frac{1}{\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{2n}}{a_{2n-1}}}\cdot \underset{n\to \infty }{\bar{\lim }}\frac{a_{2n}}{a_n}\le \frac{\bar{q}}{\underset{\_}{d}}<\frac{1}{1+\underset{\_}{d}}$

故 $\bar{p}+\bar{q}<1$，由引理1(i)知，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 因为

$\underset{\_}{p}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{2n-1}}{a_n}\ge \underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{2n-1}}{a_{2n}}\cdot \underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{2n}}{a_n}=\frac{1}{\underset{n\to \infty }{\bar{\lim }}\frac{a_{2n}}{a_{2n-1}}}\cdot \underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{2n}}{a_n}\ge \frac{\underset{\_}{q}}{\bar{d}}>\frac{1}{1+\bar{d}}$

故 $\underset{\_}{p}+\underset{\_}{q}>1$，由引理1(ii)知，级数 ${\displaystyle \sum a_n}$ 发散。

(iii) 考察级数 ${\displaystyle \underset{n=3}{\overset{\infty }{\sum }}\frac{1}{n\ln n{\left(\ln \ln n\right)}^p}}$ 的敛散性。由于

$\underset{\_}{d}=\bar{d}=\underset{n\to \infty }{\lim }\frac{n\ln n{\left(\ln \ln n\right)}^p}{\left(n+1\right)\ln \left(n+1\right){\left[\ln \ln \left(n+1\right)\right]}^p}=1$

$\underset{\_}{q}=\bar{q}=\underset{n\to \infty }{\lim }\frac{n\ln n{\left(\ln \ln n\right)}^p}{2n\ln 2n{\left(\ln \ln 2n\right)}^p}=\frac{1}{2}$

因此， $\underset{\_}{q}=\frac{\bar{d}}{1+\bar{d}},\bar{q}=\frac{\underset{\_}{d}}{1+\underset{\_}{d}}$，故定理1无法判别其敛散性。但由文献 [2] 知，当 $p>1$ 时，该级数收敛；当 $p\le 1$

时，该级数发散。

类似定理1，可得

定理2 设 ${\displaystyle \sum a_n}$ 为正项级数， $\underset{\_}{d},\bar{d}$ 如(1)式所示且满足 $0<\underset{\_}{d}\le 1\le \bar{d}$。 $\underset{\_}{p},\bar{p},\underset{\_}{q},\bar{q}$ 如(2)式所示，则

(i) 当 $\bar{p}<\frac{1}{1+\bar{d}}$ 时，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 当 $\underset{\_}{p}>\frac{1}{1+\underset{\_}{d}}$ 时，级数 ${\displaystyle \sum a_n}$ 发散；

(iii) 当 $\underset{\_}{p}\le \frac{1}{1+\underset{\_}{d}}$ 且 $\bar{p}\ge \frac{1}{1+\bar{d}}$ 时，该判别法失效。

定理2的证明完全类似于定理1，在此省略其证明过程。下面讨论引例1的推广，给出如下的引理2.

引理2 设 ${\displaystyle \sum a_n}$ 为正项级数，记

$\underset{\_}{r}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n-1}}{a_n},\bar{r}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{3n-1}}{a_n};\underset{\_}{s}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n}}{a_n},\bar{s}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{3n}}{a_n};\underset{\_}{t}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n+1}}{a_n},\bar{t}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{3n+1}}{a_n}$ (6)

则

(i) 当 $\bar{r}+\bar{s}+\bar{t}<1$ 时，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 当 $\underset{\_}{r}+\underset{\_}{s}+\underset{\_}{t}>1$ 时，级数 ${\displaystyle \sum a_n}$ 发散；

(iii) 当 $\underset{\_}{r}+\underset{\_}{s}+\underset{\_}{t}\le 1\le \bar{r}+\bar{s}+\bar{t}$ 时，该判别法失效。

证 (i) 类似于(3)式，存在 ${\epsilon }_0>0$ 使得 $\left(\bar{r}+\bar{s}+\bar{t}+{\epsilon }_0\right)<1$ 且对于所有的自然数 $n\ge 1$ 都有

$a_{3n-1}\text{+}{a}_{3n}+a_{3n+1}<\left(\bar{r}+\bar{s}+\bar{t}+{\epsilon }_0\right)a_n$

于是

$S_n={\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_k}\le S_{3n}=a_1+{\displaystyle \underset{k=1}{\overset{n}{\sum }}\left(a_{3k-1}+a_{3k}+a_{3k+1}\right)}\le a_1+\left(\bar{r}+\bar{s}+\bar{t}+{\epsilon }_0\right)S_n$

从而

$S_n\le \frac{a_1}{1-\bar{r}-\bar{s}-\bar{t}-{\epsilon }_0}$

故此时级数收敛。

(ii) 类似于(4)式，存在 ${\epsilon }_0>0$ 使得 $\underset{\_}{r}+\underset{\_}{s}+\underset{\_}{t}-{\epsilon }_0>1$ 且对于所有的自然数 $n$ 都有

$a_{3n-1}\text{+}{a}_{3n}+a_{3n+1}>\left(\underset{\_}{r}+\underset{\_}{s}+\underset{\_}{t}-{\epsilon }_0\right)a_n$

于是

$S_{3n}=a_1+{\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_{3k-1}}+{\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_{3k}}+{\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_{3k+1}}\ge \left(\underset{\_}{r}+\underset{\_}{s}+\underset{\_}{t}-{\epsilon }_0\right)S_n+\left(1-\underset{\_}{r}-\underset{\_}{s}-\underset{\_}{t}+{\epsilon }_0\right)a_1$

若 ${\displaystyle \sum a_n}$ 收敛，则 $\underset{n\to \infty }{\lim }{S}_n$ 存在，设该极限为 $S$。对上式两边取极限可得

$S\ge \left(\underset{\_}{r}+\underset{\_}{s}+\underset{\_}{t}-{\epsilon }_0\right)S+\left(1-\underset{\_}{r}-\underset{\_}{s}-\underset{\_}{t}+{\epsilon }_0\right)a_1>S+\left(1-\underset{\_}{r}-\underset{\_}{s}-\underset{\_}{t}+{\epsilon }_0\right)a_1$

因 $1-\underset{\_}{r}-\underset{\_}{s}-\underset{\_}{t}+{\epsilon }_0<0$，故得矛盾。因此，级数 ${\displaystyle \sum a_n}$ 发散。

(iii) 考察级数 ${\displaystyle \underset{n=30}{\overset{\infty }{\sum }}\frac{1}{n\cdot \ln n\cdot \ln \ln n\cdot {\left(\ln \ln \ln n\right)}^p}}$ 的敛散性。由于

$\underset{\_}{r}=\bar{r}=\underset{n\to \infty }{\lim }\frac{n\cdot \ln n\cdot \ln \ln n\cdot {\left(\ln \ln \ln n\right)}^p}{\left(3n-1\right)\cdot \ln \left(3n-1\right)\cdot \ln \ln \left(3n-1\right)\cdot {\left[\ln \ln \ln \left(3n-1\right)\right]}^p}=\frac{1}{3}$

$\underset{\_}{s}=\bar{s}=\underset{n\to \infty }{\lim }\frac{n\cdot \ln n\cdot \ln \ln n\cdot {\left(\ln \ln \ln n\right)}^p}{3n\cdot \ln 3n\cdot \ln \ln 3n\cdot {\left(\ln \ln \ln 3n\right)}^p}=\frac{1}{3}$

$\underset{\_}{t}=\bar{t}=\underset{n\to \infty }{\lim }\frac{n\cdot \ln n\cdot \ln \ln n\cdot {\left(\ln \ln \ln n\right)}^p}{\left(3n+1\right)\cdot \ln \left(3n+1\right)\cdot \ln \ln \left(3n+1\right)\cdot {\left[\ln \ln \ln \left(3n+1\right)\right]}^p}=\frac{1}{3}$

因此 $\underset{\_}{r}+\underset{\_}{s}+\underset{\_}{t}=1=\bar{r}+\bar{s}+\bar{t}$，故引理2无法判别其敛散性。但由文献 [3] 知，当 $p>1$ 时，该级数收敛；当 $p\le 1$ 时，该级数发散。

由引理2可得如下定理3~5，证明均类似于定理1，在此只给出定理3的证明，其余证明省略。

定理3设 ${\displaystyle \sum a_n}$ 为正项级数， $\underset{\_}{d},\bar{d}$ 如(1)式所示且满足 $0<\underset{\_}{d}\le 1\le \bar{d}$。 $\underset{\_}{r},\underset{\_}{s},\underset{\_}{t}$ 及 $\bar{r},\bar{s},\bar{t}$ 如(6)式所示，则

(i) 当 $\bar{s}<\frac{\underset{\_}{d}}{1+\underset{\_}{d}+\underset{\_}{d}\bar{d}}$ 时，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 当 $\underset{\_}{s}>\frac{\bar{d}}{1+\bar{d}+\underset{\_}{d}\bar{d}}$ 时，级数 ${\displaystyle \sum a_n}$ 发散；

(iii) 当 $\underset{\_}{s}\le \frac{\bar{d}}{1+\bar{d}+\underset{\_}{d}\bar{d}}$ 且 $\bar{s}\ge \frac{\underset{\_}{d}}{1+\underset{\_}{d}+\underset{\_}{d}\bar{d}}$ 时，该判别法失效。

证 (i) 由于

$\bar{t}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{3n+1}}{a_n}\le \underset{n\to \infty }{\bar{\lim }}\frac{a_{3n+1}}{a_{3n}}\cdot \underset{n\to \infty }{\bar{\lim }}\frac{a_{3n}}{a_n}<\frac{\underset{\_}{d}\bar{d}}{1+\underset{\_}{d}+\underset{\_}{d}\bar{d}}$

$\bar{r}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{3n-1}}{a_n}\le \underset{n\to \infty }{\bar{\lim }}\frac{a_{3n-1}}{a_{3n}}\cdot \underset{n\to \infty }{\bar{\lim }}\frac{a_{3n}}{a_n}=\frac{1}{\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n}}{a_{3n-1}}}\cdot \underset{n\to \infty }{\bar{\lim }}\frac{a_{3n}}{a_n}<\frac{1}{1+\underset{\_}{d}+\underset{\_}{d}\bar{d}}$

因此 $\bar{r}+\bar{s}+\bar{t}<1$，由引理2(i)知级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 由于

$\underset{\_}{t}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n+1}}{a_n}\ge \underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n+1}}{a_{3n}}\cdot \underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n}}{a_n}>\frac{\underset{\_}{d}\bar{d}}{1+\bar{d}+\underset{\_}{d}\bar{d}}$

$\underset{\_}{r}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n-1}}{a_n}\ge \underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n-1}}{a_{3n}}\cdot \underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n}}{a_n}=\frac{1}{\underset{n\to \infty }{\bar{\lim }}\frac{a_{3n}}{a_{3n-1}}}\cdot \underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{3n}}{a_n}>\frac{1}{1+\bar{d}+\underset{\_}{d}\bar{d}}$

因此 $\underset{\_}{r}+\underset{\_}{s}+\underset{\_}{t}>1$，再由引理2(ii)知级数 ${\displaystyle \sum a_n}$ 发散。

(iii) 考察级数 ${\displaystyle \underset{n=30}{\overset{\infty }{\sum }}\frac{1}{n\cdot {\left(\ln n\right)}^p\cdot {\left(\ln \ln n\right)}^q\cdot {\left(\ln \ln \ln n\right)}^r}}$ 的敛散性 [3]。由于

$\underset{\_}{d}=\bar{d}=\underset{n\to \infty }{\lim }\frac{n\cdot {\left(\ln n\right)}^p\cdot {\left(\ln \ln n\right)}^q\cdot {\left(\ln \ln \ln n\right)}^r}{\left(n+1\right)\cdot {\left[\ln \left(n+1\right)\right]}^p\cdot {\left[\ln \ln \left(n+1\right)\right]}^q\cdot {\left[\ln \ln \ln \left(n+1\right)\right]}^r}=1$

$\underset{\_}{s}=\bar{s}=\underset{n\to \infty }{\lim }\frac{n\cdot {\left(\ln n\right)}^p\cdot {\left(\ln \ln n\right)}^q\cdot {\left(\ln \ln \ln n\right)}^r}{3n\cdot {\left(\ln 3n\right)}^p\cdot {\left(\ln \ln 3n\right)}^q\cdot {\left(\ln \ln \ln 3n\right)}^r}=\frac{1}{3}$

因此，

$\underset{\_}{s}=\frac{\bar{d}}{1+\bar{d}+\underset{\_}{d}\bar{d}},\bar{s}=\frac{\underset{\_}{d}}{1+\underset{\_}{d}+\underset{\_}{d}\bar{d}}$，

故定理3无法判别其敛散性。但由文献 [3] 知，当 $p=1,q=1,r>1$ 或者 $p=1,q>1,r\in ℝ$ 或者 $p>1,q\in ℝ,r\in ℝ$ 时，该级数收敛；其余情形该级数发散。

定理4设 ${\displaystyle \sum a_n}$ 为正项级数， $\underset{\_}{d},\bar{d}$ 如(1)式所示且满足 $0<\underset{\_}{d}\le 1\le \bar{d}$。 $\underset{\_}{r},\underset{\_}{s},\underset{\_}{t}$ 及 $\bar{r},\bar{s},\bar{t}$ 如(6)式所示，则

(i) 当 $\bar{r}<\frac{1}{1+\bar{d}+{\bar{d}}^2}$ 时，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 当 $\underset{\_}{r}>\frac{1}{1+\underset{\_}{d}+{\underset{\_}{d}}^2}$ 时，级数 ${\displaystyle \sum a_n}$ 发散；

(iii) 当 $\underset{\_}{r}\le \frac{1}{1+\underset{\_}{d}+{\underset{\_}{d}}^2}$ 且 $\bar{r}\ge \frac{1}{1+\bar{d}+{\bar{d}}^2}$ 时，该判别法失效。

定理5设 ${\displaystyle \sum a_n}$ 为正项级数， $\underset{\_}{d},\bar{d}$ 如(1)式所示且满足 $0<\underset{\_}{d}\le 1\le \bar{d}$。 $\underset{\_}{r},\underset{\_}{s},\underset{\_}{t}$ 及 $\bar{r},\bar{s},\bar{t}$ 如(6)式所示，则

(i) 当 $\bar{t}<\frac{{\underset{\_}{d}}^2}{1+\underset{\_}{d}+{\underset{\_}{d}}^2}$ 时，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 当 $\underset{\_}{t}>\frac{{\bar{d}}^2}{1+\bar{d}+{\bar{d}}^2}$ 时，级数 ${\displaystyle \sum a_n}$ 发散；

(iii) 当 $\underset{\_}{t}\le \frac{{\bar{d}}^2}{1+\bar{d}+{\bar{d}}^2}$ 且 $\bar{t}\ge \frac{{\underset{\_}{d}}^2}{1+\underset{\_}{d}+{\underset{\_}{d}}^2}$ 时，该判别法失效。

由前述的证明可以看出引理1和引理2可以进一步推广到更一般情形，且可以得出类似定理1~5的结论，但因篇幅所限在此不再列出更多的结论。下面应用本文的结论讨论一些级数的敛散性。

例1判断级数 ${\displaystyle \underset{n=1}{\overset{\infty }{\sum }}\frac{n^n}{n!{\left(1+\frac{1}{n}\right)}^{n^2}}}$ 的敛散性。

解 由于

$\underset{\_}{d}=\bar{d}=\underset{n\to \infty }{\lim }\frac{a_{n+1}}{a_n}=\underset{n\to \infty }{\lim }\frac{{\left(n+1\right)}^{n+1}}{\left(n+1\right)!{\left(1+\frac{1}{n+1}\right)}^{{(n+1)}^2}}\cdot \frac{n^n}{n!{\left(1+\frac{1}{n}\right)}^{n^2}}=1$

此时达朗贝尔判别法失效。利用Stirling公式 [9] 可得

$\underset{n\to \infty }{\lim }\frac{a_{2n}}{a_n}=\underset{n\to \infty }{\lim }{2}^{2n}{n}^n\cdot \frac{{\left(1+\frac{1}{n}\right)}^{n^2}}{{\left(1+\frac{1}{2n}\right)}^{{(2n)}^2}}\cdot \frac{\sqrt{2\pi n}{\left(\frac{n}{e}\right)}^n{e}^{\frac{{\theta }_n}{12n}}}{\sqrt{4\pi n}{\left(\frac{2n}{e}\right)}^{2n}{e}^{\frac{{\theta }_{2n}}{24n}}}=\frac{1}{\sqrt{2}}\underset{n\to \infty }{\lim }\frac{e^n{\left(1+\frac{1}{n}\right)}^{n^2}}{{\left(1+\frac{1}{2n}\right)}^{{(2n)}^2}}=\frac{\sqrt{2}}{2}$

故 $\underset{\_}{q}=\bar{q}=\frac{\sqrt{2}}{2}>\frac{1}{2}=\frac{1}{1+\bar{d}}$，由定理1知该级数发散。

例2 [8] 讨论级数

$1+b+bc+b^{2}c+b^2{c}^2+\cdots +b^{n-1}{c}^n+b^n{c}^n+\cdots$ (7)

数的敛散性，其中 $0<b<1<c$.

解 由于

$\underset{\_}{d}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{n+1}}{a_n}=b<1,\bar{d}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{n+1}}{a_n}=c>1$

因此，达朗贝尔判别法失效。

当 $bc<1$ 时，由于

$\underset{\_}{s}=\bar{s}=\underset{n\to \infty }{\lim }\frac{a_{3n}}{a_n}=\underset{n\to \infty }{\lim }{\left(bc\right)}^n=0$

且 $\underset{\_}{r}=\bar{r}=\underset{\_}{t}=\bar{t}=0.$ 故由引理2或者定理3~5均可判别该级数收敛。

当 $bc=1$ 或者 $bc>1$ 时，由级数(7)的形式可以判断出此时级数是发散的。

众所周知，拉贝判别法也是正项级数敛散性判别中常用的一种方法，并且拉贝判别法判别范围较达朗贝尔判别法更广泛 [8]。

拉贝判别法 [10] 设 ${\displaystyle \sum a_n}$ 为正项级数，记

$\underset{\_}{R}=\underset{n\to \infty }{\underset{\_}{\lim }}n\left(\frac{a_n}{a_{n+1}}-1\right),\bar{R}=\underset{n\to \infty }{\bar{\lim }}n\left(\frac{a_n}{a_{n+1}}-1\right)$

则

(i) 当 $\underset{\_}{R}>1$ 时，级数 ${\displaystyle \sum a_n}$ 收敛；

(ii) 当 $\bar{R}<1$ 时，级数 ${\displaystyle \sum a_n}$ 发散；

(iii) 当 $\underset{\_}{R}\le 1\le \bar{R}$ 时，该判别法失效。

特别需要指出的是：本文引理1给出的判别方法要强于拉贝判别法。因为，若 $\underset{\_}{R}>1$，则可取 $1<s_1<s_2<\underset{\_}{R}$，当 $n$ 充分大时，有

$\frac{a_n}{a_{n+1}}>1+\frac{s_2}{n}>{\left(1+\frac{1}{n}\right)}^{s_1}$

故

$\frac{a_{n+1}}{a_n}<{\left(\frac{n}{n+1}\right)}^{s_1}$

从而

$\frac{a_{2n}}{a_n}=\frac{a_{2n}}{a_{2n-1}}\cdot \frac{a_{2n-1}}{a_{2n-2}}\cdots \frac{a_{n+1}}{a_n}<{\left(\frac{2n-1}{2n}\cdot \frac{2n-2}{2n-1}\cdots \frac{n}{n+1}\right)}^{s_1}=\frac{1}{2^{s_1}}$

故

$\bar{q}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{2n}}{a_n}\le \frac{1}{2^{s_1}}$

同理可证

$\bar{p}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{2n-1}}{a_n}\le \frac{1}{2^{s_1}}$

故有

$\bar{p}+\bar{q}\le \frac{2}{2^{s_1}}<1$.

类似可证当 $\bar{R}<1$ 时，有 $\underset{\_}{p}+\underset{\_}{q}>1$。由此可知：能够用拉贝判别法确定敛散性的级数均可用引理1确定。反之则不能，如下例。

例3 判断级数 ${\displaystyle \underset{n=1}{\overset{\infty }{\sum }}\frac{1}{2^{n+{(-1)}^{\frac{n(n+1)}{2}}}}}$ 的敛散性。

解 由

$\underset{\_}{d}=\underset{n\to \infty }{\underset{\_}{\lim }}\frac{a_{n+1}}{a_n}=\frac{1}{2^3}<1<\bar{d}=\underset{n\to \infty }{\bar{\lim }}\frac{a_{n+1}}{a_n}=2$，

故达朗贝尔判别法失效。又

$\underset{\_}{R}=\underset{n\to \infty }{\underset{\_}{\lim }}n\left(\frac{a_n}{a_{n+1}}-1\right)=-\infty ,\bar{R}=\underset{n\to \infty }{\bar{\lim }}n\left(\frac{a_n}{a_{n+1}}-1\right)=+\infty$

故拉贝判别法也失效。但易得 $\underset{\_}{p}=\bar{p}=0$， $\underset{\_}{q}=\bar{q}=0$，利用引理1或者定理1或者定理2均可判别该级数收敛。

基金项目

本文受到广东石油化工学院科研基金人才引进项目(2019rc101)、国家自然科学资金青年资金项目(11701114)资助。

NOTES

^*通讯作者。