1. 引言
马拉松是一个历史悠久的体育项目,在国际上普遍分全程马拉松(Full Marathon)、半程马拉松(Half Marathon)和四分马拉松(Quarter Marathon)三种,一般提及马拉松即指全程马拉松。第一次马拉松赛出现在1896年举行的雅典奥林匹克运动会上,路线是在马拉松至雅典之间,全程40.200 km。在1908年伦敦奥运会上, 马拉松的长度改为42.195 km,但将这个距离正式作为马拉松赛事标准长度却是在1924年 [1]。随着波士顿、纽约、柏林、芝加哥等城市成功举办马拉松赛,城市马拉松开始进入大众视野 [2]。
马拉松同样也是一个城市最好的“名片”,它能够把大众视野带入到城市的美景中,对城市文化进行宣传的同时带动当地的经济发展 [3] [4] [5] [6]。据兰州市统计局官网数据显示,2011年兰州国际马拉松赛事创办后的旅游总收入较2010年增幅57.96% [7]。
世界田径组织的任务是在世界上开展田径运动、制定国际比赛的章程和规则、解决在田径运动中出现的有争议的问题以及与奥运会组委会合作举办田径比赛等。全程马拉松必须要满足该组织对赛道的各项规则与要求。根据世界田径规定,马拉松赛道的要求如下 [8]:1) 起点和终点之间的直线距离不得超过比赛竞赛总距离的50%,起点和终点可以在运动场内进行;2) 起点和终点之间的总高程变化不得超过1:1000,即每公里不超过1米;3) 比赛应在人造道路上进行。当交通等情况无法满足要求时,可安排在路旁的自行车道或人行道上,但不得位于软土地上,例如草地边缘等;4) 马拉松的标准距离为42.195 km。在满足要求的基础上,为了更能体现城市风貌,马拉松路线选择尤为重要。现在成熟的马拉松赛事的路线已经很少做出改变,新的马拉松路线一般由主办方根据地形图以及城市特色文化地标进行手动规划路线,最后利用装有琼斯计数器的校准自行车进行测量赛道。选择过程比较繁重,需要耗费大量的资源才能满足世界田联对马拉松的要求。
针对路线规划问题,现在常用的代表性算法有蚁群算法、粒子群优化算法、迪杰斯特拉(Dijkstra)算法、A*算法等,其中A*算法是经典启发式搜索算法之一。国内外学者也提出很多改进策略。王小红、叶涛 [9] 将传统的8邻域搜索拓展到24邻域,提高了路径搜索的自由度,并与动态窗口法结合,提高了路径的平滑度与安全性,缺点在于在大规模地图中,会由于计算量过大,导致机器人实时性能低下,效果不如传统算法。曹莹等人 [10] 将障碍物安全距离引入启发式函数,从而降低智能小车碰撞威胁,但是该算法在复杂地图中规划时间不能保证。倪昌浩,邹海 [11] 在无人机航迹规划中引入危险因子并对节点附近搜索区域进行探测,提高算法提前预知风险的能力。
针对上述文献中的改进A*算法会因为地图所提供的信息过于精确,而导致算法计算成本大、时间较长的问题,本文利用邻接表和邻接矩阵反应地图信息,在简化地图的同时提供了地图道路路口的基本信息,大大减小了算法生成路径时的计算成本,并将改进的A*算法与马拉松赛事相结合,提供一种马拉松路线的初步选择方法,使得路线最大程度地反映举办城市的特色。
2. 研究方法
2.1. 研究思路
本文从测绘技术的角度出发,将马拉松选线的内容和要求转化为实现初步路线的所需条件(如表1)。本文利用缓冲区和高精度数字高程模型(DEM)分别保证起终点间的直线距离和总高程满足要求,采用细化道路网的方法筛选道路之后,再利用改进的A*算法满足地标要求的同时生成完整路线,整体流程图如图1。
2.2. A*算法及改进
A*算法的估价函数可以表示为:
(1)
其中:
为估价函数,表示从起始点到目标点的估计代价;
指在状态空间中从初始
节点到节点n的实际代价;
是节点n到目标节点最佳路径的估计代价 [12]。
在A*算法中,使用了两个状态表,分别称为Open表和Closed表。开始时,Closed表为空(Open表仅包括起始节点)。每次迭代中,A*算法将Open表中具有最小代价的节点进行检查,如果这个节点不是目标节点,那么考虑该节点的其它相邻节点。
本文旨在改进A*算法,使得该算法可以智能匹配地标,规划出一条路过地标的路线。具体的改进如下:
1) 根据地标的经纬度计算得到地标的空间直角坐标,获取曼哈顿距离并利用最近邻算法 [13] 进行编程,实现智能匹配到离地标最近的路口交点。在二维平面两点
与
的曼哈顿距离为:
(2)
2) 根据起终点和与路口交点的曼哈顿距离按顺序拆分路径,然后根据此顺序分别利用A*算法生成分段路线。最后将所有分段路线连接,生成完整路线。改进A*算法流程图如图2所示。

Figure 2. Flow chart of improved A* algorithm
图2. 改进A*算法流程图
3. 数据处理及分析
1) 筛选赛道道路
城市马拉松的赛道要求宽度尽量在9 m以上,且最窄处不能低于6 m。按照国家道路标准,城市道路分为四级,其中一级、二级、三级道路符合宽度要求。利用ArcMap将路网矢量数据按照不同属性进行筛选,再编辑脚本代码细化道路网。然后利用高精度数字高程模型进行叠加分析,筛选符合坡度变化的道路,最终得到符合要求的道路网(图3)。
2) 储存交点信息
利用ArcMap在道路网上建立拓扑关系,打断道路并在相交处生成点要素。编写程序遍历交点,通过邻接矩阵存储交点之间的关系,如图4、图5所示。
(3)
其中,V表示顶点集合,E表示边集合 [14]。

Figure 4. Schematic diagram of point relationship
图4. 点关系示意图
3) 选择起终点
起终点相同时,根据举办城市的地形图,选择流通性较好的大型广场或体育场,选择的广场必须保证参赛人员在正常情况下不会拥挤。按照正常情况下,成年人在正常情况下站立需要0.2~0.4 m2的面积,所以该场地必须可以保证人均至少有0.4 m2面积。比如,北京马拉松的起点天安门的面积大约在440,000 m2,在参赛人数最多的一届也可以保证人均拥有2.75 m2左右的面积。
起终点不同时,利用举办地区的地形图,获得起点的具体坐标
,根据空间目标
设置缓冲区来满足起点终点的直线距离小于21.0975公里的要求:
(4)
公式(4)中,R为邻域半径,即缓冲距,设为21.0975公里;d一般指最小欧氏距离,但也可以是其他定义的距离;
为
的缓冲距为R的缓冲区。在到
距离d小于或等于R的所有点的集合中选择终点 [15]。
4) 储存地标信息
了解当地文化,筛选最能反映该地区人文景色的地标。获取该地标的经纬度并进行坐标转换,得到空间直角坐标系下的横坐标(X)和纵坐标(Y)。转化公式为:
(5)
其中,B为纬度、L为精度;N为椭圆曲率半径、H为海拔。
4. 实验与结果
在OpenStreetMap上下载北京道路网数据,在ArcMap中将道路网根据属性表中的种类进行筛选并利用字段计算器编写脚本进行细化道路网。利用拓扑工具,将筛选后的路网数据建立拓扑关系、打断道路网、获得交点信息(图6)。通过编程遍历道路网数据的交点信息,生成邻接矩阵和邻接表。
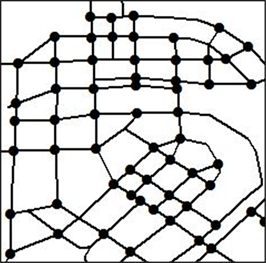
Figure 6. Part of Beijing intersection network
图6. 部分北京路口关系网
按照北京马拉松的传统,将起点设置为天安门广场,终点设置为国家体育馆和水立方之间的广场。选择国家大剧院、民族文化馆、军事博物馆、玉渊潭公园、中央电视塔、昆明湖、稻香园桥、水立方、奥林匹克森林公园和国家体育场作为北京的地方性标志性地点。获取这10个地标的经纬度,通过坐标转化公式得到空间直角坐标,利用改进的A*算法得到路线。并将此路线与利用传统A*算法得到的路线相比较,如图7所示。传统方法只获得了一条在起终点间最短的路线,并没有路过地标,证明了本文改进的A*算法对于马拉松路线规划的优势。
将生成的路线图与2019年北京马拉松路线图相比较(如图8),得到结论如下:1) 二者走向一致;2) 二者经过地标一致;3) 二者在水立方之后的路线发生巨大差异,而且可以看出2019年北京马拉松比赛路线明显长于本文算法生成的路线图。
前两条结论验证了本文改进的A*算法可以在马拉松路线选择上进行应用。而二者在水立方之后的路线发生巨大差异的原因可能在于:1) A*算法是一种求解最短路径搜索方法,在节点的曼哈顿距离接近时,可能会出现规划路线的差异;2) A*算法在相同的起终点上,生成的是一条最短路径,不可能得到反复路径。在进行两个原因的对比实验后,发现本文生成的路线差异符合第二个原因。
5. 结语
本文针对传统A*算法在规划复杂地图路线时会因为地图点信息过多,导致的计算成本大、效率低的问题,将传统算法改进,使得算法不再遍历图中的每一个点,而是读取储存着点间关系的邻接表和邻接矩阵。通过对比,发现改进后的A*算法相较于之前计算成本小。并且本文应用改进后的A*算法进行马拉松路线规划,可以得到一条经过地标的路线。此方法有效地简化了马拉松选线工作中的繁琐步骤,使马拉松路线的选线更加高效、直观,为马拉松的路线选取提供思路。针对本文中路线的对比结果,还需再将程序完善,做进一步研究。
参考文献