简单波和二维非线性波动系统的特征分解

Simple Waves and Characteristic Decompositions of the Two-Dimensional Nonlinear Wave System

摘要: 本文考虑具有广义Chaplygin气体的二维非线性波动系统，对可压缩欧拉系统进行简化，得到了自相似平面上压力变量和倾斜角变量沿着特征线的简单波和一些特征分解，这些结果是Courant和Friedrichs专著中关于可约方程的著名定理的推广。

Abstract: In this paper, we consider a two-dimensional nonlinear wave system with generalized Chaplygin gas which is simplified model of the compressible Euler system and get simple waves and some characteristic decompositions for the pressure variable and inclination angle variables along the characteristic curves in the self-similar plane. These results are generalization of the well-known theorem on reducible equations in Courant and Friedrichs’s monograph.

1. 引言

黎曼不变量的存在在双曲守恒律系统解的构造中起着基础性的作用，例如波动方程中D’Alembert公式的构造，以及奇点的发展证明 [1]。对于二维定常等熵无旋欧拉方程组，由于黎曼不变量的存在，任何与定常状态相邻的解都是一个简单波 [2]。黎曼不变量帮助我们得出任何与常状态相邻的双曲状态的解都是简单波的结论，然而，由于黎曼不变量对于n > 2可能一般不存在，这种方法有局限性。

Dai和Zhang [3] 首次为压力梯度系统揭示了特征分解是作为构建全局平滑解斑块的强大工具。Li、Zhang和Zheng [4] 使用特征分解技术研究了准线性双曲系统，证明了一个非常重要的结果，绝热欧拉系统在自相似平面上相邻的一个恒定状态是一个简单波，其中物理变量 $\left(u,v,c,p,\rho \right)$ 沿着波的直线特征族是恒定的。Hu和Sheng [5] 建立了广义2阶拟线性严格双曲方程组特征分解存在的一个充分条件。通过使用特征分解技术，我们不仅发现了黎曼变量，而且还发现了在一些双曲系统中所谓的Riemann变量。因此特征分解方法是处理拟线性双曲系统问题的一种有效方法 [4] [6] [7] [8] [9]。

本文考虑二维非线性波动系统

$\{\begin{array}{l}{\rho }_t+{\left(\rho u\right)}_x+{\left(\rho v\right)}_y=0,\\ {\left(\rho u\right)}_t+p_x=0,\\ {\left(\rho v\right)}_t+p_y=0,\end{array}$ (1.1)

其中 $\rho$ 为密度， $\left(u,v\right)$ 为速度，状态方程 $p=p\left(\rho \right)$ 是 $\rho$ 的赋值函数，系统(1.1)是通过忽略气体动力学中二维可压缩Euler方程速度 $\left(u,v\right)$ 的二次项而得到的，Čanić、Keyfitz、Kim [10] 分别推导了非线性波动系统和可压缩气体动力学绝热方程的混合系统，并证明了所产生的混合系统具有复杂的非线性相关性。Hu和Wang [11] 提出了压力的特征分解，并利用分解建立先验估计，构造了带有Chaplygin气体的系统(1.1)的半双曲片的全局解。本文我们推导了压力变量和角变量的一些有趣的特征分解。

在本文中，我们感兴趣的是修正的Chaplygin气体

$p=A\rho -\frac{B}{{\rho }^{\alpha }},$ (1.2)

其中参数 $\alpha >0,A>0,B>0$，它是用来描述当前宇宙的加速膨胀 [12]。注意到当 $A=0,\alpha =1$ 时，(1.2)由Chaplygin [13] 和Tsien [14] 引入，作为空气动力学中计算飞机机翼升力的合适数学近似。另一方面，对于 $A=0,0<\alpha <1$，该模型给出了从初始尘埃类物质到渐进宇宙常数的宇宙学演化。这一广义模型以前已经被研究 [15]。

为了进一步研究系统(1.1)的内在特征，我们的主要系统是(1.1)在自相似变量 $\left(\xi ,\eta \right)=\left(x/t,y/t\right)$ 下的系统

$\{\begin{array}{l}\xi {\rho }_{\xi }+\eta {\rho }_{\eta }-{\left(\rho u\right)}_{\xi }-{\left(\rho v\right)}_{\eta }=0,\\ \xi {\left(\rho u\right)}_{\xi }+\eta {\left(\rho u\right)}_{\eta }-p_{\xi }=0,\\ \xi {\left(\rho v\right)}_{\xi }+\eta {\left(\rho v\right)}_{\eta }-p_{\eta }=0.\end{array}$ (1.3)

我们写(1.3)为矩阵形式

$L{W}_{\xi }+Q{W}_{\eta }=0,$ (1.4)

其中

$\begin{array}{l}a\left(p\right)=\frac{1}{{\rho }^{\prime }\left(p\right)}=A+B\alpha {\rho }^{-\alpha -1},W={\left(p,u,v\right)}^{\prime },\\ L=\left(\begin{array}{ccc}u-\xi & a\rho & 0\\ \xi u-a& a\rho \xi & 0\\ \xi v& 0& a\rho \xi \end{array}\right)，Q=\left(\begin{array}{ccc}v-\eta & 0& a\rho \\ \eta u& a\rho \eta & 0\\ \eta v-a& 0& a\rho \eta \end{array}\right).\end{array}$

通过简单计算，我们得到(1.4)的特征方程

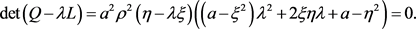(1.5)

并且特征值为

${\lambda }_0=\frac{\eta }{\xi },{\lambda }_{\pm }=\frac{\xi \eta \pm \sqrt{a\left({\xi }^2+{\eta }^2-a\right)}}{{\xi }^2-a}.$ (1.6)

系统(1.4)在 ${\xi }^2+{\eta }^2=a$ 处改变了类型，且当 ${\xi }^2+{\eta }^2>a$ 时为双曲型。我们注意到系统(1.1)的特征值与 $\left(u,v\right)$ 无关，这意味着(1.1)可以转化为一个仅关于p的偏微分方程。

2. 预备知识

我们首先将p从 $\left(\rho u\right)$ 和 $\left(\rho v\right)$ 中解耦得到一个二阶拟线性方程

$\left(a\left(p\right)-{\xi }^2\right)p_{\xi \xi }-2\xi \eta p_{\xi \eta }+\left(a\left(p\right)-{\eta }^2\right)p_{\eta \eta }+b\left(p\right){\left(\xi p_{\xi }+\eta p_{\eta }\right)}^2-2\left(\xi p_{\xi }+\eta p_{\eta }\right)=0,$ (2.1)

其中 $b\left(p\right)=-\frac{{\rho }^{″}\left(p\right)}{\rho \left(p\right)}=\frac{a^{\prime }\left(p\right)}{a\left(p\right)}$，(2.1)的特征值是

${\Lambda }_{\pm }={\lambda }_{\pm }=\frac{\xi \eta \pm \sqrt{a\left({\xi }^2+{\eta }^2-a\right)}}{{\xi }^2-a}.$ (2.2)

2.1. 四个角变量

在这里，我们使用了倾角变量 $\alpha ,\beta$ [8] ，它首次提出是在Courant和Friedrichs的专著中 [2] ，同时流角可以被定义为 $\sigma :=\left(\alpha +\beta \right)/2$，并且马赫角 $\omega :=\left(\alpha -\beta \right)/2$，我们可以用这些变量表示 $\left(\xi ,\eta \right)$ 为

$\xi =-\sqrt{a}\frac{\cos \sigma }{\sin \omega },\eta =-\sqrt{a}\frac{\sin \sigma }{\sin \omega }.$ (2.3)

注意到这与 [4] 的结果一致，现在我们再次推导细节。因为 $\tan \alpha ={\Lambda }_{+},\tan \beta ={\Lambda }_{-}$。

$\tan \alpha =\frac{\xi \eta +\sqrt{a\left({\xi }^2+{\eta }^2-a\right)}}{{\xi }^2-a},\tan \beta =\frac{\xi \eta -\sqrt{a\left({\xi }^2+{\eta }^2-a\right)}}{{\xi }^2-a}.$ (2.4)

对上述公式进行相减和相乘，我们有

$\tan \alpha -\tan \beta =\frac{2\sqrt{a\left({\xi }^2+{\eta }^2-a\right)}}{{\xi }^2-a},\tan \alpha \times \tan \beta =\frac{{\eta }^2-a}{{\xi }^2-a}.$ (2.5)

为了消除 ${\eta }^2$，我们注意到 ${\eta }^2-a=\tan \alpha \times \tan \beta \times \left({\xi }^2-a\right)$，并且得到

$\left(\tan \alpha -\tan \beta \right)\left({\xi }^2-a\right)=2\sqrt{a\left[{\xi }^2+\tan \alpha \times \tan \beta \times \left({\xi }^2-a\right)\right]}.$

然后我们有

$\frac{\xi }{\sqrt{a}}=\pm \frac{\cos \alpha \pm \cos \beta }{\sin \left(\alpha -\beta \right)}.$ (2.6)

虽然每种情况都是有意义的，但是为了方便，我们选择

$\frac{\xi }{\sqrt{a}}=-\frac{\cos \alpha +\cos \beta }{\sin \left(\alpha -\beta \right)}.$ (2.7)

最后将 $\alpha$ 和 $\beta$ 的表达式代入(2.7)，我们得到(2.3)的第一个方程，应用 $\left(\tan \alpha +\tan \beta \right)\left({\xi }^2-a\right)=2\xi \eta$，我们获得(2.3)的第二个方程。

2.2. 一阶特征形式

首先，我们引入一些基本符号

$\begin{array}{l}{\partial }^{+}={\partial }_{\xi }+{\Lambda }_{+}{\partial }_{\eta },{\partial }^{-}={\partial }_{\xi }+{\Lambda }_{-}{\partial }_{\eta },{\partial }^0=-\xi {\partial }_{\xi }-\eta {\partial }_{\eta },\\ {\bar{\partial }}^{+}=\cos \alpha {\partial }_{\xi }+\sin \alpha {\partial }_{\eta },{\bar{\partial }}^{-}=\cos \beta {\partial }_{\xi }+\sin \beta {\partial }_{\eta },\\ {\bar{\partial }}^0=\cos \sigma {\partial }_{\xi }+\sin \sigma {\partial }_{\eta },{\bar{\partial }}^{\perp }=\sin \sigma {\partial }_{\xi }-\cos \sigma {\partial }_{\eta }.\end{array}$ (2.8)

因此，我们有

$\begin{array}{l}{\bar{\partial }}^{+}=\cos \alpha {\partial }^{+},{\bar{\partial }}^{-}=\cos \beta {\partial }^{-},{\bar{\partial }}^0=\frac{{\partial }^0}{\sqrt{{\xi }^2+{\eta }^2}},\\ {\bar{\partial }}^{+}+{\bar{\partial }}^{-}=2\cos \omega {\bar{\partial }}^0,{\bar{\partial }}^{+}-{\bar{\partial }}^{-}=-2\sin \omega {\bar{\partial }}^{\perp }.\end{array}$ (2.9)

性质2.1 对于非线性波动系统(1.1)，有下式成立

$\begin{array}{l}{\bar{\partial }}^{\pm }\omega =\frac{{\sin }^2\omega }{\sqrt{a}}+\frac{b\tan \omega }{2}{\bar{\partial }}^{\pm }p,{\bar{\partial }}^{\pm }\sigma =\mp \frac{{\sin }^2\omega }{\sqrt{a}},\\ {\bar{\partial }}^{-}\alpha =\frac{2{\sin }^2\omega }{\sqrt{a}}+\frac{b\tan \omega }{2}{\bar{\partial }}^{-}p,{\bar{\partial }}^{+}\alpha =\frac{b\tan \omega }{2}{\bar{\partial }}^{+}p,\\ {\bar{\partial }}^{+}\beta =-\frac{2{\sin }^2\omega }{\sqrt{a}}-\frac{b\tan \omega }{2}{\bar{\partial }}^{+}p,{\bar{\partial }}^{-}\beta =-\frac{b\tan \omega }{2}{\bar{\partial }}^{-}p,\\ {\bar{\partial }}^{\perp }\sigma =\frac{\sin \omega }{\sqrt{a}},{\bar{\partial }}^0\sigma =0.\end{array}$ (2.10)

证明：证明的方法以前已经介绍 [7] ，因此对我们来说很容易证明这些公式，我们首先证明 ${\bar{\partial }}^{\pm }\sigma$ 和 ${\bar{\partial }}^{\pm }\omega$，微分公式(2.3)，我们有

${\bar{\partial }}^{\pm }\xi =-\frac{a^{\prime }{\bar{\partial }}^{\pm }p}{2\sqrt{a}}\frac{\cos \sigma }{\sin \omega }+\sqrt{a}\frac{\sin \sigma \sin \omega {\bar{\partial }}^{\pm }\sigma +\cos \sigma \cos \omega {\bar{\partial }}^{\pm }\omega }{{\sin }^2\omega },$ (2.11)

${\bar{\partial }}^{\pm }\eta =-\frac{a^{\prime }{\bar{\partial }}^{\pm }p}{2\sqrt{a}}\frac{\sin \sigma }{\sin \omega }-\sqrt{a}\frac{\cos \sigma \sin \omega {\bar{\partial }}^{\pm }\sigma -\sin \sigma \cos \omega {\bar{\partial }}^{\pm }\omega }{{\sin }^2\omega }.$ (2.12)

结合(2.11)和(2.12)，我们得到

$\begin{array}{l}\cos \left(\alpha -\sigma \right)=-\frac{a^{\prime }{\bar{\partial }}^{+}p}{2\sqrt{a}}\frac{1}{\sin \omega }+\sqrt{a}\frac{\cos \omega }{{\sin }^2\omega }{\bar{\partial }}^{+}\omega ,\\ \cos \left(\beta -\sigma \right)=-\frac{a^{\prime }{\bar{\partial }}^{-}p}{2\sqrt{a}}\frac{1}{\sin \omega }+\sqrt{a}\frac{\cos \omega }{{\sin }^2\omega }{\bar{\partial }}^{-}\omega .\end{array}$

通过计算发现

${\bar{\partial }}^{\pm }\omega =\frac{{\sin }^2\omega }{\sqrt{a}}+\frac{b\tan \omega }{2}{\bar{\partial }}^{\pm }p.$ (2.13)

同理，我们有

${\bar{\partial }}^{\pm }\sigma =\mp \frac{{\sin }^2\omega }{\sqrt{a}}.$ (2.14)

由于 $\alpha =\sigma +\omega ,\beta =\sigma -\omega$，所以 ${\bar{\partial }}^{\pm }\alpha ,{\bar{\partial }}^{\pm }\beta$ 的结果也可以获得，根据(2.9)，我们可以直接得到余下公式的证明。

3. 特征分解

这一节，我们将给出变量 $p,\alpha ,\beta$ 的二阶特征分解，其中p的分解是最重要的。

定理3.1 压力p在非线性波动系统中满足

$\{\begin{array}{l}{\bar{\partial }}^{-}{\bar{\partial }}^{+}p={\partial }^{+}p\left(\frac{b}{4{\cos }^2\omega }{\partial }^{+}p+\left(\frac{b}{2}+\frac{b}{4{\cos }^2\omega }\right){\partial }^{-}p+\frac{\sin 2\omega }{\sqrt{a}}\right),\\ {\bar{\partial }}^{+}{\bar{\partial }}^{-}p={\partial }^{-}p\left(\frac{b}{4{\cos }^2\omega }{\partial }^{-}p+\left(\frac{b}{2}+\frac{b}{4{\cos }^2\omega }\right){\partial }^{+}p+\frac{\sin 2\omega }{\sqrt{a}}\right).\end{array}$ (3.1)

证明：回顾(2.8)中 ${\bar{\partial }}^{\pm }$ 的定义，我们获得

$p_{\xi }=\frac{\sin \alpha {\bar{\partial }}^{-}p-\sin \beta {\bar{\partial }}^{+}p}{\sin 2\omega },p_{\eta }=\frac{\cos \beta {\bar{\partial }}^{+}p-\cos \alpha {\bar{\partial }}^{-}p}{\sin 2\omega }.$ (3.2)

和

$\begin{array}{l}{\bar{\partial }}^{-}{\bar{\partial }}^{+}p=\left(cos\beta {\partial }_{\xi }+sin\beta {\partial }_{\eta }\right)\left(cos\alpha {\partial }_{\xi }+sin\alpha {\partial }_{\eta }\right)p\\ =\left(-sin\alpha p_{\xi }{\bar{\partial }}^{-}\alpha +\cos \alpha p_{\eta }{\bar{\partial }}^{-}\alpha \right)+\left(cos\alpha {\bar{\partial }}^{-}{p}_{\xi }+\sin \alpha {\bar{\partial }}^{-}{p}_{\eta }\right).\end{array}$ (3.3)

将(3.2)代入(3.3)，我们有

$-sin\alpha p_{\xi }{\bar{\partial }}^{-}\alpha +\cos \alpha p_{\eta }{\bar{\partial }}^{-}\alpha =-\frac{b\tan \omega }{2\sin 2\omega }{\left({\bar{\partial }}^{-}p\right)}^2+\frac{b\tan \omega }{2\tan 2\omega }{\bar{\partial }}^{-}p{\bar{\partial }}^{+}p+\frac{2{\sin }^2\omega }{\sqrt{a}\tan 2\omega }{\bar{\partial }}^{+}p-\frac{2{\sin }^2\omega }{\sqrt{a}\sin 2\omega }{\bar{\partial }}^{-}p.$ (3.4)

和

$\begin{array}{c}cos\alpha {\bar{\partial }}^{-}{p}_{\xi }+\sin \alpha {\bar{\partial }}^{-}{p}_{\eta }=\cos \alpha \cos \beta \left(p_{\xi \xi }+\left(tan\alpha +tan\beta \right)p_{\xi \eta }+tan\alpha tan\beta p_{\eta \eta }\right)\\ =\frac{\cos \alpha \cos \beta }{a-{\xi }^2}\left(\left(a-{\xi }^2\right)p_{\xi \xi }-2\xi \eta p_{\xi \eta }+\left(a-{\eta }^2\right)p_{\eta \eta }\right)\\ =\frac{b}{4{\cos }^2\omega }{\left({\bar{\partial }}^{+}p+{\bar{\partial }}^{-}p\right)}^2+\frac{2{\sin }^2\omega }{\sqrt{a}\sin 2\omega }\left({\bar{\partial }}^{+}p+{\bar{\partial }}^{-}p\right).\end{array}$ (3.5)

然后我们将(3.4)和(3.5)代入(3.3)得到

$\begin{array}{l}{\bar{\partial }}^{-}{\bar{\partial }}^{+}p=\frac{b}{4{\cos }^2\omega }{\left({\bar{\partial }}^{+}p\right)}^2+\left(\frac{b\tan \omega }{2\tan 2\omega }+\frac{b}{2{\cos }^2\omega }\right){\bar{\partial }}^{-}p{\bar{\partial }}^{+}p+\frac{2{\sin }^2\omega \left(\cos 2\omega +1\right)}{\sqrt{a}\sin 2\omega }{\bar{\partial }}^{+}p{\bar{\partial }}^{+}p\\ +\left(-\frac{2{\sin }^2\omega }{\sqrt{a}\sin 2\omega }+\frac{2{\sin }^2\omega }{\sqrt{a}\sin 2\omega }\right){\bar{\partial }}^{-}p+\left(\frac{b\tan \omega }{2\sin 2\omega }+\frac{b}{4{\cos }^2\omega }\right){\left({\bar{\partial }}^{-}p\right)}^2\\ =\frac{b}{4{\cos }^2\omega }{\left({\bar{\partial }}^{+}p\right)}^2+\left(\frac{b}{2}+\frac{b}{4{\cos }^2\omega }\right){\bar{\partial }}^{-}p{\bar{\partial }}^{+}p+\frac{\sin 2\omega }{\sqrt{a}}{\bar{\partial }}^{+}p\\ ={\bar{\partial }}^{+}p\left(\frac{b}{4{\cos }^2\omega }{\bar{\partial }}^{+}p+\left(\frac{b}{2}+\frac{b}{4{\cos }^2\omega }\right){\bar{\partial }}^{-}p+\frac{\sin 2\omega }{\sqrt{a}}\right).\end{array}$ (3.6)

${\bar{\partial }}^{+}{\bar{\partial }}^{-}p$ 类似可得。

我们现在返回来考虑系统(1.3)的第二个和第三个方程，它们可以写成

$\{\begin{array}{l}{\partial }^0\left(\rho u\right)+p_{\xi }=0,\\ {\partial }^0\left(\rho v\right)+p_{\eta }=0.\end{array}$ (3.7)

通过一系列推导，我们可以计算出 $\left(u,v\right)$。

进一步，我们使用定理3.1可以获得 $\alpha ,\beta$ 的二阶特征分解。

定理3.2 对于变量 $\alpha$ 和 $\beta$，我们有以下二阶特征分解

$\{\begin{array}{l}{\bar{\partial }}^{-}{\bar{\partial }}^{+}\alpha +M_1{\bar{\partial }}^{+}\alpha =0,\\ {\bar{\partial }}^{+}{\bar{\partial }}^{-}\beta +M_2{\bar{\partial }}^{-}\beta =0,\\ {\bar{\partial }}^{+}{\bar{\partial }}^{-}\alpha +M_3{\bar{\partial }}^{-}\alpha =\left(-\frac{2b^{\prime }\sin 2\omega }{\sqrt{a}{b}^2}-\frac{3\tan \omega }{\sqrt{a}}\right){\bar{\partial }}^{+}\alpha ,\\ {\bar{\partial }}^{-}{\bar{\partial }}^{+}\beta +M_4{\bar{\partial }}^{+}\beta =\left(-\frac{2b^{\prime }\sin 2\omega }{\sqrt{a}{b}^2}-\frac{3\tan \omega }{\sqrt{a}}\right){\bar{\partial }}^{-}\beta .\end{array}$ (3.8)

$\begin{array}{l}{M}_1=-\frac{1}{\sin 2\omega }{\bar{\partial }}^{+}\alpha -\left(\frac{2b^{\prime }}{b^2\tan \omega }+\frac{\cos 2\omega +4}{\sin 2\omega }\right){\bar{\partial }}^{-}\alpha +\frac{2b^{\prime }\sin 2\omega }{\sqrt{a}{b}^2}+\frac{2\tan \omega }{\sqrt{a}},\\ M_2=-\frac{1}{\sin 2\omega }{\bar{\partial }}^{-}\beta +\left(\frac{2b^{\prime }}{b^2\tan \omega }+\frac{\cos 2\omega +4}{\sin 2\omega }\right){\bar{\partial }}^{+}\beta -\frac{2b^{\prime }\sin 2\omega }{\sqrt{a}{b}^2}-\frac{2\tan \omega }{\sqrt{a}},\\ M_3=-\frac{1}{\sin 2\omega }{\bar{\partial }}^{-}\alpha -\left(\frac{2b^{\prime }}{b^2\tan \omega }+\frac{\cos 2\omega +4}{\sin 2\omega }\right){\bar{\partial }}^{+}\alpha +\frac{\tan \omega }{\sqrt{a}}-\frac{\sin 2\omega }{\sqrt{a}},\\ M_4=-\frac{1}{\sin 2\omega }{\bar{\partial }}^{+}\beta +\left(\frac{2b^{\prime }}{b^2\tan \omega }+\frac{\cos 2\omega +4}{\sin 2\omega }\right){\bar{\partial }}^{-}\beta +\frac{\tan \omega }{\sqrt{a}}-\frac{\sin 2\omega }{\sqrt{a}}.\end{array}$

证明：由性质2.1，我们有

$\{\begin{array}{l}{\bar{\partial }}^{+}p=\frac{2}{b\tan \omega }{\bar{\partial }}^{+}\alpha =-\frac{2}{b\tan \omega }{\bar{\partial }}^{+}\beta -\frac{2\sin 2\omega }{\sqrt{a}b},\\ {\bar{\partial }}^{-}p=-\frac{2}{b\tan \omega }{\bar{\partial }}^{-}\alpha -\frac{2\sin 2\omega }{\sqrt{a}b}=-\frac{2}{b\tan \omega }{\bar{\partial }}^{-}\beta .\end{array}$ (3.9)

由定理3.1，性质2.1和(3.9)，我们可以计算 ${\bar{\partial }}^{-}{\bar{\partial }}^{+}\alpha$

$\begin{array}{l}{\bar{\partial }}^{-}{\bar{\partial }}^{+}\alpha ={\bar{\partial }}^{-}\left(\frac{b\tan \omega }{2}{\bar{\partial }}^{+}p\right)\\ =\frac{1}{2}\left[\left(b^{\prime }{\bar{\partial }}^{-}p\tan \omega +\frac{b}{{\cos }^2\omega }{\bar{\partial }}^{-}\omega \right){\bar{\partial }}^{+}p+b\tan \omega {\bar{\partial }}^{-}{\bar{\partial }}^{+}p\right]\\ ={\bar{\partial }}^{+}\alpha \left[\frac{1}{\sin 2\omega }{\bar{\partial }}^{+}\alpha +\left(\frac{2b^{\prime }}{b^2\tan \omega }+\frac{\cos 2\omega +4}{\sin 2\omega }\right){\bar{\partial }}^{-}\alpha -\frac{2b^{\prime }\sin 2\omega }{\sqrt{a}{b}^2}-\frac{2\tan \omega }{\sqrt{a}}\right].\end{array}$ (3.10)

类似地我们有

${\bar{\partial }}^{+}{\bar{\partial }}^{-}\beta ={\bar{\partial }}^{-}\beta \left[-\frac{1}{\sin 2\omega }{\bar{\partial }}^{-}\beta -\left(\frac{2b^{\prime }}{b^2\tan \omega }+\frac{\cos 2\omega +4}{\sin 2\omega }\right){\bar{\partial }}^{+}\beta +\frac{2b^{\prime }\sin 2\omega }{\sqrt{a}{b}^2}+\frac{2\tan \omega }{\sqrt{a}}\right].$ (3.11)

以相同的方式可以计算 ${\bar{\partial }}^{+}{\bar{\partial }}^{-}\alpha$

$\begin{array}{l}{\bar{\partial }}^{+}{\bar{\partial }}^{-}\alpha ={\bar{\partial }}^{+}\left(\frac{2{\sin }^2\omega }{\sqrt{a}}+\frac{b\tan \omega }{2}{\bar{\partial }}^{-}p\right)\\ =\frac{2{\sin }^2\omega }{\sqrt{a}}{\bar{\partial }}^{+}\omega -\frac{a^{\prime }{\sin }^2\omega }{a\sqrt{a}}{\bar{\partial }}^{+}p+\frac{b^{\prime }\tan \omega }{2}{\bar{\partial }}^{+}p{\bar{\partial }}^{-}p+\frac{b}{2{\cos }^2\omega }{\bar{\partial }}^{+}\omega {\bar{\partial }}^{-}p+\frac{b\tan \omega }{2}{\bar{\partial }}^{+}{\bar{\partial }}^{-}p\\ ={\bar{\partial }}^{-}\alpha \left[\frac{1}{\sin 2\omega }{\bar{\partial }}^{-}\alpha +\left(\frac{2b^{\prime }}{b^2\tan \omega }+\frac{\cos 2\omega +4}{\sin 2\omega }\right){\bar{\partial }}^{+}\alpha -\frac{\tan \omega }{\sqrt{a}}+\frac{\sin 2\omega }{\sqrt{a}}\right]\\ +{\bar{\partial }}^{+}\alpha \left(-\frac{2b^{\prime }\sin 2\omega }{\sqrt{a}{b}^2}-\frac{3\tan \omega }{\sqrt{a}}\right).\end{array}$

同理可得

$\begin{array}{l}{\bar{\partial }}^{-}{\bar{\partial }}^{+}\beta ={\bar{\partial }}^{+}\beta \left[-\frac{1}{\sin 2\omega }{\bar{\partial }}^{+}\beta -\left(\frac{2b^{\prime }}{b^2\tan \omega }+\frac{\cos 2\omega +4}{\sin 2\omega }\right){\bar{\partial }}^{-}\beta -\frac{\tan \omega }{\sqrt{a}}+\frac{\sin 2\omega }{\sqrt{a}}\right]\\ +{\bar{\partial }}^{-}\beta \left(-\frac{2b^{\prime }\sin 2\omega }{\sqrt{a}{b}^2}-\frac{3\tan \omega }{\sqrt{a}}\right).\end{array}$

定理3.2证明完成。

同时，特征分解使我们得出以下结论。

定理3.3 在二维非线性波动系统的自相似平面上，任何与常状态相邻的双曲状态都是一个简单波区域。