捕食者具有Allee效应和其他食物来源的Leslie-Gower模型的稳定性分析

Stability Analysis of the Leslie-Gower Model for Predator with Allee Effect and Other Food Resource

摘要: 本文研究捕食者具有Allee效应和其他食物来源的Leslie-Gower模型的动力学性质。我们讨论了边界平衡点和正平衡点存在的条件和稳定性。说明了较大的Allee效应会破坏系统的稳定性。当捕食者具有其他食物来源时，系统的动力学性质会变得更加复杂，也就是捕食者具有其他食物来源可能会破坏系统的稳定性。最后通过数值模拟，发现系统会经历Hopf分支并产生极限环。

Abstract: This paper studies the dynamics of the Leslie-Gower model for predator with Allee effect and other food source. We discuss the existence conditions and stability of boundary equilibrium points and positive equilibria. It is shown that the larger Allee effect will destroy the stability of the system. When predators have other food sources, the dynamics of the system becomes more complex, that is, the presence of predators with other food sources may destabilize the system. Finally, through numerical simulation we find that the system experiences Hopf bifurcation and limit cycle exists.

1. 引言

本文考虑如下的捕食者具有Allee效应 [1] 和其他食物来源的Leslie-Gower [2] [3] 捕食食饵模型：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=r_{0}x\left(1-\frac{x}{K}\right)-\frac{qxy}{a_0+x},\\ \frac{\text{d}y}{\text{d}t}=\frac{s_{0}y}{y+{\beta }_0}\left(1-\frac{y}{x+c_0}\right),\end{array}$ (1)

其中 $x,y$ 分别表示食饵和捕食者t在时刻的种群密度， $r_0$ 表示食饵的出生率，K是食饵的承载能力，q表示捕食者的捕获率， $a_0$ 为半饱和常数， $s_0$ 为捕食者的内在增长率， ${\beta }_0$ 为Allee效应常数， $c_0$ 表示捕食者

有其他食物来源， $\frac{y}{y+{\beta }_0}$ 表示Allee效应函数，这一项也被称为弱Allee效应 [4]， $\frac{qx}{a_0+x}$ 为Holling-II功能性反应函数 [5]。

1931年，美国生态学家W. C. Allee提出了一种生物学现象，即Allee效应。它是指种群密度较低的情况，种群平均增长率与种群密度呈正相关关系。在捕食–食饵模型中，Allee效应可能发生在食饵种群、捕食者种群 [6] 或两个种群中。本文中，我们研究Allee效应对捕食者种群的影响。

众所周知，在自然界中，捕食者物种往往把许多物种作为食物来源，这样，如果一种资源稀缺，它可能需要其他食物资源来维持其生命。这样，学者 [7] [8] 就提出了捕食者具有其他食物来源的捕食–食饵系统，并分析了其动力学行为。

所以同时考虑Allee效应和捕食者有其他食物来源对Leslie-Gower捕食食饵模型的动力学性质的影响，我们提出了捕食者具有Allee效应和其他食物来源的Leslie-Gower捕食食饵系统(1)。接下来，我们分析模型(2)的稳定性，并与捕食者没有其他食物来源的系统做比较。

为了计算简便，我们对模型(1)做如下的无量纲变换：

$\bar{x}=\frac{x}{K},\bar{y}=\frac{y}{K},\bar{t}=qt,$

并用 $x,y,t$ 分别代替 $\bar{x},\bar{y},\bar{t}$，模型(1)变为如下的新系统：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=rx\left(1-x\right)-\frac{xy}{a+x},\\ \frac{\text{d}y}{\text{d}t}=\frac{sy}{y+\beta }\left(1-\frac{y}{x+c}\right),\end{array}$ (2)

其中

$r=\frac{r_0}{q},\text{}a=\frac{a_0}{K},\beta =\frac{{\beta }_0}{K},s=\frac{s_0}{qK},c=\frac{c_0}{K}$

和所有参数都是正常。

2. 平衡点的存在性和稳定性

容易知道系统(2)总是存在三个边界平衡点 $E_0\left(0,0\right)$， $E^{*}\left(1,0\right)$， $E_{*}\left(0,c\right)$。下面给出其稳定性。

定理2.1 $E_0$ 是不稳定的； $E^{*}$ 是一个鞍点；当 $r>\frac{c}{a}$ 时， $E_{*}$ 是不稳定的；当 $0<r<\frac{c}{a}$ 时， $E_{*}$ 是稳定的。

证明：系统(2)在平衡点 $E_0\left(0,0\right)$ 和 $E^{*}\left(1,0\right)$ 的Jacobian矩阵分别为

$J_{E_0}=\left(\begin{array}{cc}r& 0\\ 0& \frac{s}{\beta }\end{array}\right),J_{E^{*}}=\left(\begin{array}{cc}-r& -\frac{1}{a+1}\\ 0& \frac{s}{\beta }\end{array}\right),$

可以看出矩阵 $J_{E_0}$ 的两个特征值为 ${\lambda }_1=r>0$， ${\lambda }_2=\frac{s}{\beta }>0$，因此 $E_0$ 是一个不稳定的结点；矩阵 $J_{E^{*}}$ 的两个特征值为 ${\lambda }_1=-r<0$， ${\lambda }_2=\frac{s}{\beta }>0$，因此 $E^{*}$ 是一个鞍点。

另外，系统(2)在平衡点 $E_{*}\left(0,c\right)$ 的Jacobian矩阵为

$J_{E_{*}}=\left(\begin{array}{cc}r-\frac{c}{a}& 0\\ \frac{s}{c+\beta }& -\frac{s}{c+\beta }\end{array}\right),$

矩阵 $J_{E_{*}}$ 的两个特征值为 ${\lambda }_1=r-\frac{c}{a}$， ${\lambda }_2=-\frac{s}{c+\beta }<0$，当 $r>\frac{c}{a}$ 时， ${\lambda }_1>0$， $E_{*}$ 是不稳定的；当 $0<r<\frac{c}{a}$ 时， ${\lambda }_1<0$， $E_{*}$ 是稳定的。

定理2.1证毕。

接下来，我们分析系统(2)的正平衡点的情况。由系统(2)可知，正平衡点满足以下方程

$\begin{array}{l}r\left(1-x\right)-\frac{y}{a+x}=0,\\ 1-\frac{y}{x+c}=0.\end{array}$ (3)

由方程(3)的第二个式子可以得到 $y=x+c$。将 $y=x+c$ 代入方程(3)第一个式子得到

$f\left(x\right)=r{x}^2+Bx+C=0,$ (4)

其中 $B=ar-r+1$ 和 $C=c-ar$。方程(4)的判别式为：

$\Delta ={\left(ar-r+1\right)}^2+4a{r}^2-4rc.$

令

$c^{*}=\frac{{\left(ar-r+1\right)}^2+4a{r}^2}{4r},$

$x_1=\frac{-B-\sqrt{\Delta }}{2r},x_2=\frac{-B+\sqrt{\Delta }}{2r},x_3=\frac{-B}{2r},$

$y_i=x_i+c,i=1,2,3.$

下面分析正平衡点的存在性。当 $0<c<ar$ 时，即 $C<0$，方程(4)有一个正根 $x_2$。当 $ar<c<c^{*}$ 时，即 $\Delta >0$ 和 $C>0$，如果 $B<0$，方程(4)有两个正根 $x_1$ 和 $x_2$ ；如果 $B\ge 0$，方程(4)没有正根。当 $c=c^{*}$ (即 $\Delta =0$ )或者 $c=ar$ (即 $C=0$ )时，如果 $B<0$，方程(4)有一个正根 $x_2$ ；如果 $B\ge 0$，方程(4)没有正根；当 $c>c^{*}$ 时，即 $\Delta <0$，方程(4)没有根。并且有 $0<x_1<x^{*}<x_2<1$。所以系统(2)的正平衡点有如下定理。

定理2.2

1) 当 $0<c<ar$ 或者 $c=ar$ 且 $B<0$ 成立时，则系统(2)有一个正平衡点 $E_2\left(x_2,y_2\right)$。

2) 当 $ar<c<c^{*}$ 和 $B<0$ 成立时，则系统(2)有两个正平衡点 $E_1\left(x_1,y_1\right)$ 和 $E_2\left(x_2,y_2\right)$。

3) 当 $c=c^{*}$ 和 $B<0$ 成立时，则系统(2)有一个正平衡点 $E_3\left(x_3,y_3\right)$。

4) 当 $c>c^{*}$ 成立时，则系统(2)没有正平衡点。

下面分析正平衡点的稳定性。首先令

$s^{*}=\frac{x_3\left(y_3+\beta \right)\left(y_3-r{\left(x_3+a\right)}^2\right)}{{\left(x_3+a\right)}^2},$

和

$s_{*}=\frac{x_2\left(y_2+\beta \right)\left(y_2-r{\left(x_2+a\right)}^2\right)}{{\left(x_2+a\right)}^2}.$

定理2.3当 $ar<c<c^{*}$ 和 $B<0$ 成立时，则系统(2)的正平衡点 $E_1\left(x_1,y_1\right)$ 是鞍点。

证明：系统(2)在正平衡点 $E_1$ 的Jacobian矩阵为：

$J_{E_1}=\left(\begin{array}{cc}-r{x}_1+\frac{x_1{y}_1}{{\left(x_1+a\right)}^2}& -\frac{x_1}{x_1+a}\\ \frac{s}{y_1+\beta }& -\frac{s}{y_1+\beta }\end{array}\right),$

其中 $y_1=c+x_1$。通过计算有

$Det{J}_{E_1}=\frac{s{x}_1\left(r{x}_1^2+2ar{x}_1+a^{2}r+a-c\right)}{{\left(a+x_1\right)}^2\left(y_1+\beta \right)}.$

由方程(4)有 $f\left(x_1\right)=0$，即有 $c=-r{x}_1^2-\left(ar-r+1\right)x_1+ar$，代入上式，可得

$Det{J}_{E_1}=\frac{s{x}_1\left(2r{x}_1+ar-r+1\right)}{\left(a+x_1\right)\left(y_1+\beta \right)}=-\frac{s{x}_1\sqrt{\Delta }}{\left(a+x_1\right)\left(y_1+\beta \right)}<0.$

显而易见， $E_1\left(x_1,y_1\right)$ 是一个鞍点。

定理2.3证毕。

定理2.4当 $0<c<ar$ 或者 $ar\le c<c^{*}$ 且 $B<0$ 成立时，则系统(2)的正平衡点 $E_2\left(x_2,y_2\right)$ 有如下性质：

1) 当 $s>s_{*}>0$ 时， $E_2\left(x_2,y_2\right)$ 是一个稳定的双曲结点或焦点。

2) 当 $s<s_{*}$ 时， $E_2\left(x_2,y_2\right)$ 是一个不稳定的双曲结点或焦点。

3) 当 $s=s_{*}$ 时， $E_2\left(x_2,y_2\right)$ 是一个细焦点或中心。

证明：系统(2)在平衡点 $E_2$ 的Jacobian矩阵为：

$J_{E_2}=\left(\begin{array}{cc}-r{x}_2+\frac{x_2{y}_2}{{\left(x_2+a\right)}^2}& -\frac{x_2}{x_2+a}\\ \frac{s}{y_2+\beta }& -\frac{s}{y_2+\beta }\end{array}\right),$

其中 $y_2=c+x_2$。通过简单的计算，得到

$Det{J}_{E_2}=\frac{s{x}_2\left(r{x}_2^2+2ar{x}_2+a^{2}r+a-c\right)}{{\left(a+x_2\right)}^2\left(y_2+\beta \right)}.$

由方程(4)有 $f\left(x_2\right)=0$，即有 $c=-r{x}_2^2-\left(ar-r+1\right)x_2+ar$，代入上式有

$Det{J}_{E_2}=\frac{s{x}_2\left(2r{x}_2+ar-r+1\right)}{\left(a+x_2\right)\left(y_2+\beta \right)}=\frac{s{x}_2\sqrt{\Delta }}{\left(a+x_2\right)\left(y_2+\beta \right)}>0.$

下面计算有

$Tr{J}_{E_2}=-r{x}_2+\frac{x_2{y}_2}{{\left(x_2+a\right)}^2}-\frac{s}{\beta +y_2}=\frac{s_{*}-s}{\beta +y_2}.$

当 $s>s_{*}>0$ 时，有 $Tr{J}_{E_2}<0$，即 $E_2$ 是一个稳定的双曲结点或焦点；当 $s<s_{*}$ 时，有 $Tr{J}_{E_2}>0$，即 $E_2$ 是一个不稳定的双曲结点或焦点；当 $s=s_{*}$ 时，有 $Tr{J}_{E_2}=0$，即 $E_2$ 是一个细焦点或中心。

定理2.4证毕。

定理2.5当 $c=c^{*}$ 和 $B<0$ 成立时，则系统(2)有一个正平衡点 $E_3\left(x_3,y_3\right)$，而且：

1) 当 $s>s^{*}>0$， $E_3\left(x_3,y_3\right)$ 是吸引的鞍结点。

2) 当 $s<s^{*}$ 时， $E_3\left(x_3,y_3\right)$ 是排斥的鞍结点。

证明：系统(2)在平衡点 $E_3$ 的Jacobian矩阵为：

$J_{E_3}=\left(\begin{array}{cc}-r{x}_3+\frac{x_3{y}_3}{{\left(x_3+a\right)}^2}& -\frac{x_3}{x_3+a}\\ \frac{s}{y_3+\beta }& -\frac{s}{y_3+\beta }\end{array}\right),$

其中 $y_3=c+x_3$。通过简单的计算，得到

$Det{J}_{E_3}=\frac{s{x}_3\left(r{x}_3^2+2ar{x}_3+a{r}^2+a-c\right)}{{\left(a+x_3\right)}^2\left(y_3+\beta \right)}.$

类似上面的分析，有

$Det{J}_{E_3}=\frac{s{x}_3\left(2r{x}_3+ar-r+1\right)}{\left(a+x_3\right)\left(y_3+\beta \right)}=0.$

通过计算有

$Tr{J}_{E_3}=-r{x}_3+\frac{x_3{y}_3}{{\left(x_3+a\right)}^2}-\frac{s}{\beta +y_3}=\frac{s^{\text{*}}-s}{\beta +y_3}.$

接下来，只需要判断 $Tr{J}_{E_3}$ 的符号。首先做变换 $\left(x,y\right)=\left(X+x_3,Y+y_3\right)$，将平衡点 $E_3$ 移动到原点，系统(2)变为：

$\{\begin{array}{l}\stackrel{\dot{}}{X}=a_{10}X+a_{01}Y+a_{20}{X}^2+a_{11}XY+a_{02}{Y}^2+P_1\left(X,Y\right),\\ \stackrel{\dot{}}{Y}=b_{10}X+b_{01}Y+b_{20}{X}^2+b_{11}XY+b_{02}{Y}^2+Q_1\left(X,Y\right),\end{array}$ (5)

其中

$a_{10}=-\frac{ar-r+1}{ar+r+1},a_{01}=\frac{ar-r+1}{ar+r+1},a_{20}=\frac{r\left(a^2{r}^2+4ar-r^2+2r-1\right)}{{\left(ar+r+1\right)}^2},a_{11}=-\frac{4a{r}^2}{{\left(ar+r+1\right)}^2},$

$a_{02}=0,b_{10}=\frac{4sr}{\left(a^2{r}^2+2a{r}^2+4\beta r+r^2-1\right)},b_{01}=-\frac{4sr}{\left(a^2{r}^2+2a{r}^2+4\beta r+r^2-1\right)},$

$b_{20}=-\frac{16s{r}^2}{\left(a^2{r}^2+2a{r}^2+4\beta r+r^2-1\right)\left(ar+r+1\right)\left(ar+r-1\right)},$

$b_{11}=\frac{16s{r}^2\left(a^2{r}^2+2a{r}^2+8\beta r+r^2-1\right)}{\left(a^2{r}^2+2a{r}^2+4\beta r+r^2-1\right)\left(ar+r+1\right)\left(ar+r-1\right)},$

$b_{02}=-\frac{64s\beta r^3}{{\left(a^2{r}^2+2a{r}^2+4\beta r+r^2-1\right)}^2\left(ar+r+1\right)\left(ar+r-1\right)},$

且 $P_1\left(X,Y\right)$， $Q_1\left(X,Y\right)$ 是关于 $\left(X,Y\right)$ 在原点附近次数不低于3的解析函数。

然后，我们做另一个变换：

$\left(X,Y\right)=\left(a_{01}u+a_{10}v,-a_{01}u+b_{10}v\right),$

$\text{d}\tau =Tr{J}_{E_3}\text{d}t,$

则系统(5)变为：

$\{\begin{array}{l}\stackrel{\dot{}}{u}=c_{20}{u}^2+c_{11}uv+c_{02}{v}^2+P_2\left(u,v\right),\\ \stackrel{\dot{}}{v}=v+d_{20}{u}^2+d_{11}uv+d_{02}{v}^2+Q_2\left(u,v\right),\end{array}$

其中

$c_{20}=-\frac{a_{10}\left(a_{01}^2{b}_{20}-a_{01}{a}_{10}{b}_{11}+a_{01}{a}_{11}{b}_{10}-a_{02}{a}_{10}{b}_{10}+a_{10}^2{b}_{02}\right)}{a_{01}^2{b}_{10}+2a_{01}{a}_{10}{b}_{10}+a_{10}^3},$

$c_{11}=-\frac{2a_{01}{a}_{10}^2{b}_{20}+a_{10}{a}_{01}{b}_{10}{b}_{11}-a_{01}{a}_{11}{b}_{10}^2+2a_{02}{a}_{10}{b}_{10}^2-a_{10}^3{b}_{11}+a_{10}^2{a}_{11}{b}_{10}-2a_{10}^2{b}_{02}{b}_{10}}{a_{01}^2{b}_{10}+2a_{01}{a}_{10}{b}_{10}+a_{10}^3},$

$c_{02}=\frac{a_{02}{b}_{10}^3-a_{10}^3{b}_{20}-a_{10}^2{b}_{10}{b}_{11}+a_{10}{a}_{11}{b}_{10}^2-a_{10}{b}_{02}{b}_{10}^2}{a_{01}^2{b}_{10}+2a_{01}{a}_{10}{b}_{10}+a_{10}^3},$

$d_{20}=\frac{a_{01}^3{b}_{20}-a_{01}^2{a}_{10}{b}_{11}-a_{01}{a}_{10}^2{a}_{11}+a_{01}{a}_{10}^2{b}_{02}+a_{02}{a}_{10}^3}{a_{01}^2{b}_{10}+2a_{01}{a}_{10}{b}_{10}+a_{10}^3},$

$d_{11}=\frac{2a_{01}^2{a}_{10}{b}_{20}+a_{01}^2{b}_{10}{b}_{11}-a_{01}{a}_{10}^2{b}_{11}+a_{01}{a}_{10}{a}_{11}{b}_{10}-2a_{01}{a}_{10}{b}_{02}{b}_{10}-2a_{02}{a}_{10}^2{b}_{10}-a_{10}^3{a}_{11}}{a_{01}^2{b}_{10}+2a_{01}{a}_{10}{b}_{10}+a_{10}^3},$

$d_{02}=\frac{a_{01}{a}_{10}^2{b}_{20}+a_{01}{a}_{10}{b}_{10}{b}_{11}+a_{01}{b}_{02}{b}_{10}^2+a_{02}{a}_{10}{b}_{10}^2+a_{10}^2{a}_{11}{b}_{10}}{a_{01}^2{b}_{10}+2a_{01}{a}_{10}{b}_{10}+a_{10}^3},$

且 $P_2\left(u,v\right)$， $Q_2\left(u,v\right)$ 是关于 $\left(u,v\right)$ 在原点附近次数不低于3的解析函数。

经过计算， $u^2$ 的系数为：

$c_{20}=\frac{sr{B}^3}{{\left(ar+r-1\right)}^3{\left(Tr{J}_{E_3}\right)}^2{s}^{*}}.$

由 $B=ar-r+1<0$ 可以推出 $ar+r-1>0$，则 $c_{20}<0$。由定理7.1 [9]，平衡点 $E_3$ 是一个鞍结点。当 $s>s^{*}>0$ 时，则 $Tr{J}_{E_3}<0$，即 $E_3\left(x_3,y_3\right)$ 是吸引的鞍结点；当 $s<s^{*}$ 时，则 $Tr{J}_{E_3}>0$，即 $E_3\left(x_3,y_3\right)$ 是排斥的鞍结点。定理2.5证毕。

由定理2.2得到若 $B<0$ 成立，当 $ar<c<c^{*}$ 时，则系统(2)有两个正平衡点 $E_1$ 和 $E_2$。当 $c=c^{*}$ 时，则系统(2)有一个正平衡点 $E_3$。当 $c>c^{*}$ 时，则系统(2)没有正平衡点。所以，系统(2)在 $c=c^{*}$ 会发生鞍结分支，则有：

注2.1 若 $B<0$ 成立，系统(2)在正平衡点 $E_3\left(x_3,y_3\right)$ 会发生鞍结分支，分支参数为 $c=c^{*}=c_{SN}$。

由定理2.3有，当 $ar<c<c^{*}$ 和 $B<0$ 成立时，则系统(2)有两个正平衡点 $E_1$ 和 $E_2$，且 $E_1$ 是一个鞍点。当 $s=s_{*}$ 时， $E_2$ 是一个细焦点或中心，此时， $Det{J}_{E_2}>0$ 和 $Tr{J}_{E_2}=0$，所以，正平衡点 $E_2$ 的Jacobian矩阵的特征值是一对纯虚根。另外，通过简单的计算可知

${\frac{\text{d}Tr{J}_{E_2}}{\text{d}s}|}_{s=s_{*}}=-\frac{1}{y_2+\beta }\ne 0,$

即满足Hopf分支横截性条件。综上所述，系统(2)在正平衡点 $E_2$ 附近发生Hopf分支且 $s=s_{*}$ 作为分支参数。

3. 数值模拟

例3.1 系统(2)中取 $a=\frac{1}{2}$， $r=3$， $\beta =1$，则令 $c=c^{*}=\frac{73}{48}$，此时满足

$B=-\frac{1}{2}<0,s^{*}=\frac{\text{125}}{\text{336}}.$

下面令 $s=\frac{200}{336}$，即 $s>s^{*}$，满足定理2.5条件，则正平衡点 $E_3$ 是吸引的鞍结点(见图1)。令 $s=\frac{50}{336}$，即 $s<s^{*}$，满足定理2.5条件，则正平衡点 $E_3$ 是排斥的鞍结点(见图2)。

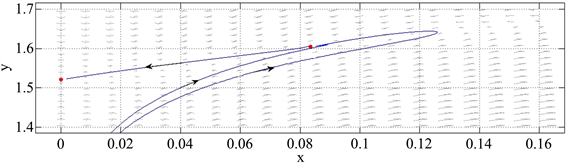
Figure 1. Positive equilibrium E₃ is a saddle-node

图1. 正平衡点E₃是鞍结点

Figure 2. Positive equilibrium E₃ is a saddle-node

图2. 正平衡点E₃是鞍结点

例3.2 系统(2)中取 $a=0.1$， $r=1.5$， $\beta =1$，则令 $c=0.155<c^{*}=0.17$， $s^{*}=0.75$ 此时满足

$B=-0.35<0,\text{}\text{}ar<c<c^{*}.$

令 $s=0.62<s^{*}$，根据定理2.4，可知系统(2)的正平衡点 $E_2\left(0.22,0.39\right)$ 是不稳定，同时在 $E_2$ 的邻域内产生超临界的Hopf分支且在 $E_2$ 附近出现一个极限环(见图3)。

当 $c=0$ (其它参数保持不变)，也就是系统(2)不考虑其它食物来源时，系统只有唯一的正平衡点 $\left(0.45,0.45\right)$，图4表示这个正平衡点是全局渐近稳定的。所以如果考虑其它食物来源(如图1)，会导致系统的动力学性质变得复杂，出现两个正平衡，其中一个正平衡点是鞍点，另一个正平衡点是不稳定的，而且会产生极限环。

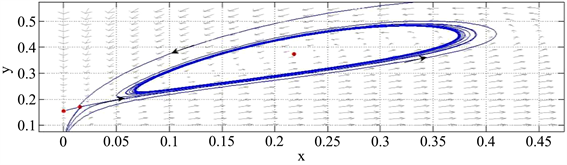
Figure 3. There exist a stable limit cycle around E₂

图3. 正平衡点E₂附近出现了一个稳定的极限环

Figure 4. Positive equilibrium is stable

图4. 正平衡点是稳定的

4. 结论

本文中，我们分析了捕食者具有Allee效应和其他食物来源的Leslie-Gower捕食–食饵系统的动力学行为。由定理2.1和2.2可知，平衡点的存在和Allee效应参数 $\beta$ 无关，同时注意 $s_{*}$ 随着 $\beta$ 的增大而增大。所以由定理2.3和2.4可知，保持其它参数不变，只增大Allee效应，会使得正平衡点 $E_2$ 从稳定变成不稳定，也就是较大的Allee效应会破坏系统(2)的稳定性。同时我们的研究也表明，与捕食者没有其他食物来源(即 $c=0$ 时比较)，系统只有一个边界平衡点和一个正平衡点。而当捕食者具有其他食物来源，(即 $c>0$ 时)，系统的动力学行为变得更加复杂，此时发现系统(2)有三个边界平衡点和两个正平衡点，其中正平衡点 $E_1$ 是鞍点，正平衡点 $E_2$ 可能稳定或不稳定，并且系统(2)可能会产生Hopf分支和出现极限环，也就是捕食者具有其他食物来源可能会破坏系统的稳定性。当只有一个正平衡点 $E_3$ 时，这个正平衡点是鞍结点，同时系统(2)也会经历鞍结分支。