《运筹学》中动态规划逆推算法理论拓展研究

Research on Theory Expansion of Backward Inference Algorithm of Dynamic Programming in Operations Research

摘要: 动态规划对于解决多阶段决策问题有明显效果。由于各种多阶段决策问题，往往具有不同的特点，比如，阶段有限或无限，一定或不定，时间参数离散或连续，决策过程确定或随机等，因此动态规划有多种模型。本文针对阶段数有限的离散确定性过程问题进行讨论。探讨其相应的逆推算法主要的数学思维，并进一步将相关知识点与思政教育相结合，拓展了动态规划逆推算法的理论体系。

Abstract: Dynamic programming has obvious effects on solving multi-stage decision-making problems. Since various multi-stage decision-making problems often have different characteristics, such as limited or unlimited stages, certain or indeterminate, discrete or continuous time parameters, and definite or random decision-making processes, so there are many models for dynamic programming. This article discusses the discrete deterministic process with a limited number of stages, discusses the main mathematical thinking of the corresponding reverse calculation algorithm, further combines the relevant knowledge points with ideological and political education, and expands the theoretical system of the dynamic programming reverse calculation algorithm.

1. 绪论

一般来说，只要问题可以划分成规模更小的子问题，并且原问题的最优解中包含了子问题的最优解，则可以考虑用动态规划解决。动态规划的实质是分治思想和解决冗余 [1]，因此动态规划的大致思路是把一个复杂的问题转化成一个分阶段逐步递推的过程，从简单的初始状态一步一步递推，最终得到复杂问题的最优解 [2]。在全国高校思想政治工作会议上，习近平总书记在会上强调，高校思想政治工作关系高校培养什么样的人、如何培养人以及为谁培养人这个根本问题。要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面 [3]。本文借助动态规划逆推算法的知识内容，把思政教育之“盐”融入在课程体系中，通过潜移默化、润物细无声的方式，让学习者在进行动态规划学习中，提升自身的德育水平。

2. 动态规划逆推算法及理论探究

接下来我们以《运筹学》动态规划逆推算法这一教学内容为例，详细说明如何从教学内容切入挖掘课程思政内容。

2.1. 动态规划逆推算法知识点

应用动态规划方法——逆序递推方法求解见图1中从A城市到E城市的最短路。连线上的数字表示两城市间的距离。

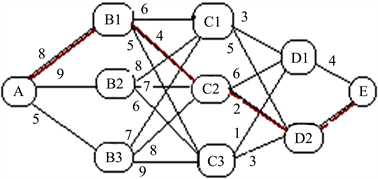
Figure 1. The shortest route from City A to City E

图1. 从A城市到E城市的最短路

这是一个四阶段的决策问题，可分为四步来进行：

Step 1，从k = 4开始，状态变量S₄可以取到D₁，D₂两种状态，它们到E点的距离分别为4和3，也即由D₁和D₂到终点E的最短距离，也就是， $f_4\left(D_1\right)=4$， $f_4\left(D_2\right)=3$。

Step 2，k = 3， $S_3=\left\{C_1,C_2,C_3\right\}$ 这里需经过一个中间点才能到达终点E的二级决策问题。为方便，规定： $d\left(S_k,U_k\right)$ 表示由状态 $S_k$ 出发采用决策 $U_k$ 到达下一阶段状态 $S_{k+1}$ 时的两点距离。显然从 $C_1$ 到E有两条路线可走，这里需加以比较，取其中最短距离为：

$f_3\left(C_1\right)=\min \left\{\begin{array}{c}d\left(C_1,D_1\right)+f_4\left(D_1\right)\\ d\left(C_1,D_2\right)+f_4\left(D_2\right)\end{array}\right\}=\min \left(\begin{array}{c}3+4\\ 5+3\end{array}\right)=7$

这样，可以得到，由C₁到E的最短距离7，其路径为 $C_1\to D_1\to E$，相应的决策为

$U_3\ast \left(C_1\right)=D_1$。

同样地，可以计算：

$f_3\left(C_2\right)=\min \left\{\begin{array}{c}d\left(C_2,D_1\right)+f_4\left(D_1\right)\\ d\left(C_2,D_2\right)+f_4\left(D_2\right)\end{array}\right\}=\min \left(\begin{array}{c}6+4\\ 2+3\end{array}\right)=5$

即从C₂到E的最短距离5，其路径为 $C_2\to D_2\to E$，相应的决策为

$U_3\ast \left(C_2\right)=D_2$。

计算

$f_3\left(C_3\right)=\min \left\{\begin{array}{c}d\left(C_3,D_1\right)+f_4\left(D_1\right)\\ d\left(C_3,D_2\right)+f_4\left(D_2\right)\end{array}\right\}=\min \left(\begin{array}{c}1+4\\ 3+3\end{array}\right)=5$

即从C₃到E的最短距离为5，其路径为 $C_3\to D_1\to E$，相应的决策为

$U_3\ast \left(C_3\right)=D_1$。

Step 3，k = 2，状态变量 $S_2=\left\{B_1,B_2,B_3\right\}$，由于第3段各点C₁，C₂，C₃到终点E的最短距离 $f_3\left(C_1\right)$ 、 $f_3\left(C_2\right)$ 、 $f_3\left(C_3\right)$ 已经求出，所以要求城市B₁到E的最短距离，只需要以它们为基础，分别加上B₁到达 C₁，C₂，C₃的一段距离，加以比较取其最短即可。也即计算

$f_2\left(B_1\right)=\min \left\{\begin{array}{c}d\left(B_1,C_1\right)+f_3\left(C_1\right)\\ d\left(B_1,C_2\right)+f_3\left(C_2\right)\\ d\left(B_1,C_3\right)+f_3\left(C_3\right)\end{array}\right\}=\min \left(\begin{array}{c}6+7\\ 4+5\\ 5+5\end{array}\right)=9$

这样可以得到，由B₁到E的最短距离为9，其路径为以 $B_1\to C_2\to D_2\to E$，相应的决策为

$U_2\ast \left(B_1\right)=C_2$。

同理可以计算

$f_2\left(B_2\right)=\min \left\{\begin{array}{c}d\left(B_2,C_1\right)+f_3\left(C_1\right)\\ d\left(B_2,C_2\right)+f_3\left(C_2\right)\\ d\left(B_2,C_3\right)+f_3\left(C_3\right)\end{array}\right\}=\min \left(\begin{array}{c}8+7\\ 7+5\\ 6+5\end{array}\right)=11$，

即

$U_2\ast \left(B_2\right)=C_3$。

计算

$f_2\left(B_3\right)=\min \left\{\begin{array}{c}d\left(B_3,C_1\right)+f_3\left(C_1\right)\\ d\left(B_3,C_2\right)+f_3\left(C_2\right)\\ d\left(B_3,C_3\right)+f_3\left(C_3\right)\end{array}\right\}=\min \left(\begin{array}{c}7+7\\ 8+5\\ 9+5\end{array}\right)=13$，

即

$U_2\ast \left(B_3\right)=C_2$。

Step 4，k = 1，只有一个状态点A，则计算：

$f_1\left(A_1\right)=\min \left\{\begin{array}{c}d\left(A,B_1\right)+f_2\left(B_1\right)\\ d\left(A,B_2\right)+f_2\left(B_2\right)\\ d\left(A,B_3\right)+f_2\left(B_3\right)\end{array}\right\}=\min \left(\begin{array}{c}8+9\\ 9+11\\ 5+13\end{array}\right)=17$

即

$U_1\ast \left(A\right)=B_1$。

所以，从城市A到城市E的最短距离为17。把各段的最优决策按计算顺序反项追踪，即可以得到最优决策序列，即 $U_1\ast \left(A\right)=B_1$， $U_2\ast \left(B_1\right)=C_2$， $U_3\ast \left(C_2\right)=D_2$， $U_4\ast \left(D_2\right)=E$，所以最短路线为 $A\to B_1\to C_2\to D_2\to E$。

归纳动态规划逆推算法的基本思想如下：

1) 将多阶段决策过程进行阶段划分，恰当地选取状态变量，决策变量和定义最优指标函数，从而把问题化成一族同类型的子问题，然后逐个求解这些子问题。

2) 求解时从边界条件开始，沿过程行进的方向，逐段递推寻优。在每一个子问题求解时，都要利用其前边已经求出的子问题的最优结果。最后一个子问题的最优解，就是整个问题的最优解。

3) 动态规划方法是既把当前一段与未来各段分开，又把当前效益和未来效益结合起来考虑的一种最优化方法。因此，每段的最优策略的选取都是从全局考虑的，它与该段的最优选择是不同的。

2.2. 动态规划逆推算法的数学思想

通过知识的讲解和升华，提炼出动态规划逆推算法的数学思想：

1) 局部与全局的思维。动态规划每个阶段都是局部，整个过程的最优，就是全局的最优，局部只是全局的一部分，每个局部也就是每个阶段的子问题找到了最优，才能实现全局的最优。

2) 化静为动的思想。逆推算法将整个求优过程按照时间或空间分为若干相互联系的阶段，将静态规划转化为动态规划，从而逐阶段求优在阶段运动过程中实现整个过程最优。

2.3. 动态规划逆推算法理论拓展研究

以动态规划逆推算法的知识点和思想为基础，我们深入探究这一动态规划经典算法，探究其蕴含的丰富的思政元素，归纳如下：

动态规划的逆推法的学习，能联想到这样一个故事：有一年，一群斗志昂扬的栋梁之材从美国哈佛大学毕业了。他们将要开始穿越他们自己的沼泽地。智力、学历、环境条件方面他们相差无几。临出校门前，哈佛大学对他们进调查了一次他们的人生目标。结果是这样的：他们中没有目标的占27%；目标含糊的占60%；有清晰但比较短期的目标占10%；有清晰而长远目标的占3%。

以后的25年中，他们各自打拼。25年后，哈佛再次跟踪调查了这群学生。结果是这样的：具有长远目标的3%的人，25年来他们朝着一个方向坚持不懈地努力，后来几乎都成为社会各界的成功人士，其中不乏行业领袖、社会精英等；具有短期目标的10%的人。25年来他们不断地实现各自的短期目标，大都生活在社会的中上层，成为各个领域的专业人士；目标含糊的60%的人，他们安稳地生活与工作。但都没有什么大的成绩，几乎都生活在社会的中下层；剩下没有目标的27%的人，过得很不如意，并且常常抱怨社会、抱怨他人、抱怨这个“不肯给他们机会”的世界。

而其实，他们的差别的主要在于：25年前，他们中的一些人知道为什么要穿越人生的沼泽地，而另一些目标不明确的人很笨不清楚或者不很清楚。

这也启示我们每个状态都有一个目标，要早定每个阶段的目标，也就是类似于我们动态规划的逆推算法，要早立志。从目标开始， 逐步逆推实现每个阶段的短期目标，以最短的路径达到我们的理想目标。

3. 小结

本文首先介绍了《运筹学》课程中的动态规划逆推算法，然后阐述了动态规划逆推算法的数学思想，再进一步针对这些数学思想进行了理论拓展，挖掘提炼出了其中蕴含的课程思政元素。实现了思政寓课程、课程融思政的理论探索。

总而言之，挖掘课程内容中的思政元素，是一项长期而艰巨的任务，在《运筹学》课程体系当中，具有丰富的思想价值值得深入地挖掘，需要不断地进行探索，从而更好地将课程思政落实到课程内容当中。

基金项目

2020年度上海市重点课程《系统工程导论》建设项目；2021年度上海市重点课程《运筹学》建设项目。