基于节点优先级服务的混合P2P网络性能分析

Performance Analysis of Hybrid P2P Networks Based on Node Priority Service

摘要: 本文为了抑制P2P网络中的“搭便车”现象，提高对等网络的服务质量，请求节点被分为高优先级请求节点和低优先级请求节点。提出了一种具有负顾客和异步休假策略的抢占优先M/M/c排队模型，通过拟生灭过程和矩阵几何解的方法求解系统的稳态分布。通过数值实验，分析系统性能指标随系统参数变化的趋势。最后构造两类请求节点的个人效益函数，结果表明高优先级请求节点的个人效益高于低优先级请求节点个人效益。

Abstract: In order to suppress the “free riding” phenomenon in P2P networks and improve the service quality of P2P networks, the requesting nodes are divided into high priority requesting nodes and low priority requesting nodes. A preemptive priority M/M/c queuing model with negative customers and asynchronous vacation strategy is proposed. The steady-state distribution of the system is solved by quasi birth-and-death process and matrix-geometric solution. Through numerical ex-periments, the change trend of system performance index with system parameters is analyzed. Finally, the personal expected return function of two types of request nodes is constructed. The results show that the personal expected income of high priority requesting nodes is higher than that of low priority requesting nodes.

1. 引言

P2P系统是一种分布式系统，部分或完全不需要中央服务器 [1]。是一个依赖于连接端节点的计算能力和带宽的系统，而不是集中式的。具有分布式控制、自组织和对称通信的特征。P2P系统有多种类型，主要用于大规模内容分发、文件共享、平台共享、通信、分布式计算和协作。在P2P系统中，由于使用系统和其他对等点的资源，对等方需要通过共享其资源来添加到系统中。然而，在众多P2P系统中，大量对等点不愿共享资源，只从系统中获取记录而不返回任何记录的客户端，称为搭便车者。

有几项测量研究证实了P2P网络中存在搭便车者。Handurukande等人 [2] 在edonkey进行的跟踪分析中，大约80%的对等点是搭便车的。Adar等人 [3] 测量研究结果表明，网络中25%的对等方提供了Gnutella中约99%的资源。此外，Asvanund等 [4] 发现在Gnutella 0.6中存在搭便车现象。搭便车降低了P2P系统的有效性、健壮性，加剧了网络拥塞，导致系统不稳定。统计数据显示，在Gnutella 0.6中，25%的节点提供了大约99%的资源，7%的节点贡献了比其他节点更多的文件 [5]。70%的对等点根本不共享任何文件，25%的对等点提供了99%的网络查询命中率 [6]。因此，为了提高P2P网络的服务质量，必须有效抑制搭便车行为。

目前，许多学者针对搭便车现象都提出了自己的解决方案。Shin等人 [7] 提出了一种通用的激励机制T-Chain，用于加强参与者之间的合作。T-Chain使合作成为强制性的，并允许新来者将他们的第一个接收文件上传到另一个对等方。T链的简单性促进了参与者之间的合作，并且可以很容易地适应其他应用或协议。Oualhad等人 [8] 提出了一种基于声誉的概率资源分配方案。为信誉较高的节点提供了选择偏好，同时也为彼此信誉不好的节点之间的交互提供了一定的有限概率。这避免了上述对等点之间的断开连接。Alotibi等人 [9] 提出了一种信用方法来防止P2P网络中的搭便车者。该方法使用基于点的免费搭车者检测来限制他们的活动，并通过提供下载优先级来奖励最合作的节点，以减少他们的下载时间。

本文提出一种节点优先级服务的策略来应对搭便车行。在实际应用中，请求节点根据其贡献值可分为低优先级请求节点和高优先级请求节点，高优先级请求节点抢占低优先级请求节点的服务，以此来减少低优先级请求节点的个人效益，提高网络运行的稳定性。研究P2P网络中具有负顾客和异步休假的抢占优先级M/M/c排队模型，建立了一个三维连续时间Markov随机模型。利用QBD过程和矩阵几何解构造系统性能指标，得到了排队模型的稳态分布，并通过数值实验分析了参数变化对P2P网络系统性能指标的影响。定义了个人效益函数，并详细分析了两类请求节点的个人效益。

2. 混合对等网络

本文所考虑的混合P2P网络模型是由集中式网络模型和分布式网络模型结合构成。如图1所示，分布式网络是由簇与簇之间连接组成的，而簇是一个小型的集中式网络，节点根据物理位置相近的原则组织在一起。簇中含有两种节点，一种是普通节点，另一种是超级节点。普通节点是网络中的请求节点，只有发布、查找资源信息和维护资源的基本能力。超级节点是一个服务节点，充当该簇中的资源服务器，接收来自节点的连接和资源处理请求，并将处理结果返回给请求节点。

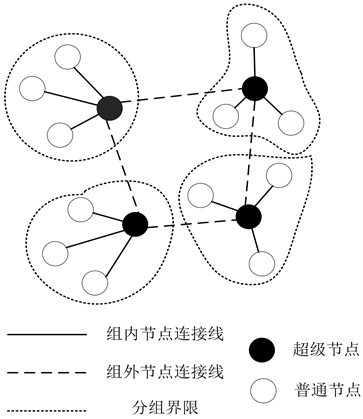
Figure 1. Node dynamic grouping diagram

图1. 节点动态分组示例

在此模型上，引入节点服务请求队列请求服务的概念。超级节点根据请求节点的贡献值将其划分到相应的队列，包括搭便车请求节点队列和合作请求节点队列。搭便车请求节点加入混合P2P网络后的主要目的是下载所需的资源。当它下载完资源时，就会离开网络，当它需要再次下载资源时，它会再次加入这个网络。合作请求节点不仅下载资源，还上传资源为其他节点服务，而且不频繁加入和离开混合P2P网络。为了鼓励节点更稳定地留在网络中，提高网络的服务质量，合作请求节点共享资源被优先考虑。合作请求节点队列的优先级高于搭便车请求节点队列。为了降低系统能耗，当没有节点请求服务时，簇中的服务节点会进行异步休假。

3. 建模分析

在混合对等网络中，将搭便车请求节点和合作请求节点抽象成两类顾客，两类请求节点请求服务的过程抽象为顾客到达的过程，将服务节点抽象为服务台，节点为用户服务的过程抽象为服务台服务的过程。

3.1. 模型描述

1) 假设搭便车请求节点和合作请求节点的到达间隔服从参数为 ${\lambda }_1,{\lambda }_2\left({\lambda }_1,{\lambda }_2>0\right)$ $\lambda \left(\lambda >0\right)$ 的指数分布。合作节请求点对搭便车请求节点具有抢占优先权，即当服务节点被搭便车请求节点占用且无空闲服务节点时，先到达的合作请求节点抢占正在服务的搭便车请求节点的服务，搭便车请求节点退回其队首处于等待状态，当所有服务节点均被合作请求节点占用时，新到达的合作请求节点需要等待排队。搭便车请求节点队列的容量无限，合作请求节点队列的空间最大容量为 $c$，若合作请求节点数量等于 $c$，新到的合作请求节点消失。

2) 簇中有 $c$ 个服务节点，并对搭便车请求节点和合作请求节点的服务时间分别服从参数为 ${\mu }_1,{\mu }_2\left({\mu }_1,{\mu }_2>0\right)$ 的指数分布。每当系统变成空闲时，服务节点恰好依次休假。休假结束时若系统中已有顾客等待，立刻开始为顾客服务并一直持续到系统再次空出。若休假结束时系统中无请求节点等待，服务节点进入通常的闲期，直到新的请求节点到达时再开始为其服务，由于每次服务完后服务节点仅有一次休假因此称这种策略下的排队系统为异步单重休假M/M/c/n + M排队系统。其中休假时间服从参数为 $\theta \left(\theta >0\right)$ 的指数分布。假设每个服务节点在工作期内的平均能耗为 $g_1$，在闲期内的平均能耗为 $g_2$，其中 $g_1>g_2>0$。

3) 由于网络系统环境、网络病毒等原因，会产生一些不利于簇的干扰因素，从而抵消一部分的传输数据，这种外来干扰即可看作负顾客，负顾客的抵消作用会对排队系统带来不同程度的影响。负顾客到达后即进入请求节点所在的队列尾部，其到达间隔服从参数为 $\epsilon$ 的负指数分布，按照先到先服务的排队规则，抵消一个队尾的请求节点，而负顾客本身并不接受服务，在休假期间自动消失。

4) 假设负顾客的到达间隔、两类请求节点的到达间隔、服务节点的服务时间等随机变量均相互独立，且同一类节点服从先到先服务的服务顺序。

3.2. 模型分析

3.2.1. 状态转移率分析

假设 $L_1\left(t\right)$ 表示在时刻 $t$ 搭便车请求节点的数量， $L_2\left(t\right)$ 表示在时刻 $t$ 合作请求节点的数量， $J\left(t\right)$ 表示系统在时刻 $t$ 休假的服务节点数， $J\left(t\right)=k\left(0\le k\le d\right)$ 表示在时刻 $t$ 有 $k$ 个请求节点在休假。则 $\left\{\left(L_1\left(t\right),L_2\left(t\right),J\left(t\right)\right),t\ge 0\right\}$ 是一个三维Markov过程，且有状态空间为

$\Omega =\left\{\left(i,j,k\right),i\ge 0,0\le j\le c,0\le k\le d\right\}$.

称所有可能的状态 $\left(i,0,0\right),\left(i,0,1\right),\left(i,1,0\right),\cdots ,\left(i,d,0\right),\left(i,1,0\right),\left(i,1,1\right),\cdots ,\left(i,1,d\right),\left(i,c,0\right),\left(i,c,1\right),\cdots ,\left(i,c,d\right)$ 为水平 $i$，其中 $i\ge 1$。将状态按字典顺序进行排列，系统的状态转移率矩阵可以改成如下形式：

$Q=\left[\begin{array}{ccccccccc}{A}_0& C& & & & & & & \\ B_1& A_1& C& & & & & & \\ & B_2& A_2& C& & & & & \\ & & \ddots & \ddots & \ddots & & & & \\ & & & B_{c-1}& A_{c-1}& C& & & \\ & & & & B_c& A_c& C& & \\ & & & & & B& A& C& \\ & & & & & & \ddots & \ddots & \ddots \end{array}\right]$

其中 $B_i\left(1\le i\le c\right)$ 和 $B_i\left(i\ge c+1\right)$ 表示从 $i$ 水平到 $i-1$ 水平的一步转移率矩阵， ${{\rm A}}_i\left(1\le i\le c-1\right)$ 和 $A_i=A\left(i\ge c\right)$ 表示从 $i$ 水平到 $i$ 水平的一步转移率矩阵， $C={\lambda }_1{{\rm I}}_1\left(i\ge 0\right)$ 表示从 $i$ 水平到 $i+1$ 水平的一步转移率矩阵，均为 $\left(c+1\right)\times \left(d+1\right)$ 维单位矩阵。

为了更加方便表达上述矩阵，定义 ${{\rm I}}_2$ 为 $d+1$ 维单位矩阵；定义方阵 $e_{i,j}\left(i\ge 0,0\le j\le c\right)$ 中的 $e_{i,j,k}$ 为状态 $\left(i,j,k\right)$ 到状态 $\left(i,j,k\right)$ 的转移率；定义方阵 $b_{i,j}\left(i\ge 1,0\le j\le c\right)$ 中的 $b_{i,j,k}$ 表示从状态 $\left(i,j,k\right)$ 到状态 $\left(i-1,j,k\right)$ 的转移率；定义方阵 $a_{i,j}\left(i\ge 1,0\le j\le c\right)$ 中的 $a_{i,j,k}$ 表示从状态 $\left(i,j,k\right)$ 到状态 $\left(i,j-1,k\right)$ 的转移率。

$B=\left[\begin{array}{cccccc}{b}_{i,0}& & & & & \\ & b_{i,1}& & & & \\ & & b_{i,2}& & & \\ & & & \ddots & & \\ & & & & b_{i,(c-1)}& \\ & & & & & b_{i,c}\end{array}\right]$, $C=\left[\begin{array}{cccc}{\lambda }_1{{\rm I}}_1& & & \\ & {\lambda }_1{{\rm I}}_1& & \\ & & \ddots & \\ & & & {\lambda }_1{{\rm I}}_1\end{array}\right]$,

$A=\left[\begin{array}{cccccc}{e}_{i,0}& {\lambda }_2{I}_2& & & & \\ a_{i,1}& e_{i,1}& {\lambda }_2{I}_2& & & \\ & a_{i,2}& e_{i,2}& {\lambda }_2{I}_2& & \\ & & \ddots & \ddots & \ddots & \\ & & & a_{i,\left(c-1\right)}& e_{i,\left(c-1\right)}& {\lambda }_2{I}_2\\ & & & & a_{i,c}& e_{i,c}\end{array}\right]$, $e_{i,j}=\left[\begin{array}{cccccc}{e}_{i,j,0}& & & & & \\ \theta & e_{i,j,1}& & & & \\ & 2\theta & e_{i,j,2}& & & \\ & & \ddots & \ddots & & \\ & & & \left(d-1\right)\theta & e_{i,j,\left(d-1\right)}& \\ & & & & d\theta & e_{i,j,d}\end{array}\right]$,

其中

$e_{i,j,0}=-{\lambda }_1-{\lambda }_2-\min \left(c-j\right){\mu }_2-\min \left(c-j,i\right){\mu }_1-2\epsilon ,0\le j<c$,

$e_{i,c,0}=-{\lambda }_1-c{\mu }_2$.

当 $1\le k\le d$，

$e_{i,j,k}=\{\begin{array}{l}-{\lambda }_1-{\lambda }_2-\min \left(c-k,j\right){\mu }_2-\min \left(c-k-j,i\right){\mu }_1-k\theta -\epsilon ,c-k-j>0,0\le j<c,\\ -{\lambda }_1-{\lambda }_2-\min \left(c-k,j\right){\mu }_2-k\theta ,c-k-j\le 0,0\le j<c,\end{array}$

$e_{i,j,c}=-{\lambda }_1-\left(c-k\right){\mu }_2-\epsilon -k\theta$.

1) 若 $0\le i+j\le c-d$，

$a_{i,j}=\left[\begin{array}{cccccc}0& a_{i,j,0}& & & & \\ & 0& a_{i,j,1}& & & \\ & & 0& a_{i,j,2}& & \\ & & & \ddots & \ddots & \\ & & & & 0& a_{i,j,\left(d-1\right)}\\ & & & & & a_{i,j,d}\end{array}\right]$,

$b_{i,j}=\left[\begin{array}{cccccc}0& b_{i,j,0}& & & & \\ & 0& b_{i,j,1}& & & \\ & & 0& b_{i,j,2}& & \\ & & & \ddots & \ddots & \\ & & & & 0& b_{i,j,\left(d-1\right)}\\ & & & & & b_{i,j,d}\end{array}\right]$,

其中

$a_{i,j,k}=\min \left(c-k,j\right){\mu }_2+\epsilon ,0\le k\le d$,

$b_{i,j,0}=\min \left(c-j,i\right){\mu }_1\text{+}\epsilon$,

$b_{i,j,k}=\min \left(c-k-j,i\right){\mu }_1+\epsilon ,1\le k\le d-1$,

$b_{i,j,d}=\min \left(c-d-j,i\right){\mu }_1+\epsilon ,c-d-j>0$.

2) 若 $c-d+1\le i+j\le c-1$,

$a_{i,j}=\left[\begin{array}{ccccccccc}0& a_{i,j,0}& & & & & & & \\ & 0& a_{i,j,1}& & & & & & \\ & & \ddots & \ddots & & & & & \\ & & & 0& a_{i,j,\left(c-i-j\right)}& & & & \\ & & & & a_{i,j,\left(c-i-j+1\right)}& 0& & & \\ & & & & & a_{i,j,\left(c-i-j+2\right)}& 0& & \\ & & & & & & \ddots & \ddots & \\ & & & & & & & a_{i,j,\left(d-1\right)}& 0\\ & & & & & & & & a_{i,j,d}\end{array}\right]$,

$b_{i,j}=\left[\begin{array}{ccccccccc}0& b_{i,j,0}& & & & & & & \\ & 0& b_{i,j,1}& & & & & & \\ & & \ddots & \ddots & & & & & \\ & & & 0& b_{i,j,\left(c-i-j\right)}& & & & \\ & & & & b_{i,j,\left(c-i-j+1\right)}& 0& & & \\ & & & & & b_{i,j,\left(c-i-j+2\right)}& 0& & \\ & & & & & & \ddots & \ddots & \\ & & & & & & & b_{i,j,\left(d-1\right)}& 0\\ & & & & & & & & b_{i,j,d}\end{array}\right]$,

其中

$a_{i,j,k}=\min \left(c-k,j\right){\mu }_2+\epsilon ,0\le k\le d$,

$b_{i,j,0}=\min \left(c-j,i\right){\mu }_1\text{+}\epsilon$,

$b_{i,j,k}=\{\begin{array}{l}\min \left(c-k-j,i\right){\mu }_1+\epsilon ,c-k-j>0,\\ 0,c-k-j\le 0.\end{array}$.

3) 若 $i+j=c$,

$a_{i,j}=\left[\begin{array}{cccccc}0& a_{i,j,0}& & & & \\ & a_{i,j,1}& 0& & & \\ & & & \ddots & \ddots & \\ & & & & a_{i,j,\left(d-1\right)}& 0\\ & & & & & a_{i,j,d}\end{array}\right]$,

$b_{i,j}=\left[\begin{array}{cccccc}0& b_{i,j,0}& & & & \\ & b_{i,j,1}& 0& & & \\ & & & \ddots & \ddots & \\ & & & & b_{i,j,\left(d-1\right)}& 0\\ & & & & & b_{i,j,d}\end{array}\right]$,

其中

$a_{i,j,k}=\min \left(c-k,j\right){\mu }_2+\epsilon ,0\le k\le d$,

$b_{i,j,0}=\min \left(c-j,i\right){\mu }_1\text{+}\epsilon$,

$b_{i,j,k}=\min \left(c-k-j,i\right){\mu }_1+\epsilon ,1\le k\le d$.

4) 若 $i+j\ge c+1$,

$a_{i,j}=\left[\begin{array}{ccccc}{a}_{i,j,0}& & & & \\ & a_{i,j,1}& & & \\ & & \ddots & & \\ & & & a_{i,j,\left(d-1\right)}& \\ & & & & a_{i,j,d}\end{array}\right]$,

$b_{i,j}=\left[\begin{array}{ccccc}{b}_{i,j,0}& & & & \\ & b_{i,j,1}& & & \\ & & \ddots & & \\ & & & b_{i,j,\left(d-1\right)}& \\ & & & & b_{i,j,d}\end{array}\right]$.

其中

$a_{i,j,k}=\min \left(c-k,j\right){\mu }_2+\epsilon ,0\le k\le d$,

$b_{i,j,0}=\min \left(c-j,i\right){\mu }_1\text{+}\epsilon$,

$b_{i,j,k}=\min \left(c-k-j,i\right){\mu }_1+\epsilon ,1\le k\le d$.

3.2.2. 模型稳态分析

由矩阵 $Q$ 的结构可知，Markov过程 $\left\{\left(L_1\left(t\right),L_2\left(t\right),J\left(t\right)\right),t\ge 0\right\}$ 是一个拟生灭过程(QBD)。当Markov过程 $\left\{\left(L_1\left(t\right),L_2\left(t\right),J\left(t\right)\right),t\ge 0\right\}$ 正常返时，其稳态分布为

${\pi }_{i,l,j}=\underset{t\to \infty }{\lim }P\left\{L_1\left(t\right)=i,L_2\left(t\right)=l,J\left(t\right)=j\right\},\left(i,l,j\right)\in \Omega$，

${\pi }_0=\left({\pi }_{0,0,0},{\pi }_{0,1,0},{\pi }_{0,1,1},\cdots ,{\pi }_{0,c,0},{\pi }_{0,c,1}\right)$，

${\pi }_i=\left({\pi }_{i,0,0},{\pi }_{i,0,1},{\pi }_{i,1,0}{\pi }_{i,1,1},\cdots ,{\pi }_{i,c,0},{\pi }_{i,c,1}\right),i\ge 1$，

$\Pi =\left({\pi }_0,{\pi }_1,{\pi }_2,\cdots \right)$.

QBD $\left\{\left(L_1\left(t\right),L_2\left(t\right),J\left(t\right)\right),t\ge 0\right\}$ 正常返的充分必要条件是矩阵方程 $R^{2}B+RA+C=0$ 存在最小非负解 $R$，谱半径 $SP\left(R\right)<1$，并且随机阵

$B\left[R\right]=\left[\begin{array}{ccccccc}{A}_0& C& & & & & \\ B_1& A_1& C& & & & \\ & B_2& A_2& C& & & \\ & & \ddots & \ddots & \ddots & & \\ & & & B_{c-1}& A_{c-1}& C& \\ & & & & B_c& A& C\\ & & & & & B& RB+A\end{array}\right]$

存在左零向量。当QBD正常返时，稳态分布满足如下方程组

$\{\begin{array}{l}\left({\pi }_0,{\pi }_1,\cdots ,{\pi }_c\right)B\left[R\right]=0,\\ {\displaystyle \underset{i=0}{\overset{c-1}{\sum }}{\pi }_{i}e+{\pi }_c{\left(I-R\right)}^{-1}e=1,}\\ {\pi }_i={\pi }_c{R}^{i-c},i\ge c.\end{array}$

其中 $e$ 是维数为 $\left(c+1\right)\left(d+1\right)$ 且所有元素均为1的列向量， $I$ 是维数为 ${\left(c+1\right)}^2\left(d+1\right)$ 单位矩阵。

对于上述分析证明过程，采用了文献 [10] [11] 中提到的矩阵–几何解的方法。矩阵的表达相对复杂，所以很难直接给出速率矩阵R的分析表达。因此，采用高斯–赛德尔迭代法来求出速率矩阵R的近似解。

3.3. 性能指标

根据上述分析可以得到各性能指标：

1) 搭便车请求节点的平均队长为

$E\left(L_1\right)={\displaystyle \underset{i=0}{\overset{\infty }{\sum }}iP\left(L_1=i\right)}={\displaystyle \underset{i=1}{\overset{\infty }{\sum }}i}\left({\displaystyle \underset{j=0}{\overset{c}{\sum }}{\displaystyle \underset{k=0}{\overset{d}{\sum }}{\pi }_{i,j,k}}}\right)$.

2) 合作请求节点的平均队长为

$E\left(L_2\right)={\displaystyle \underset{j=0}{\overset{c}{\sum }}jP\left(L_2=j\right)}={\displaystyle \underset{i=0}{\overset{\infty }{\sum }}j}\left({\displaystyle \underset{k=0}{\overset{d}{\sum }}{\pi }_{i,j,k}}\right)$.

利用排队理论中的利特尔定律，可以推导出请求节点的平均逗留时间。

3) 搭便车请求节点的平均逗留时间：

$E\left(W_1\right)=\frac{1}{{\lambda }_1}{\displaystyle \underset{i=1}{\overset{\infty }{\sum }}i\left({\displaystyle \underset{j=0}{\overset{c}{\sum }}{\displaystyle \underset{k=0}{\overset{d}{\sum }}{\pi }_{i,j,k}}}\right)}$.

4) 合作请求节点的平均逗留时间：

$E\left(W_2\right)=\frac{1}{{\lambda }_2}{\displaystyle \underset{i=0}{\overset{\infty }{\sum }}{\displaystyle \underset{j=1}{\overset{c}{\sum }}j\left({\displaystyle \underset{k=0}{\overset{d}{\sum }}{\pi }_{i,j,k}}\right)}}$.

4. 数值实验

在实际生活中，性能指标常随系统参数的变化而变化，用MATLAB进行数值分析来刻画性能指标随系统参数的变化趋势。令 $c=10,{\lambda }_1=\text{1,}{\lambda }_2=1,{\mu }_1=1,{\mu }_2=3,\epsilon =1$，图2、图3显示了休假参数θ对搭便车请求节点的平均逗留时间 $E\left(W_1\right)$ 和具有不同 $d$ 的高优先级请求节点的平均逗留时间 $E\left(W_2\right)$ 的影响，其中 $d$ 是系统允许的最大服务节点数。对于固定 $\theta$，当 $d=4$ 时，搭便车请求节点的平均逗留时间 $E\left(W_1\right)$ 和合作请求节点的平均逗留时间 $E\left(W_2\right)$ 最短。当 $d=\left\{4,5,6,7\right\}$，合作请求节点的平均逗留时间 $E\left(W_2\right)$ 随休假参数 $\theta$ 的增加而减少。由于休假参数 $\theta$ 越大，平均休假时间越短，服务节点处于服务状态的概率越高，合作请求节点的平均停留时间 $E\left(W_2\right)$ 越短。当 $d=\left\{5,6,7\right\}$ 时，搭便车请求节点的平均逗留时间 $E\left(W_1\right)$ 随着休假参数 $\theta$ 的增加而增加。当 $d=4$ 时，搭便车请求节点的平均逗留时间 $E\left(W_1\right)$ 随着休假参数 $\theta$ 的增加而减少。由于合作请求节点的抢占服务，搭便车请求节点的平均逗留时间 $E\left(W_1\right)$ 将随着休假参数 $\theta$ 的增加而减小。在不同休假参数的情况下，搭便车请求节点的平均逗留时间的数值结果如表1所示，合作请求节点的平均逗留时间的数值结果如表2所示。

Figure 2. Average sojourn time $E\left(W_1\right)$ of free riding request nodes

图2. 搭便车请求节点的平均逗留时间 $E(\; W\; 1\; )$

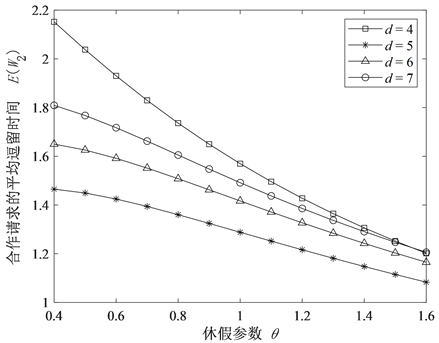
Figure 3. Average sojourn time $E\left(W_2\right)$ of cooperation request nodes

图3. 合作请求节点的平均逗留时间 $E(\; W\; 2\; )$

Table 1. Average sojourn time E ( W 1 ) of free riding request nodes

表1. 搭便车请求节点的平均逗留时间 $E(\; W\; 1\; )$

Table 2. Average sojourn time E ( W 2 ) of cooperation request nodes

表2. 合作请求节点的平均逗留时间 $E(\; W\; 2\; )$

5. 纳什均衡

本节我们将通过建立个人效益函数，来分析研究两类请求节点的均衡行为。假设搭便车请求节点和合作请求节点在系统中得到服务后的效益为 $R_1$ 和 $R_2$，在系统中单位等待时间产生的损失为 $C_1$ 和 $C_2$。搭便车请求节点和合作请求节点从进入系统开始，到服务结束为止所获得的个人效益函数为 $U_1$ 和 $U_2$，具体表达式如下：

$U_1=R_1-C_{1}E\left(W_1\right)$,

$U_2=R_2-C_{2}E\left(W_2\right)$.

假设 $c=7,d=3,{\lambda }_1={\lambda }_2=1,{\mu }_1={\mu }_2=1,\epsilon =1,R_1=R_2=50,C_1=C_2=10$，即在两类请求节点的到达率，服务率，效益和损失是相等的情况下，图4反映了两类请求节点个人效益随休假参数 $\theta$ 的变化大小。两类请求节点个人效益随着休假参数 $\theta$ 的增大而增大，这是因为随着休假参数 $\theta$ 的增大，服务节点处于异步休假的概率增大，请求节点的平均逗留时间减小，所以请求节点的个人效益增大。我们还可以看出 $U_2$ 的函数线始终在 $U_1$ 函数线的上方，无论休假参数是多少，合作请求节点的个人效益都是高于搭便车请求节点的个人效益。表3显示了 $U_1,U_2$ 具体值。

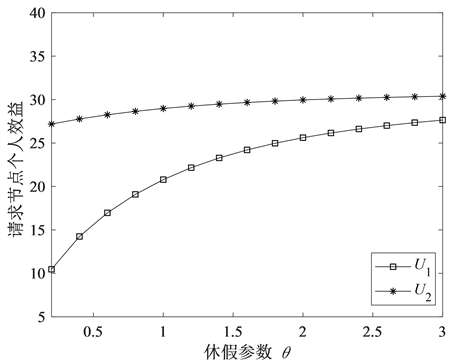
Figure 4. Request node individual benefits

图4. 请求节点个人收益

Table 3. Two types of request nodes for individual benefits

表3. 两类请求节点的个人效益值

6. 结论

本文主要针对混合P2P网络中的搭便车现象，克服其对网络不稳定的影响。提出节点优先级服务的策略，将请求节点划分成合作请求节点和搭便车请求节点。首先在M/M/c排队模型的基础上，引入负顾客、异步休假和抢占优先权等策略，构造了相应的排队模型。然后建立三维Markov链，利用拟生灭过程和矩阵几何解法得到了模型的平稳分布，进而给出系统中请求节点的平均队长、平均逗留时间和系统能耗等重要性能指标。最后利用MATLAB数值分析，描绘出参数变化对混合P2P网络系统各性能指标的影响，并通过构造个人效益函数，得到了混合P2P网络中请求节点的个人效益。结果表明合作请求节点的个人效益高于搭便车请求节点的个人效益，有效的抑制了搭便车行为，提高了对等网络的稳定性，保证了合作请求节点的服务质量。