深度学习与进化算法耦合下的最优多维随机控制问题

Solving Multi-Dimensional Optimal Stochastic Control Problems with Deep Learning and Evolution Algorithm

摘要: 受困于维数诅咒，能够求解高维偏微分方程(PDEs)的算法一直以来都极其有限。鄂维南和韩劼群在2017年提出的算法通过将未知解的梯度看作策略函数，利用深度学习可以较为有效的解决高维偏微分方程，但却无法解决带有真正策略函数的问题。本文提出了一种新算法，通过多层神经网络表示策略函数映射，将方程的解映射为适应度函数，把网络中的参数看作自变量，通过进化算法优化整个策略函数；同时配合鄂维南和韩劼群的算法求解问题。通过在Riccati方程和投资消费问题等的实际算例模拟下，表明了算法的准确性和实际意义。

Abstract: Because of the curse of dimensionality, developing efficient algorithms for solving high-dimensional partial differential equations (PDEs) has been an extremely difficult task. The algorithm which Weinan E and Jiequn Han proposed in 2017 views the gradient of the unknown solution as policy function, and through deep learning can effectively solve high-dimensional partial differential equations, but this method cannot deal with stochastic control problems with real policy function. We propose a new algorithm for solving this problem, which use multilayer neural network to represent the map of policy function and view the parameters in the neural network as independent variables. Then, we use the evolution algorithm to optimal the policy function. At the same time, we cooperate with Weinan E and Jiequn Han’s algorithm to solve this problem. Numerical results on 5-dimensional Riccati equation and 12-dimensional Investment and Consumption Problem suggest the accuracy and practical significance of the algorithm.

1. 引言

由于维数诅咒的存在 [1]，建立行之有效的高维偏微分方程(Partial differential equation, PDE)的算法一直以来都是一个非常有挑战性的工作。比较传统的求解方法是使用近似动态规划 [2]，但这种方法需要我们用一个近似函数替代掉真值函数，然后通过更新值函数的方式来求解出问题。在过去的二十多年中，由于倒向随机微分方程(Backward stochastic differential equation, BSDE)的出现及对其相关理论的充分研究，我们可以将随机偏微分方程(PDEs)的解通过Feynman-Kac公式(Feynman-Kacformula)表达为一个与其耦合的倒向随机微分方程的解 [3] [4] [5]，在这样的理论基础之上，通过蒙特卡罗方法可以建立求解随机偏微分方程(PDEs)在任意时空间位置解的算法 [6]。在信息时代的当下，鄂维南和韩劼群所开发的算法 [7] [8] [9]，是将偏微分方程和倒向随机微分方程相结合，令所求方程解的梯度充当策略函数，然后把所给定的终端条件和倒向随机微分方程的解之间的误差视为损失函数，进而通过神经网络逼近策略函数来求解出问题，这种算法在100维的非线性偏微分方程中也表现出了良好的效果。在此之后，这种通过深度学习算法来求解高维随机偏微分方程的思路应用的越来越广泛 [10] [11] [12] [13]，在误差减小、效率提升等方面的研究也获得了长足的进步 [14] [15]。

但是，鄂维南和韩劼群的算法也有一些不完备的地方，在面对带有策略函数的随机控制问题 [16] 时，这种算法就会面临整个问题出有两种策略函数需要解决的局面。考虑到鄂维南和韩劼群的算法不需要设计近似函数和处理值函数，且能够同时处理线性非线性的高维偏微分方程问题，具有较强的普适性。因此，我们仍期望从他们的算法出发，开发出能够解决含有策略函数的随机控制问题算法。

近年来，深度学习作为机器学习领域中的新技术越来越为人所知，其在机器视觉、自然语言处理和自动驾驶中的广泛应用，以及处理高维复杂问题时的优异表现让人看到了它的巨大潜能。而深度学习所具有的万能近似定理 [17] 也表明，无论是什么样的函数，我们总能够通过一个足够庞大的前馈网络来将它表示出来。这个定理的存在启发我们或许可以用深度学习的相关技术来解决我们面临的问题。

利用深度学习的知识，对于随机控制问题中的策略函数映射，我们采用多层神经网络的结构将它形式化的表达出来，而对于神经网络中本来应该通过反向传播算法进行优化的诸多参数 [18]，我们利用进化算法来进行求解。也就是说我们人为设计了一个神经网络结构表示随机控制问题的策略函数，并且通过进化算法对网络进行优化。这样的做法优点在于我们只需通过评估网络输出的结果就可以更新网络参数，而不需要像传统的神经网络算法一样，设计损失函数的形式，利用随机梯度下降算法(Stochastic gradient descent, SGD)最优化损失函数来更新参数 [17]。对于问题的余下部分，我们仍然沿用鄂维南和韩劼群的方法。

通过对有限时间指标的离散化，我们在每个时间步设置两个子网络，分别对随机控制问题的策略函数和解的梯度进行逼近。然后依据时间步的推进，将这两种类型的子网络有机的叠加在一起，形成一个非常深的网络，以此来求解我们的问题。

在本文中，我们首先对提出的算法进行了推导和架构，接着给出了整个算法的结构形式和主要部分的算法过程，并且将算法在5-Riccati方程 [19] [20] 和12-维投资消费问题 [21] 中进行了测试，结果表明算法的提出具有一定的实际意义。

2. 数值方法

我们考虑一类经典的偏微分方程(PDEs)，它具有如下的表达形式：

$\begin{array}{l}\frac{\partial u}{\partial t}\left(t,x\right)+\underset{v\in \mathcal{U}}{optimal}\{\frac{1}{2}Tr\left(\sigma \left(t,x;v\right){\sigma }^{\top }\left(t,x;v\right)\left(Hes{s}_{x}u\right)\left(t,x\right)\right)\\ +\langle \left({\nabla }_{x}u\right)\left(t,x\right),b\left(t,x;v\right)\rangle \\ \stackrel{}{}+f\left(t,x,u\left(t,x\right),{\sigma }^{\top }\left(t,x;v\right)\left({\nabla }_{x}u\right)\left(t,x\right);v\right)\}=0\end{array}$ (2.1)

其终端时刻条件为 $u\left(T,x\right)=h\left(x\right)$。

在这里，t和x表示时间和d-维的空间向量，v表示在容许控制集 $\mathcal{U}$ 上取值的m-维反馈控制过程，即问题的策略函数。此外，b为d-维向量值函数， $\sigma$ 表示 $d\times d$ 维的矩阵值函数， ${\sigma }^{\top }$ 为 $\sigma$ 的转置， $\nabla u$ 和 $Hes{s}_{x}u$ 表示函数u关于x的梯度和海森(Hessian)矩阵。

我们关心的是这个方程在 $t=0$ 时刻， $x=\xi$ 时，在最优控制 $\bar{v}\in \mathcal{U}$ 条件下的解。这里显然 $\xi \in {ℝ}^d$。

想要求解这个问题，最关键的一点是将上述的求解一个偏微分方程的问题重新表述，转化为求解一个随机控制问题。

2.1. 化偏微分方程问题(PDEs)为随机控制问题

假设 $\left(\Omega ,\mathcal{F},\mathbb{P}\right)$ 是一个概率空间， ${\left\{W_t\right\}}_{0\le t\le T}$ 是定义在这个概率空间上的d-维标准布朗运动。 ${\left\{{\mathcal{F}}_t\right\}}_{0\le t\le T}$ 是定义在 $\left(\Omega ,\mathcal{F},\mathbb{P}\right)$ 上，由布朗运动 ${\left\{W_t\right\}}_{0\le t\le T}$ 生成的自然域流； $\mathcal{A}$ 是所有具有连续轨道的 ${ℝ}^d$ -维 $\mathcal{F}$ -适应随机过程的集合。我们可以知道，反馈控制v属于集合 $\mathcal{U}$，其中 $\mathcal{U}\triangleq \left\{v|v\in {\mathcal{L}}_{\mathcal{F}}^2\left(0,T;{ℝ}^m\right)\right\}$ 在紧集 $U\in {ℝ}^m$ 上取值。

令 ${\left\{X_t\right\}}_{0\le t\le T}$ 为d-维随机过程，我们关心的随机控制问题的状态方程可以表达为：

$\{\begin{array}{l}\text{d}{X}_t^{t,\xi ;v}=b\left(t,X_t^{t,\xi ;v};v_t\right)\text{d}t+\sigma \left(t,X_t^{t,\xi ;v};v_t\right)\text{d}{W}_t\hfill \\ X_0=\xi \in {ℝ}^d\hfill \end{array}$ (2.2)

这个随机控制问题的成本函数与一个和(2.2)式耦合的倒向随机微分方程(BSDE)的解相关：

$\{\begin{array}{l}\text{d}{Y}_t^{t,\xi ;v}=-f\left(t,X^{t,\xi ;v},Y^{t,x;v},Z^{t,\xi ;v};v\right)+Z_t^{t,\xi ;v}\text{d}{W}_t\hfill \\ Y_T^{t,\xi ;v}=h\left(X_T^{t,\xi ;v}\right)\hfill \end{array}$ (2.3)

成本函数(Cost function)定义为：

$J\left(t,x;v\right)\triangleq Y_t^{t,\xi ;v}$ (2.4)

通过这个随机控制问题，我们可以找到在给定的 $\left(t,x\right)$ 和最优的反馈控制 $\bar{v}\in \mathcal{U}$ 等条件下，成本函数(2.4)的最大值或最小值。

在对f的合理假设下，我们可以发现对于所有的 $t\in \left(0,T\right)$，偏微分方程(PDEs) (2.1)和倒向随机微分方程(BSDEs) (2.3)存在如下的关系 [3] [4] [5]：

$Y_t^{t,\xi ;v}=u\left(t,X_t^{t,\xi ;v}\right)\in ℝ,Z_t^{t,\xi ;v}={\sigma }^{\top }\left(t,X_t^{t,\xi ;v};v\right)\left({\nabla }_{x}u\right)\left(t,X_t^{t,\xi ;v}\right)\in {ℝ}^d$ (2.5)

(2.5)中的左式通常被称作为非线性的Feynman-Kac公式。

通过上述变换，我们将求解偏微分方程(PDEs) (2.1)的问题转化为求解一个与之相匹配的随机控制问题(2.2)~(2.4)。从而，通过求解随机控制问题(2.2)~(2.4)，我们可以利用 $J\left(0,\xi \right)$ 来计算出(2.1)式在最优反馈控制 $\bar{v}$ 下的值 $u\left(0,\xi \right)$。

我们通过两个简短的步骤来说明求解 $u\left(0,\xi \right)$ 的数值算法：

1) 在反馈控制 $v\in \mathcal{U}$ 中，选定一条样本轨道 $\hat{v}$，我们可以得到与之相对应的随机控制问题的解 $J\left(0,\xi ;\hat{v}\right)$。并且，对于不同的样本轨道 $\hat{v}$，我们总能够得到与之相对应的 $J\left(0,\xi ;\hat{v}\right)$。因此，通过对反馈控制v的充分采样，我们能够得到充分多的 $\hat{v}-J$ 对。

2) 对于1中的所有 $\hat{v}-J$ 对，我们能够找到一个反馈控制 $\bar{v}\in \hat{v}$，使得 $J\left(0,\xi \right)$ 达到最大值或者最小值。

在下一章节中，我们首先讨论第1步的具体实施方法。

2.2. 偏微分方程(PDEs)的神经网络算法

为了推导出求解 $J\left(0,\xi ;\cdot \right)$ 的数值算法，我们假设在(2.2)~(2.4)中选取了反馈控制v的一条轨道 $\hat{v}$，并将(2.5)中的两个公式插入到(2.3)中，我们可以得到对于所有的 $t\in \left[0,T\right]$ ：

随机控制问题的状态方程改写为：

$X_t=\xi +{\displaystyle {\int }_0^{t}b}\left(s,X_s;{\hat{v}}_s\right)\text{d}s+{\displaystyle {\int }_0^t\sigma }\left(s,X_s;{\hat{v}}_s\right)\text{d}{W}_s$ (2.6)

与状态方程相耦合的倒向随机微分方程(BSDE)便为：

$\begin{array}{l}u\left(t,X_t\right)=h\left(X_T\right)+{\displaystyle {\int }_t^{T}f}\left(s,X_s,u\left(s,X_s\right),{\sigma }^{\top }\left(s,X_s;{\hat{v}}_s\right)\left({\nabla }_{x}u\right)\left(s,X_s\right);{\hat{v}}_s\right)\text{d}s\\ -{\displaystyle {\int }_t^T\langle {\sigma }^{\top }\left(s,X_s;{\hat{v}}_s\right)\left({\nabla }_{x}u\right)\left(s,X_s\right),\text{d}{W}_s\rangle }\end{array}$ (2.7)

成本函数为：

$J\left(t,x;\hat{v}\right)\triangleq u\left(t,X_t^{t,\xi ;\hat{v}}\right)$ (2.8)

我们将 $u\left(0,\xi \right)\approx {\theta }_{u0}$， $\left({\nabla }_{x}u\right)\left(0,\xi \right)\approx {\theta }_{\nabla u0}$ 视为模型的参数，然后对(2.6)，(2.7)式采取时间离散化。

具体来说，令 $t_0,t_1,\cdots ,t_N\in \left[0,T\right],N\in \mathbb{N}$，其满足：

$0=t_0<t_1<\cdots <t_N=T$ (2.9)

当 $N\in \mathbb{N}$ 充分大时，对(2.6)、(2.7)式，我们考虑一种简单的欧拉格式(Euler scheme)：

对于 $n=1,\cdots ,N-1$，我们能够得到

$X_{t_{n+1}}-X_{t_n}\approx b\left(t_n,X_{t_n};{\hat{v}}_{t_n}\right)\Delta t_n+\sigma \left(t_n,X_{t_n};{\hat{v}}_{t_n}\right)\Delta W_n$ (2.10)

和

$\begin{array}{l}u\left(t_{n+1},X_{t_{n+1}}\right)-u\left(t_n,X_n\right)\\ \approx -f\left(t_n,X_{t_n},u\left(t_n,X_{t_n}\right),{\sigma }^{\top }\left(t_n,X_{t_n}\right)\left({\nabla }_{x}u\right)\left(t_n,X_{t_n}\right);{\hat{v}}_{t_n}\right)\Delta t_n\\ +\langle {\sigma }^{\top }\left(t_n,X_{t_n};{\hat{v}}_{t_n}\right)\left({\nabla }_{x}u\right)\left(t_n,X_{t_n}\right),\Delta W_n\rangle \end{array}$ (2.11)

其中

$\Delta t_n=t_{n+1}-t_n,\Delta W_n=W_{t_{n+1}}-W_{t_n}$ (2.12)

在这样的时间离散化下，可以轻易地通过式(2.10)来采样获得轨道 ${\left\{X_{t_n}\right\}}_{0\le n\le N}$。

我们通过在每个时间步 $t=t_n$ 使用多层反馈神经网络数值算法来逼近函数 $x\mapsto {\sigma }^{\top }\left(t,x\right)\left({\nabla }_{x}u\right)\left(t,x\right)$ 的值 [9]：

${\sigma }^{\top }\left(t_n,X_{t_n}\right)\left({\nabla }_{x}u\right)\left(t_n,X_{t_n}\right)\approx \left({\sigma }^{\top }{\nabla }_{x}u\right)\left(t_n,X_{t_n}|{\theta }_n\right)$ (2.13)

其中 ${\theta }_n$ 表示网络在 $n=1,\cdots ,N-1$ 时的参数。

如果已知 ${\theta }_{u0}$ 的值，那么我们就可以近似地求解出(2.13)的值，然后将其代入(2.11)，再对(2.11)进行递归计算来求解出 $u\left(t_n,X_{t_n}\right),n\in \left\{1,\cdots ,N\right\}$ 的值。

具体来说，这个方法是将轨道 ${\left\{X_{t_n}\right\}}_{0\le n\le N}$ 和标准布朗运动 ${\left\{W_{t_n}\right\}}_{0\le n\le N}$ 作为模型的输入数据，而 $\hat{u}\left(X_{t_n},W_{t_n}\right),n\in \left[0,N\right]$ 则视为模型输出，它是 $u\left(t,X_t\right)$ 的近似解。

我们使用均方误差损失函数(Mean squared error, MSE)来衡量给定的终端条件 $h\left(X_{t_N}\right)$ 和计算出来的近似值 $\hat{u}\left(X_{t_N},W_{t_N}\right)$ 之间的差距 [18]：

$L\left(\theta \right)=\mathbb{E}\left[{\left|h\left(X_{t_N}\right)-\hat{u}\left(X_{t_N},W_{t_N}\right)\right|}^2\right]$ (2.14)

整个网络的参数为 $\theta =\left\{{\theta }_{u0},{\theta }_{\nabla u0},{\theta }_1,\cdots ,{\theta }_{N-1}\right\}$。

现在，我们可以使用随机梯度下降算法(SGD)，通过优化参数集 $\theta$ 来最小化均方误差损失函数(MSE)。对于使得均方误差损失函数(MSE)达到最小的参数集 $\theta$，其中 ${\theta }_{u0}\in \theta$ 是对 $u\left(0,\xi \right)$ 的近似，而 $u\left(0,\xi \right)$ 就是我们想要的 $J\left(0,\xi ;\hat{v}\right)$ 的值，这里的 $\hat{v}$ 是我们对反馈控制v采样获得的一条轨道。因此我们就获得了一个 $\hat{v}-J$ 对。

我们使用伪代码的形式简略的呈现一下这个计算过程：

在下一章中，我们讨论第2步的做法。

2.3. 反馈控制函数的进化算法

在2.2节中，对于反馈控制v采样获得的轨道 $\hat{v}$，我们可以获得与之对应的 $J\left(0,\xi ;\hat{v}\right)$，即 $\hat{v}-J$ 对。在这个章节中，我们会推导出一个数值算法，通过优化 $\hat{v}$ 来获得我们想要的最优解 $J\left(0,\xi \right)$。

我们可以将问题变形为：

$V=\underset{\hat{v}}{optimal}J\left(0,\xi ;\hat{v}\right)$ (2.15)

其中 $V\in ℝ$ 就是我们的优化目标。我们将 $\hat{v}\in {ℝ}^m$ 视为方程的自变量，这个问题就可以看作是单目标优化问题(Single-Objective Optimization Problem)。

通常来说，在单目标优化问题中，可以利用进化算法(Evolution algorithm, EA)将自变量编码为种群，将目标函数映射为适应度函数，由此获得种群中每个个体相对应的适应度，接着以适应度为标准，通过若干代的变异、交叉和选择，算法可以得到最优的适应度，从而得到最优的目标函数值 [22] [23]。

然而，在我们的问题中，自变量 $\hat{v}$ 并非数字而是一个随机过程。在这种情况下，我们不能简单的把 $\hat{v}$ 像数值一样进行编码来进行优化求解。

我们沿用2.1节中的假设条件，令 $t\in \left[0,T\right]$， $X_t\in {ℝ}^d$ (见(2.6)式)。反馈控制v的表达式我们定义为：

$v:=v\left(t,X_t\right)$ (2.16)

其由 ${ℝ}^m$ 维均方可积 ${\left\{{\mathcal{F}}_t\right\}}_{0\le t\le T}$ -适应过程组成。

我们将时间离散化方法(2.9)应用于(2.16)，则随机过程可被离散化为：

$v_{t_n}:=v\left(t_n,X_{t_n}\right)$ (2.17)

其中 $n=0,\cdots ,N-1$， $X_{t_n}$ 的值可以由(2.10)得到。

假设映射 $x\mapsto v\left(t,x\right)$ 已经给定，那么我们可以很轻松地通过 $t_{n_{}}$ 和 $X_{t_n}$ 计算出的 $v\left(t_n,X_{t_n}\right)$ 值。

然而，大多数的情况下我们并不知道映射 $x\mapsto v\left(t,x\right)$ 的形式，所以，我们需要找到一个方法表达出这个映射。

作为一种新兴的技术，深度神经网络模型在人工智能领域具有广泛的应用，并且它可以通过将简单函数进行复合来表达非常复杂的函数方程，所以，我们可以利用神经网络模型的这种性质来表达出映射 $x\mapsto v\left(t,x\right)$。

首先，对于任意的 $n=0,\cdots ,N-1$ 和 $X_{t_n}$，我们有：

$v^{\prime }\left(X_{t_n}\right)\approx f_n^{\left(M\right)}\left(f_n^{\left(M-1\right)}\left(\cdots \left(f_n^{\left(2\right)}\left(f_n^{\left(1\right)}\left(X_{t_n}\right)\right)\right)\right)\right)$ (2.18)

这里的M表示多层神经网络的层数， $f_n^{\left(m\right)}$ 则表示从第 $m-1$ 层到第m层的映射，其中 $m=1,\cdots ,M$。需要注意的是， $m=0$ 时表示输入层 [17] [18]。

当 $m=1,\cdots ,M-1$ 时，假设 $h_n^{m-1}\in {ℝ}^{{\rho }_n^m}$ 和 $h_n^m\in {ℝ}^{k_n^m}$ 分别是函数 $f_n^{\left(m\right)}$ 的自变量和因变量，那么 $f_n^{\left(m\right)}$ 的表达式可以定义为：

$h_n^m=g\left(K_n^{m,\top }{h}_n^{m-1}+b_n^m\right)$ (2.19)

这里的权重矩阵 $K_n^m\in {ℝ}^{{\rho }_n^m\times k_n^m}$ 和偏置 $b_n^m\in {ℝ}^{k_n^m}$ 均为函数的参数。其中 $g(\cdot )$ 为激活函数，它能够对输入的自变量中的每个元素按照给定的规则产生作用 [18]。并且，在(2.19)中得到的 $h_n^m$ 会作为下一层函数 $f_n^{\left(m+1\right)}$ 的自变量传递下去。

需要注意的是输出层函数 $f_n^{\left(M\right)}$ 不需要使用激活函数。

为了方便记录，我们用 ${\varphi }_n^m$ 表示函数 $f_n^{\left(m\right)}$ 的参数 $\left(K_n^m,b_n^m\right)$，因此，在 $t=t_n$ 时刻时(2.18)式的全部参数为 ${\varphi }_n=\left\{{\varphi }_n^1,\cdots ,{\varphi }_n^M\right\}$。

因此，当 $n=0,\cdots ,N-1$ 和 $X_{t_n}$ 时，我们可以将式改写为：

$v^{\prime }\left(X_{t_n}\right)=K_n^{M,\top }g\left(g\left(\cdots g\left(g\left(X_{t_n};{\varphi }_n^{\left(1\right)}\right);{\varphi }_n^{\left(2\right)}\right);{\varphi }_n^{\left(M-2\right)}\right);{\varphi }_n^{\left(M-1\right)}\right)+b_n^M$ (2.20)

其参数为 ${\varphi }_n=\left\{{\varphi }_n^1,\cdots ,{\varphi }_n^M\right\}$。

同样的，为了方便记录，我们把(2.20)式缩写为 $v^{\prime }\left(X_{t_n}\right)=f_n\left(X_{t_n};{\varphi }_n\right)$， $t=t_n$。

显然，这个网络以 $X_{t_n}$ 作为输入数据，并且以 $v^{\prime }\left(X_{t_n}\right)$ 作为输出数据，而 $v^{\prime }\left(X_{t_n}\right)$ 则是 $v\left(t_n,X_{t_n}\right)$ 的一个近似。在这里我们指出，我们得到的 $v^{\prime }$ 就是2.2节中我们采样获得的轨道 $\hat{v}$。

由此可知，当 $n\in \left\{0,\cdots ,N-1\right\}$ 时， $v\left(t_n,X_{t_n};\Phi \right)\in {ℝ}^m$ 的值可以由(2.20)式和(2.10)式联合起来递归地计算得出，其中 $\Phi =\left\{{\varphi }_0,\cdots ,{\varphi }_{N-1}\right\}$ 表示函数v的全体参数。因此，(2.15)式的自变量就可以看成是 $\Phi$，我们的优化问题就变形为： $V=\underset{\Phi }{optimal}J\left(0,\xi ;\hat{v}\left(X;\Phi \right)\right)$。

现在我们就可以使用进化算法 [23] [24] (EA)通过 $\Phi$ 来优化V的值，就像使用进化算法来解决一个经典的单目标优化问题一样。

我们同样的使用伪代码的形式简略的呈现一下这个计算过程

3. 偏微分方程和随机控制的数值算例

在本节当中，我们通过几个具有实际意义的偏微分方程(PDEs)算例来说明第二章2.2节和2.3节推导出的算法。在接下来的例子之中，我们会对2.2节中的近似计算使用小批量(mini-batches)样本的Adam优化器 [17] [18]，对2.3节中V的优化我们采用一种改进的进化算法来进行计算 [24]。

如图1，在我们的实践过程中，对于2.3节，我们采用N个全连接反馈神经网络的结构形式来表示 ${\hat{v}}_n^{\Phi }$，其中 $\Phi =\left\{{\varphi }_0,\cdots ,{\varphi }_{N-1}\right\},n\in \left\{0,1,\cdots ,N-1\right\}$。每一个网络都表示在 $t=t_n$ 时刻 $X_{t_n}\mapsto {\hat{v}}_n$ 的映射，它包括一个输入层(d-维)，H个隐藏层(具有相同的维数)以及一个输出层(m维)。这些网络的所有权重都服从均匀分布。此外，我们利用 $N-1$ 个多层神经网络来计算 $\left({\sigma }^{\top }{\nabla }_{x}u\right)\left(t_n,X_{t_n}|{\theta }_n\right),n\in \left\{1,2,\cdots ,N-1\right\}$，其中 ${\theta }_n$ 表示神经网络在 $t=t_n$ 时刻的参数 [8]，在这里，神经网络的参数通过正态分布或者均匀分布完成初始化。整个网络结构有 $\left(D+1\right)\left(N-1\right)+\left(H+1\right)N$ 层的若干参数需要优化。

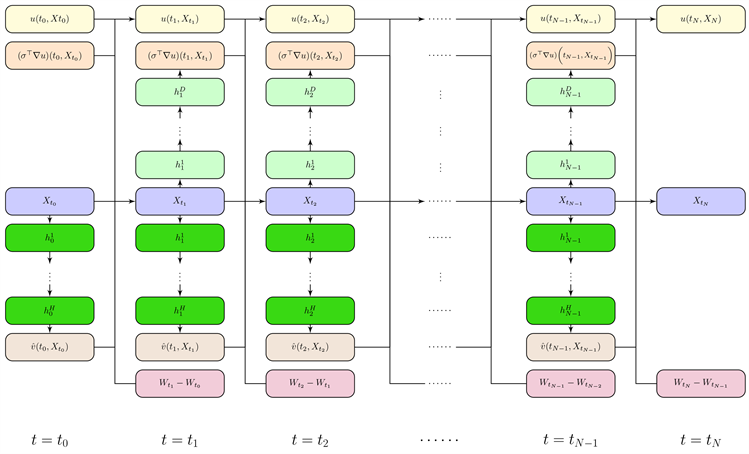
Figure 1. Numerical algorithm structure of stochastic control problems

图1. 随机控制问题的数值算法结构图

3.1. 倒向随机Riccati方程

在本节当中，我们将推导出来的算法应用在倒向随机Riccati方程 [19] [20] 中来测试它的数值效果。

令 $t\in \left[0,T\right]$， $x,W\in {ℝ}^d$， $v\in {ℝ}^m$， $u\in ℝ$， $z\in {ℝ}^{1\times d}$。当 $d=2$， $m=1$，， $\xi =\left(1,\cdots ,1\right)$ 时，有(2.2)式中

$b\left(t,x_t;v_t\right)=\left(A{x}_t+B{v}_t\right)=\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right)x_t+\left(\begin{array}{c}0.1\\ 0.1\end{array}\right)v_t$ (3.1)

$\begin{array}{c}\sigma \left(t,x_t;v_t\right)\text{d}{W}_t={\displaystyle \underset{i=1}{\overset{d}{\sum }}\left(C^i{x}_t+D^i{v}_t\right)\text{d}{W}_t^i}\\ =\left[\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right)x_t+\left(\begin{array}{c}0\\ 0.1\end{array}\right)v_t\right]\text{d}{W}_t^1\\ +\left[\left(\begin{array}{cc}0.1& 0\\ 0& 0\end{array}\right)x_t+\left(\begin{array}{c}0.1\\ 0\end{array}\right)v_t\right]\text{d}{W}_t^2\end{array}$ (3.2)

同样地，在(2.3)式中

$f\left(t,x,u,z;v\right)=\left(\langle Q{x}_t,x_t\rangle +\langle N{x}_t,x_t\rangle \right)=x_t^{\top }\left(\begin{array}{cc}0.5& 0\\ 0& 0.3\end{array}\right)x_t+0.1v_t^{\top }{v}_t$ (3.3)

并且它的终端时刻条件我们定义为 $h\left(x\right)=\langle Mx,x\rangle =x^{\top }\left(\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right)x$。

此时，当 $t\in \left[0,T\right]$， $x\in {ℝ}^d$，使得 $u\left(T,x\right)=h\left(x\right)$ 时，偏微分方程(PDEs) (2.1)的解u满足：

$\begin{array}{l}\frac{\partial u}{\partial t}\left(t,x\right)+\underset{v}{\inf }\{\frac{1}{2}{\displaystyle \underset{\alpha ,\beta }{\sum }{\displaystyle \underset{i=1}{\overset{d}{\sum }}\left(C_{\alpha }^{i}x+D_{\alpha }^i{v}_t\right)}}\left(C_{\beta }^{i}x+D_{\beta }^i{v}_t\right)\left(D_{\alpha ,\beta }u\right)\left(t,x\right)\\ +{\displaystyle \underset{\gamma }{\sum }\left(A_{\gamma }x+B_{\gamma }{v}_t\right)}\left(D_{\gamma }u\right)\left(t,x\right)+x^{\top }Qx+v_t^{\top }N{v}_t\}=0\end{array}$ (3.4)

Table 1. Numerical simulation of 2-dimensional Riccati equation

表1. Riccati方程在2-维形势下的数值模拟

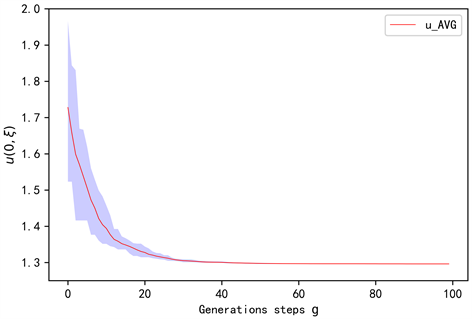
Figure 2. Solution of 2-dimensional Riccati equation against generations steps g

图2. 2-维Riccati方程的解随进化代数g的变化

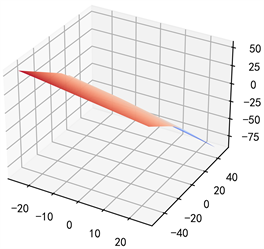
Figure 3. Value of function $f_n\left(x;{\varphi }_n\right)$ against x, where $n\in \left\{0,1,\cdots ,N-1\right\}$

图3. 函数 $f_n\left(x;{\varphi }_n\right)$ 随x的变化，其中 $n\in \left\{0,1,\cdots ,N-1\right\}$

在表1中，我们令进化算法的进化代数为100代，每一代的种群规模 $NP=20$。在进化过程中，我们计算了每一代的最优 $u\left(0,\xi \right)$ 值，相应规模下 $u\left(0,\xi \right)$ 的均值及标准差。图2为2-维Riccati方程的解 $u\left(t=0,\xi =\left(1,1\right)\right)$ 在20个等距时间步的离散下随进化代数g的变化情况。图中的阴影部分表示每一代种群中 $\max u\left(0,\xi \right)$ 和 $\min u\left(0,\xi \right)$ 之间的差值。红色的线表示 $u\left(0,\xi \right)$ 的均值。在100代9541.29秒的进化后，该数值方法获得的解的标准差为2.87E−04。图3为函数 $f_n\left(x;{\varphi }_n\right)$， $n\in \left\{0,1,\cdots ,N-1\right\}$，其中 ${\varphi }_n$ 为参数，由我们在2.2节、2.3节推导出的算法求解得出，此时， $x\in {ℝ}^2$， $x_1\in \left\{-20,\cdots ,20\right\},x_2\in \left\{-40,\cdots ,40\right\}$。

在图2关于 $u\left(0,\xi \right)$ 的计算中，由我们推导出的算法可知，此时偏微分方程(3.4)的真实解可由1.29581代替。

此外，u还可以通过 $u_t=x_t^{\top }{K}_t{x}_t$ 来计算获得 [20]，其中 $K_t$ 的值可以通过下列方程组配合倒向欧拉算法 [27] (Backward Euler method)解出来

$\{\begin{array}{l}\text{d}{K}_t=A^{\top }{K}_t+K_{t}A+Q+{\displaystyle \underset{i=1}{\overset{d}{\sum }}{\left(C^i\right)}^{\top }}{K}_t{D}^i\\ -\left[K_{t}B+\underset{i=1}{\overset{d}{{\displaystyle \sum }}}{\left(C^i\right)}^{\top }{K}_t{D}^i\right]{\left[N+{\displaystyle \underset{i=1}{\overset{d}{\sum }}{\left(D^i\right)}^{\top }}{K}_t{D}^i\right]}^{-1}{\left[K_{t}B+{\displaystyle \underset{i=1}{\overset{d}{\sum }}{\left(C^i\right)}^{\top }}{K}_t{D}^i\right]}^{\top }\\ K_T=M\end{array}$ (3.5)

在这种方法下，我们有 $u\left(0,\xi \right)=1.29538$，这与我们所推导出来的算法之间的误差大小为0.00043。

更进一步，我们考虑当 $d=5$， $m=5$， $\xi =\left(1,\cdots ,1\right)$ 时的情况，令(2.2)式中 $b_t$ 为：

$b\left(t,x_t;v_t\right)=\left(A{x}_t+B{v}_t\right)=\left(\begin{array}{ccccc}0.1& 0& 0& 0& 0\\ 0& 0.1& 0& 0& 0\\ 0& 0& 0.3& 0& 0\\ 0& 0& 0& 0.1& 0\\ 0& 0& 0& 0& 0.1\end{array}\right)x_t+\left(\begin{array}{ccccc}0.1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)v_t$ (3.6)

${\sigma }_t$ 见后文附录。

此时，有(2.3)中函数f为：

$\begin{array}{c}f\left(t,x,u,z,v\right)=\left(\langle Q{x}_t,x_t\rangle +\langle N{x}_t,x_t\rangle \right)\\ =x_t^{\top }\left(\begin{array}{ccccc}0.01& 0& 0& 0& 0\\ 0& 0.1& 0& 0& 0\\ 0& 0& 0.02& 0& 0\\ 0& 0& 0& 0.1& 0\\ 0& 0& 0& 0& 0.02\end{array}\right)x_t+v_t^{\top }\left(\begin{array}{ccccc}0.01& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0.01& 0\\ 0& 0& 0& 0& 0\end{array}\right)v_t\end{array}$ (3.7)

相应地，终端时刻条件为 $h\left(x\right)=\langle Mx,x\rangle =x^{\top }\left(\begin{array}{ccccc}0.02& 0& 0& 0& 0\\ 0& 0.12& 0& 0& 0\\ 0& 0& 0.12& 0& 0\\ 0& 0& 0& 0.2& 0\\ 0& 0& 0& 0& 0.2\end{array}\right)x$。

在表2中，我们令进化算法的进化代数为150代，每一代的种群规模 $NP=30$。在进化过程中，我们计算了每一代的最优 $u\left(0,\xi \right)$ 值，相应规模下 $u\left(0,\xi \right)$ 的均值及标准差。图4为5-维Riccati方程的解 $u\left(t=0,\xi =\left(1,\cdots ,1\right)\right)$ 在20个等距时间步的离散下随进化代数g的变化情况。图中的阴影部分表示每一代种群中 $\max u\left(0,\xi \right)$ 和 $\min u\left(0,\xi \right)$ 之间的差值。红色的线表示 $u\left(0,\xi \right)$ 的均值。在150代24699.45秒的进化后，该数值方法获得的解的标准差为1.01E−03。图5为函数 $f_n\left(x;{\varphi }_n\right)$， $n\in \left\{0,1,\cdots ,N-1\right\}$，其中 ${\varphi }_n$ 为参数，由我们在2.2节、2.3节推导出的算法求解得出，此时， $x\in {ℝ}^5$， $x_1\in \left\{-20,\cdots ,20\right\},x_2\in \left\{-40,\cdots ,40\right\}$， $x_3,x_4,x_5\in \left\{1,\cdots ,1\right\}$。

Table 2. Numerical simulation of 5-dimensional Riccati equation

表2. Riccati方程在5-维形势下的数值模拟

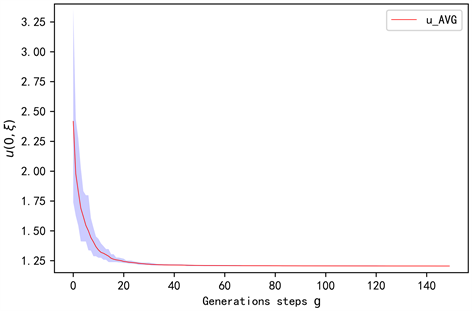
Figure 4. Solution of 5-dimensional Riccati equation against generations steps g

图4. 5-维Riccati方程的解随进化代数g的变化

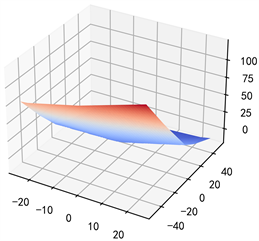
Figure 5. Value of function $f_n\left(x;{\varphi }_n\right)$ against x, where $n\in \left\{0,1,\cdots ,N-1\right\}$

图5. 函数 $f_n\left(x;{\varphi }_n\right)$ 随x的变化，其中 $n\in \left\{0,1,\cdots ,N-1\right\}$

在图4关于5-维Riccati方程的解 $u\left(0,\xi \right)$ 的计算中，我们用1.20332来代替它真实值。此时，利用 $u_t=x_t^{\top }{K}_t{x}_t$ 和 式可以得出 $u\left(0,\xi \right)$ 值为1.19665，两种算法之间的误差为0.00667。

3.2. 基于CIR模型和随机波动率的最优投资消费问题

在这一节当中，我们将算法应用在投资消费问题中。此时，将问题放在一个没有税收和交易成本，但具有CIR利率 [28] 和随机波动率的金融市场中 [21]。

需要注意的是的在这个问题当中，偏微分方程(2.1)的反馈控制过程v将不再只是一个，而是由一对随机过程来担任，我们用 $\left(\pi ,C\right)$ 来表示 [21]，其中 $\pi$ 表示股票投资额，C表示消费利率。

一般的，有 $t\in \left[0,T\right]$， $x\in {ℝ}^d$， $W\in {ℝ}^{2d}$， $\pi ,C\in {ℝ}^m$， $r,\eta \in {ℝ}^d$， $u\in ℝ$， $z\in {ℝ}^{1\times d}$，此时，我们令 $T=1$， $d=1$， $m=1$， $\xi =30$，则在中(2.2)有

$b\left(t,r_t,{\eta }_t,x_t;{\pi }_t,c_t\right)=r_t{x}_t+{\pi }_{t}k{\eta }_t-c_t=r_t{x}_t+0.6{\pi }_t{\eta }_t-c_t$ (3.8)

$\sigma \left(t,{\eta }_t,x_t;{\pi }_t\right)\text{d}{W}_t^2={\pi }_t{\sigma }_1\sqrt{{\eta }_t}\text{d}{W}_t^2=1.2{\pi }_t\sqrt{{\eta }_t}\text{d}{W}_t^2$ (3.9)

同时，r， $\eta$ 都是随机过程，且它们的形式由CIR模型给出

$\{\begin{array}{l}\text{d}{r}_t=\left(0.25-0.15r_t\right)\text{d}t+0.2\sqrt{r_t}\text{d}{W}_t^1\hfill \\ r\left(0\right)=0.05\in {ℝ}^d\hfill \end{array}$ (3.10)

$\{\begin{array}{l}\text{d}{\eta }_t=\left(0.85-0.6{\eta }_t\right)\text{d}t+0.25\sqrt{{\eta }_t}\text{d}{W}_t^2\hfill \\ \eta \left(0\right)=0.36\in {ℝ}^d\hfill \end{array}$ (3.11)

在(2.3)式中，我们有 $f\left(t,x,u,z;c\right)=\alpha \frac{c_t^{\delta }}{\delta }{\text{e}}^{-\beta t}=0.4\frac{c_t^{0.1}}{0.1}{\text{e}}^{-0.1t}$，并且此时的终端时刻条件为 $h\left(x\right)=\left(1-\alpha \right)\frac{x_T^{\delta }}{\delta }{\text{e}}^{-\beta T}=0.6\frac{x_T^{0.1}}{0.1}{\text{e}}^{-0.1T}$。

在这种规定之下，我们可知偏微分方程(2.1)在 $t\in \left[0,T\right]$， $x\in {ℝ}^d$ 时的解u满足：

$\begin{array}{l}\frac{\partial u}{\partial t}+\underset{\pi ,C}{\max }\{\left(r_{t}x+{\pi }_{t}k{\eta }_t-C_t\right)\left(D_{x}u\right)+\frac{1}{2}{\pi }_t^2{\sigma }_1^2{\eta }_t\left(D_x^{2}u\right)+\left(\theta -C_t{r}_t\right)\left(D_{r}u\right)\\ +\frac{1}{2}{\sigma }_0^2{r}_t\left(D_r^{2}u\right)+\left(b-a{\eta }_t\right)\left(D_{\eta }u\right)+\frac{1}{2}{\sigma }_2^2{\eta }_t\left(D_{\eta }^{2}u\right)+{\pi }_t{\sigma }_1{\sigma }_2\left(D_{x\eta }u\right)+\alpha {\text{e}}^{-\beta t}\frac{C_t^{\delta }}{\delta }\}=0\end{array}$ (3.12)

Table 3. Numerical simulation of 3-dimensional Investment and Consumption problem

表3. 投资消费问题在3-维形式下的数值模拟

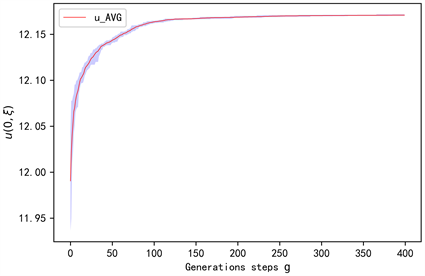
Figure 6. Solution of 3-dimensional Investment and Consumption problem against generations steps g

图6. 3-维投资消费问题的解随进化代数g的变化

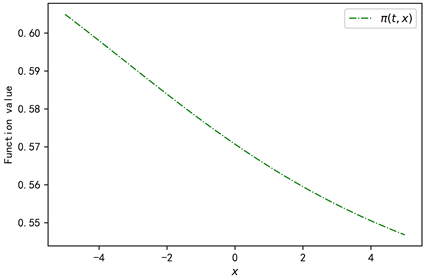
Figure 7. Value of function $f_{n,\pi }\left(x;{\varphi }_{n,\pi }\right)$ against x, where $n\in \left\{0,1,\cdots ,N-1\right\}$

图7. 函数 $f_{n,\pi }\left(x;{\varphi }_{n,\pi }\right)$ 随x的变化，其中 $n\in \left\{0,1,\cdots ,N-1\right\}$

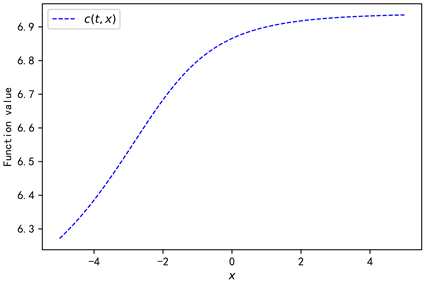
Figure 8. Value of function $f_{n,C}\left(x;{\varphi }_{n,C}\right)$ against x, where $n\in \left\{0,1,\cdots ,N-1\right\}$

图8. 函数 $f_{n,C}\left(x;{\varphi }_{n,C}\right)$ 随x的变化，其中 $n\in \left\{0,1,\cdots ,N-1\right\}$

在表3中，我们令进化算法的进化代数为400代，每一代的种群规模 $NP=30$。在进化过程中，我们计算了每一代的最优 $u\left(0,\xi \right)$ 值，相应规模下 $u\left(0,\xi \right)$ 的均值及标准差。图6为3-维投资消费问题(3.12)的解 $u\left(t=0,\xi =30\right)$ 在20个等距时间步的离散下随进化代数g的变化情况。图中的阴影部分表示每一代种群中 $\max u\left(0,\xi \right)$ 和 $\min u\left(0,\xi \right)$ 之间的差值。红色的线表示 $u\left(0,\xi \right)$ 的均值。在400代40660.70秒的进化后，该数值方法获得的解的标准差为3.17596E−04。图7为函数 $f_{n,\pi }\left(x;{\varphi }_{n,\pi }\right)$， $n\in \left\{0,1,\cdots ,N-1\right\}$，其中 ${\varphi }_{n,\pi }$ 为映射 $x_{t_n}\mapsto \pi \left(t_n,x_{t_n}\right)$ 中的参数，由我们在2.2节、2.3节推导出的算法求解得出，自变量 $x\in \left\{-5,\cdots ,5\right\}\in ℝ$ ；同样的，图8为函数 $f_{n,C}\left(x;{\varphi }_{n,C}\right)$。

在图6关于 $u\left(0,\xi \right)$ 的计算中，我们有偏微分方程(3.12)在 $t=0$， $r\left(0\right)=0.05$， $\eta \left(0\right)=0.36$， $\xi =30$ 真实解可由12.1718代替。

更进一步，我们考虑当 $\eta \in {ℝ}^{10}$， $W\in {ℝ}^{11}$ 时的情况。此时令 $\xi =25$，则有(2.2)中

$b\left(t,r_t,{\eta }_t,x_t;{\pi }_t,c_t\right)=r_t{x}_t+{\pi }_t\langle k,{\eta }_t\rangle -c_t$ (3.13)

$\sigma \left(t,{\eta }_t,x_t;{\pi }_t\right)\text{d}{W}_t={\pi }_t{\displaystyle \underset{i=1}{\overset{10}{\sum }}{\sigma }_1}\sqrt{{\eta }_t^i}\text{d}{W}_t^i$ (3.14)

这里我们令 $k=\left(\begin{array}{c}0.6\\ 0.55\\ 0.5\\ 0.48\\ 0.58\\ 0.62\\ 0.4\\ 0.62\\ 0.52\\ 0.75\end{array}\right)$， ${\sigma }_1=\left(\begin{array}{c}0.45\\ 0.62\\ 0.75\\ 0.5\\ 0.82\\ 0.64\\ 1.0\\ 0.82\\ 0.64\\ 0.8\end{array}\right)$。

此时，由于随机过程 ${\left\{{\eta }_t\right\}}_{0\le t\le T}$ 为10-维，所以它的形式变为

$\{\begin{array}{l}\text{d}{\eta }_t^1=\left(b^1-a^1{\eta }_t^1\right)\text{d}t+{\sigma }_2^1\sqrt{{\eta }_t^1}\text{d}{W}_t^1\hfill \\ ⋮\hfill \\ \text{d}{\eta }_t^{10}=\left(b^{10}-a^{10}{\eta }_t^{10}\right)\text{d}t+{\sigma }_2^{10}\sqrt{{\eta }_t^{10}}\text{d}{W}_t^{10}\hfill \\ \eta \left(0\right)={\eta }_0\in {ℝ}^{10}\hfill \end{array}$ (3.15)

这个时候方程的初始时刻条件 ${\eta }_0$ 我们定义为 ${\eta }_0=\left(\begin{array}{c}0.13\\ 0.25\\ 0.32\\ 0.37\\ 0.18\\ 0.42\\ 0.2\\ 0.15\\ 0.1\\ 0.12\end{array}\right)$。需要指出的是，此时方程中的参数均为向量形式，其具体形式为 $b=\left(\begin{array}{c}0.72\\ 0.78\\ 0.58\\ 0.75\\ 0.8\\ 0.58\\ 0.55\\ 0.65\\ 0.62\\ 0.58\end{array}\right)$， $a=\left(\begin{array}{c}0.18\\ 0.22\\ 0.32\\ 0.18\\ 0.28\\ 0.3\\ 0.2\\ 0.17\\ 0.18\\ 0.24\end{array}\right)$， ${\sigma }_2=\left(\begin{array}{c}0.13\\ 0.25\\ 0.12\\ 0.14\\ 0.22\\ 0.16\\ 0.14\\ 0.32\\ 0.15\\ 0.12\end{array}\right)$。而 $b^1\cdots b^{10}$， $a^1\cdots a^{10}$， ${\sigma }_2^1\cdots {\sigma }_2^{10}$ 则为对应向量的相应分量。

需要指出的是，这时(3.13)，(3.14)，(3.15)式中的参数k， ${\sigma }_1$，b，a， ${\sigma }_2$ 及 ${\left\{{\eta }_t\right\}}_{0\le t\le T}$ 的初始时刻条件 ${\eta }_0$ 均为向量，我们在附录中给出它们的具体值。在这样的设定下，我们令(2.3)式函数f的参数 $\alpha =0.3$， $\delta =0.08$，并且保持其它的所有参数按照3-维情况下给出的各个值保持不变。

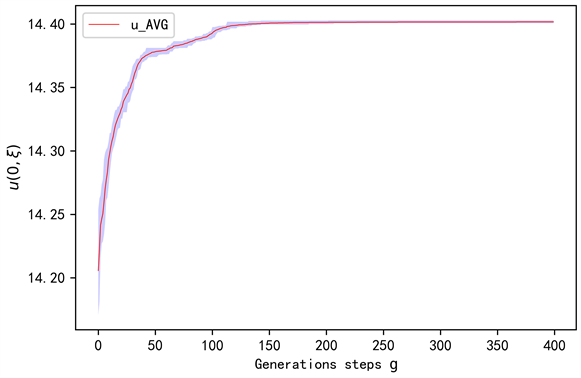
Figure 9. Solution of 12-dimensional Investment and Consumption problem against generations steps g

图9. 12-维投资消费问题的解随进化代数g的变化

Table 4. Numerical simulation of 12-dimensional Investment and Consumption problem

表4. 投资消费问题在12-维形式下的数值模拟

Figure 10. Value of function $f_{n,\pi }\left(x;{\varphi }_{n,\pi }\right)$ against x, where $n\in \left\{0,1,\cdots ,N-1\right\}$

图10. 函数 $f_{n,\pi }\left(x;{\varphi }_{n,\pi }\right)$ 随x的变化，其中 $n\in \left\{0,1,\cdots ,N-1\right\}$

Figure 11. Value of function $f_{n,C}\left(x;{\varphi }_{n,C}\right)$ against x, where $n\in \left\{0,1,\cdots ,N-1\right\}$

图11. 函数 $f_{n,C}\left(x;{\varphi }_{n,C}\right)$ 随x的变化，其中 $n\in \left\{0,1,\cdots ,N-1\right\}$

在表4中，我们令进化算法的进化代数为400代，每一代的种群规模 $NP=30$。在进化过程中，我们计算了每一代的最优 $u\left(0,\xi \right)$ 值，相应规模下 $u\left(0,\xi \right)$ 的均值及标准差。图9为12-维投资消费问题(3.12)的解 $u\left(t=0,\xi =25\right)$ 在20个等距时间步的离散下随进化代数g的变化情况。图中的阴影部分表示每一代种群中 $\max u\left(0,\xi \right)$ 和 $\min u\left(0,\xi \right)$ 之间的差值。红色的线表示 $u\left(0,\xi \right)$ 的均值。在400代44232.06秒的进化后，该数值方法获得的解的标准差为5.77984E−04。图10为函数 $f_{n,\pi }\left(x;{\varphi }_{n,\pi }\right)$，其中 ${\varphi }_{n,\pi }$ 为映射 $x_{t_n}\mapsto \pi \left(t_n,x_{t_n}\right)$ 中的参数，由我们在2.2节、2.3节推导出的算法求解得出，自变量 $x\in \left\{-5,\cdots ,5\right\}\in ℝ$ ；同样的，图11为函数 $f_{n,C}\left(x;{\varphi }_{n,C}\right)$。

在图9关于 $u\left(0,r\left(0\right),{\eta }_0,\xi \right)$ 的计算中，我们将它的真实解由14.4029代替。

4. 结论

本文通过提出一种新型的算法，避开求解值函数，能够普适性的解决带有策略函数的线性、非线性随机控制问题，获得足够精确的数值解。在实际算例的背景下，显示出算法能够求解工程、金融等领域的相关问题，具有一定的实际意义。由于使用深度学习算法和进化算法两种智能算法进行架构，不可避免地造成了整个算法时间相对较长，在迁移应用中需要针对问题做好理论支撑，避免冗余设置造成的计算时间增加。

附录

3.1节中5-维Riccati方程的参数设计

当 $d=5$， $m=5$ 时，我们有 式中 $\sigma \left(t,x_t;v_t\right)\text{d}{W}_t={\displaystyle \underset{i=1}{\overset{5}{\sum }}\left(C^i{x}_t+D^i{v}_t\right)\text{d}{W}_t^i}$。

其中

$C^1=\left(\begin{array}{ccccc}0.1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0.1& 0& 0\\ 0& 0& 0& 0.1& 0\\ 0& 0& 0& 0& 0.02\end{array}\right)$, $C^2=\left(\begin{array}{ccccc}0.02& 0& 0& 0& 0\\ 0& 0.3& 0& 0& 0\\ 0& 0& 0.01& 0& 0\\ 0& 0& 0& 0.1& 0\\ 0& 0& 0& 0& 0\end{array}\right)$, $C^3=\left(\begin{array}{ccccc}0.1& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0.1& 0& 0\\ 0& 0& 0& 0.1& 0\\ 0& 0& 0& 0& 0.03\end{array}\right)$,

$C^4=\left(\begin{array}{ccccc}0.02& 0& 0& 0& 0\\ 0& 0.03& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0.1& 0\\ 0& 0& 0& 0& 0\end{array}\right)$, $C^5=\left(\begin{array}{ccccc}0.02& 0& 0& 0& 0\\ 0& 0.1& 0& 0& 0\\ 0& 0& 0.02& 0& 0\\ 0& 0& 0& 0.11& 0\\ 0& 0& 0& 0& 0.02\end{array}\right)$.

$D^1=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0.01& 0& 0& 0\\ 0& 0& 0.02& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0.01\end{array}\right)$, $D^2=\left(\begin{array}{ccccc}0.03& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0.1& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)$, $D^3=\left(\begin{array}{ccccc}0.01& 0& 0& 0& 0\\ 0& 0.01& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\end{array}\right)$,

$D^4=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 0& 0.02& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0.02& 0\\ 0& 0& 0& 0& 0\end{array}\right)$, $D^5=\left(\begin{array}{ccccc}0.03& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 0.02& 0\\ 0& 0& 0& 0& 0\end{array}\right)$.

NOTES

^*通讯作者。