关于某些连续函数线性组合的分形维数估计

A Remark on the Fractal Dimensions Estimation of the Linear Combination of Continuous Functions

摘要: 本文主要研究了某类分形函数线性组合的分形维数。讨论了具有不同上、下Box维数分形函数线性组合的上、下Box维数估计，得到如下结果。一些情形下，线性组合函数具有与原函数相关的上Box维数或下Box维数。而其他情形下，线性组合函数的上、下Box维数数值均是不确定的。

Abstract: In the present paper, we mainly investigate the fractal dimensions of the linear combination of certain fractal functions. We discuss the estimation of Upper and Lower Box dimension of the linear combination of fractal functions having different Upper and Lower Box dimension, and have obtained the following results. In some cases, the linear combination function has Upper or Lower Box dimension that is related to the original function. In other cases, Upper and Lower Box dimen-sion of the linear combination function is uncertain.

1. 引言

在经典的微积分理论研究中，我们知道单位区间上两个连续函数的任意线性组合一定还是一个连续函数。而很多连续函数具有一定的分形维数。因此我们感兴趣的是，连续函数线性组合的分形维数变化情况。

过去的研究已经发现了许多具有分形维数的连续函数。典型的例子有Weierstrass函数 [1]、自仿射函数 [1]、线性分形插值函数 [2]、Bush函数 [3] 等。此外，参考文献 [4] 和 [5] 中分别给出了具有Box维数为2和1的连续函数的示例。

关于函数图像的分形维数估计的技巧与方法已经建立，Hu讨论了Weierstrass类函数的分形维数和奇点 [6]。梁永顺研究了连续函数分数阶微积分的分形维数估计问题 [5]。Hyde对典型连续函数图像的Box维数进行了研究 [7]，证明了对于一个典型的一致连续函数 $f(x)$ ，其图像的下Box维数可以尽可能小，而图像的上Box维数可以尽可能大。

许多学者们已经注意到分形函数线性组合的分形维数估计。这些研究具有十分重要的意义。 [8] 中，作者对具有不同Box维数分形函数的线性组合进行了初步讨论。 [9] 和 [10] 中，作者进一步研究了具有相同Box维数的分形函数线性组合情形，证明了：1) 所有具有Box维数1的分形函数是一个分形线性空间；2) 所有具有相同Box维数 $s\left(1<s\le 2\right)$ 的分形函数不是一个线性空间。在此研究基础上，可以对上述问题进行进一步讨论，并给出进一步的研究成果。

然而，我们仍然有持续关注的问题。如果 $f\left(x\right)$ 的Box维数存在，而 $g\left(x\right)$ 没有Box维数，我们可以研究 $f\left(x\right)$ 和 $g\left(x\right)$ 的线性组合Box维数是否存在。当 $a\cdot f\left(x\right)+b\cdot g\left(x\right)$ 的Box维数不存在时， $a\cdot f\left(x\right)+b\cdot g\left(x\right)$ 的上Box维数和下Box维数取值如何计算。我们还可以考虑两个Box维数不存在的连续函数线性组合的上、下Box维数。该研究对于丰富分形函数理论以及在其它学科的应用有着重要的实际意义。

在本文中，我们主要研究两个Box维数不存在的连续函数线性组合的分形维数。我们首先给出了上、下Box维数和Box维数的定义与有关引理，然后根据两个连续函数上、下Box维数的关系进行分类讨论，对其中的一些情形给出了理论推导与证明，最后补充的函数图像与数值模拟进一步证明了我们得到的一些结论。

2. 定义及符号

令I为单位区间 $\left[0,1\right]$ ， $C\left(I\right)$ 为I上所有连续函数的集合。不做特别说明时，本文讨论的函数都是I上的连续函数。 $f\left(x\right)$ 的图像记作

$\Gamma \left(f,I\right)=\left\{\left(x,f\left(x\right)\right):x\in I\right\}.$

本文使用的分形维数是上、下Box维数和Box维数。

定义2.1 [1].

令 $f\left(x\right)\in C\left(I\right)$ 为I上的有界子集， $N_{\delta }\Gamma \left(f,I\right)$ 是可以覆盖f集的最少的 $\delta$ 网立方体个数，则函数图像上、下Box维数分别定义为

${\underset{\_}{\dim }}_B\Gamma \left(f,I\right)=\underset{\delta \to 0}{\underset{\_}{\lim }}\frac{\log N_{\delta }\Gamma \left(f,I\right)}{-\log \delta }$ (2.1)

和

${\bar{\dim }}_B\Gamma \left(f,I\right)=\underset{\delta \to 0}{\bar{\lim }}\frac{\log N_{\delta }\Gamma \left(f,I\right)}{-\log \delta }.$ (2.2)

如果这两个值相等，则称这共同的值为f的Box维数，记为

${\dim }_B\Gamma \left(f,I\right)=\underset{\delta \to 0}{\lim }\frac{\log N_{\delta }\Gamma \left(f,I\right)}{-\log \delta }.$ (2.3)

令 $D_s\left(I\right)$ 是所有在I上具有Box维数 $s\left(1\le s\le 2\right)$ 的函数的集合，令 $D_{s_1}^{s_2}\left(I\right)$ 是所有在I上具有上Box维数 $s_2$ ，下Box维数 $s_1\left(1\le s_1\le s_2\le 2\right)$ 的函数的集合。如果 $s_1=s_2$ ，则 $D_{s_1}^{s_2}\left(I\right)=D_{s_1}\left(I\right)$ 。

关于分形维数的进一步讨论和其他定义可以在文献 [1] 和 [11] [12] [13] 中找到。根据定义2.1，可以得出以下基本结论。

引理2.1 [1].

令 $f\left(x\right)\in C\left(I\right)$ ，则有

$1\le {\underset{\_}{\dim }}_B\Gamma \left(f,I\right)\le {\bar{\dim }}_B\Gamma \left(f,I\right)\le 2.$ (2.4)

如果 $\Gamma \left(f,I\right)$ 的Box维数存在，则有

$1\le {\dim }_B\Gamma \left(f,I\right)\le 2.$ (2.5)

由引理2.1可知，任意一个闭区间上的连续函数，总有上Box维数的自然上界2以及下Box维数的自然下界1。

将 $\left[a,b\right]$ 上 $f\left(x\right)$ 最大变化范围写作 $R_f\left[a,b\right]$ ，满足

$R_f\left[a,b\right]=\underset{a\le x,y\le b}{\sup }\left|f\left(x\right)-f\left(y\right)\right|.$

因为我们在本文中主要讨论连续函数，所以给出以下引理。

引理2.2 [1].

令 $f\left(x\right)\in C\left(I\right)$ ， $\delta \in \left(0,1\right)$ ，m是不小于 ${\delta }^{-1}$ 的最小整数。将 $N_{\delta }\Gamma \left(f,I\right)$ 表示为与 $\Gamma \left(f,I\right)$ 相交的 $\delta$ 网立方体个数，则有

${\displaystyle \underset{i=0}{\overset{m-1}{\sum }}\max }\left\{\frac{R_f\left[i\delta ,\left(i+1\right)\delta \right]}{\delta },1\right\}\le N_{\delta }\Gamma \left(f,I\right)\le 2m+{\delta }^{-1}{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_f}\left[i\delta ,\left(i+1\right)\delta \right].$

3. 主要结论

在本节中，我们将给出Box维数不存在的分形函数线性组合的分形维数估计。在有些情形下，可以算出线性组合函数的分形维数，并发现其与原函数存在一定的联系，而在有些情形下可以证明线性组合函数的上(下)Box维数是不确定的。

令 $f\left(x\right)\in D_{s_1}^{s_2}\left(I\right)$ ， $g\left(x\right)\in D_{s_3}^{s_4}\left(I\right)$ 。若 $a=b=0$ ，则有

${\dim }_B\Gamma \left(af+bg,I\right)={\dim }_B\Gamma \left(0,I\right)=1.$

如果 $a\ne 0,b=0$ ，有 $af\left(x\right)+bg\left(x\right)=af\left(x\right)$ ，此时 $af\left(x\right)+bg\left(x\right)\in D_{s_1}^{s_2}\left(I\right)$ 。同样的 $a\ne 0,b=0$ ，则有 $af\left(x\right)+bg\left(x\right)\in D_{s_3}^{s_4}\left(I\right)$ ，现在我们考虑当 $a\cdot b\ne 0$ 时， $f\left(x\right)$ 和 $g\left(x\right)$ 的非平凡线性组合的分形维数。

首先，令 $f\left(x\right)$ 的下Box维数大于 $g\left(x\right)$ 的上Box维数，即 $s_4<s_1$ ，我们可以得到如下结论。

定理3.1.

令 $f\left(x\right)\in D_{s_1}^{s_2}\left(I\right)$ ， $g\left(x\right)\in D_{s_3}^{s_4}\left(I\right)$ 。当 $s_3<s_4<s_1<s_2$ ，可以得到

${\bar{\dim }}_B\Gamma \left(af+bg,I\right)={\bar{\dim }}_B\Gamma \left(f,I\right)$

和

${\underset{\_}{\dim }}_B\Gamma \left(af+bg,I\right)={\underset{\_}{\dim }}_B\Gamma \left(f,I\right).$

证明.令 $\delta \in \left(0,1\right)$ ，m为大于或等于 ${\delta }^{-1}$ 的最小整数。将 $N_{\delta }\Gamma \left(f,I\right)$ 和 $N_{\delta }\Gamma \left(g,I\right)$ 分别记作与 $\Gamma \left(f,I\right)$ 和 $\Gamma \left(g,I\right)$ 相交的 $\delta$ 网立方体个数。将 $N_{\delta }\Gamma \left(af+bg,I\right)$ 记作与 $\Gamma \left(af+bg,I\right)$ 相交的 $\delta$ 网立方体个数。

由定理条件知， ${\bar{\dim }}_B\Gamma \left(f,I\right)=s_2$ ， ${\bar{\dim }}_B\Gamma \left(g,I\right)=s_4$ 。因此对于 $\forall 0<{\epsilon }_1<2-s_2$ ，存在 ${\delta }_1>0$ ，使得

$N_{\delta }\Gamma \left(f,I\right)\le {\left({\delta }^{-1}\right)}^{s_2+{\epsilon }_1},\delta \in \left(-{\delta }_1,{\delta }_1\right).$

等号成立当且仅当 $\delta \to 0$ ， ${\epsilon }_1\to 0$ 。

对于 $\forall 0<{\epsilon }_2<s_1-s_4$ ，存在 ${\delta }_2>0$ ，使得

$N_{\delta }\Gamma \left(g,I\right)\le {\left({\delta }^{-1}\right)}^{s_4+{\epsilon }_2},\delta \in \left(-{\delta }_2,{\delta }_2\right).$

等号成立当且仅当 $\delta \to 0$ ， ${\epsilon }_2\to 0$ 。

根据引理2.2，

$N_{\delta }\Gamma \left(af+bg,I\right)\le 2m+{\delta }^{-1}{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_{af+bg}}\left[i\delta ,\left(i+1\right)\delta \right].$

由

$R_{af+bg}\left[i\delta ,\left(i+1\right)\delta \right]\le a{R}_f\left[i\delta ,\left(i+1\right)\delta \right]+b{R}_g\left[i\delta ,\left(i+1\right)\delta \right],$

可以得到

$\begin{array}{c}{N}_{\delta }\Gamma \left(af+bg,I\right)\le 2m+a{\delta }^{-1}{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_f\left[i\delta ,\left(i+1\right)\delta \right]}+b{\delta }^{-1}{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_g\left[i\delta ,\left(i+1\right)\delta \right]}\\ \le 2m+a{N}_{\delta }\Gamma \left(f,I\right)+b{N}_{\delta }\Gamma \left(g,I\right)\\ \le 2m+a{\left({\delta }^{-1}\right)}^{s_2+{\epsilon }_1}+b{\left({\delta }^{-1}\right)}^{s_4+{\epsilon }_2}.\end{array}$

当 $\delta \in \left(-{\delta }_3,{\delta }_3\right)$ ， ${\delta }_3=\min \left\{{\delta }_1,{\delta }_2\right\}$ ，对任意 ${\epsilon }_1$ 和 ${\epsilon }_2$ ，

$N_{\delta }\Gamma \left(af+bg,I\right)\le \left(1+a\right){\left({\delta }^{-1}\right)}^{s_2},\left(\epsilon \to 0\right).$

因此

$\begin{array}{c}{\bar{\dim }}_B\Gamma \left(af+bg,I\right)=\overline{\underset{\delta \to 0}{\lim }}\frac{\log N_{\delta }\Gamma \left(af+bg,I\right)}{-\log \delta }\\ \le \overline{\underset{\delta \to 0}{\lim }}\frac{\log \left(1+a\right){\left({\delta }^{-1}\right)}^{s_2}}{-\log \delta }\\ =s_2.\end{array}$

另一方面，对于 $\forall 0<{\epsilon }_2<s_4-s_3,\forall {\delta }_2>0$ ，存在 $\delta \in \left(-{\delta }_2,{\delta }_2\right)$ ，使得

$N_{\delta }\Gamma \left(g,I\right)\ge {\left({\delta }^{-1}\right)}^{s_4-{\epsilon }_2}.$

由引理2.2，

$N_{\delta }\Gamma \left(af+bg,I\right)\ge {\delta }^{-1}{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_{af+bg}}\left[i\delta ,\left(i+1\right)\delta \right].$

易知

${\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_{af+bg}\left[i\delta ,\left(i+1\right)\delta \right]}\ge \left|a{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_f\left[i\delta ,\left(i+1\right)\delta \right]}-b{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_g\left[i\delta ,\left(i+1\right)\delta \right]}\right|.$

类似以上讨论可得，对于足够小的 $\delta$ ，

$b{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_g\left[i\delta ,\left(i+1\right)\delta \right]}\le \frac{a}{2}{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{R}_f}\left[i\delta ,\left(i+1\right)\delta \right].$

则有

${\underset{\_}{\dim }}_B\Gamma \left(af+bg,I\right)\ge \underset{\delta \to 0}{\underset{\_}{\lim }}\frac{\log \left(\frac{a}{2}\right){\left({\delta }^{-1}\right)}^{s_2}}{-\log \delta }=s_2.$

因此

${\bar{\dim }}_B\Gamma \left(af+bg,I\right)={\bar{\dim }}_B\Gamma \left(f,I\right)=s_2.$

与上Box维数类似的讨论，可以得到

${\underset{\_}{\dim }}_B\Gamma \left(af+bg,I\right)={\underset{\_}{\dim }}_B\Gamma \left(f,I\right).$

如果 $f\left(x\right)$ 和 $g\left(x\right)$ 在I上具有相同的上、下Box维数，我们可以得出以下结论。

定理3.2.

令 $f\left(x\right)\in D_{s_1}^{s_2}\left(I\right)$ ， $g\left(x\right)\in D_{s_3}^{s_4}\left(I\right)$ ， $s_2=s_4,s_1=s_3>1$ ，那么当 $f\left(x\right)$ 和 $g\left(x\right)$ 的非平凡线性组合的分形维数存在时，它可以是1到 $s_1\left(s_3\right)$ 之间的任意数。

证明. 令 $a,b\in ℝ$ 且 $a\cdot b\ne 0$ ，记

${\bar{\dim }}_B\Gamma \left(f,I\right)=s_2.$

令 $g\left(x\right)=\frac{-a}{b}f\left(x\right)$ ，则有

${\bar{\dim }}_B\Gamma \left(af+bg,I\right)={\bar{\dim }}_B\Gamma \left(0,I\right)=1.$

令 $g\left(x\right)=\frac{a}{b}f\left(x\right)$ ，可以得到

${\bar{\dim }}_B\Gamma \left(af+bg,I\right)={\bar{\dim }}_B\Gamma \left(2a\cdot f,I\right)=s_2.$

令 $g\left(x\right)=\frac{-a}{b}\left[f\left(x\right)+h\left(x\right)\right]$ ， $h\left(x\right)$ 定义在I上且具有上Box维数 $s\in \left(1,s_2\right)$ ，则有

${\bar{\dim }}_B\Gamma \left(af+bg,I\right)={\bar{\dim }}_B\Gamma \left(-a\cdot h,I\right)=s.$

以上讨论对于下Box维数同样适用。这表明如果 $\Gamma \left(af+bg,I\right)$ 的上(下) Box维数存在，则可以是0和 $s_2\left(s_1\right)$ 间的任意数字。

在定理3.2中，我们假设 $\Gamma \left(f,I\right)$ 和 $\Gamma \left(g,I\right)$ 的下Box维数大于1，现在我们考虑 ${\underset{\_}{\dim }}_B\Gamma \left(f,I\right)={\underset{\_}{\dim }}_B\Gamma \left(g,I\right)=1$ 时的情况。由引理2.1，

${\underset{\_}{\dim }}_B\Gamma \left(af+bg,I\right)\ge 1.$

类似定理3.1的证明，可以得到

${\underset{\_}{\dim }}_B\Gamma \left(af+bg,I\right)\le 1.$

因此

$af+bg\in D_1^s\left(I\right).$

考虑 $\Gamma \left(f,I\right)$ 和 $\Gamma \left(g,I\right)$ 具有不同分形维数的情形，我们可以得到下表1。

Table 1. The fractal dimensions of the linear combination of continuous functions

表1. 连续函数线性组合的分形维数

表1中给出的“不确定”表明相应线性组合的上、下Box维数是不确定的。s也表示不确定的上Box维数或下Box维数。

从上面给出的表中可以得到，对于 $\Gamma \left(f,I\right)$ 和 $\Gamma \left(g,I\right)$ 的某些分形维数，其线性组合上、下Box维数与 $\Gamma \left(f,I\right)$ (或 $\Gamma \left(g,I\right)$ )保持一致；一些情形下，相应线性组合只存在上Box维数或下Box维数；当 $\Gamma \left(f,I\right)$ 和 $\Gamma \left(g,I\right)$ 的上Box维数相等时，其线性组合的上、下Box维数均是不确定的值。

4. 图像

在这一部分，我们会给出几个图例，这些例子进一步说明了我们在上一部分得到的结果。

例4.1 [14].

令 $0<\alpha <1$ ， ${\lambda }_j\nearrow +\infty$ ，Besicovitch函数可记为

$B\left(x\right)={\displaystyle \underset{j\ge 1}{\sum }{\lambda }_j^{-\alpha }\sin }\left({\lambda }_{j}x\right),0<\alpha <1.$

当 $\lambda$ 足够大，并且 ${\lambda }_j={\left({\lambda }_j\right)}^{2^j}$ ，可以得到

${\bar{\dim }}_B\Gamma \left(B,I\right)=2-\alpha ;{\underset{\_}{\dim }}_B\Gamma \left(B,I\right)=\frac{2}{1+\alpha }.$

下面我们给出图例。 $f\left(x\right)$ 和 $g\left(x\right)$ 按如上Besicovitch函数定义。令 $\lambda =2,\alpha =0.2$ ，图1表示 $f\left(x\right)$ 。令 $\lambda =2,\alpha =0.5$ ，图2和图3分别表示 $g\left(x\right)$ 和 $f\left(x\right)+g\left(x\right)$ 。

Figure 1. $f(\; x\; )$

图1. $f(\; x\; )$

Figure 2. $g(\; x\; )$

图2. $g(\; x\; )$

Figure 3. $f\left(x\right)+g(\; x\; )$

图3. $f\left(x\right)+g(\; x\; )$

令 $f\left(x\right)$ 的 $\alpha$ 分别为0.1，0.2，0.3，0.4， $g\left(x\right)$ 的 $\alpha$ 分别为0.5，0.6，0.7，0.8。表2给出了 $\Gamma \left(f,I\right)$ ， $\Gamma \left(g,I\right)$ ， $\Gamma \left(f+g,I\right)$ 的上、下Box维数。

图4展示了 $\Gamma \left(f,I\right)$ 与 $\Gamma \left(f+g,I\right)$ 的下Box维数间的关系；图5展示了 $\Gamma \left(f,I\right)$ 与 $\Gamma \left(f+g,I\right)$ 的上Box维数间的关系。

Table 2. Numerical results

表2. 数值结果

Figure 4. Connection among $\alpha ,{\underset{\_}{\dim }}_B\Gamma \left(f,I\right)$ and ${\underset{\_}{\dim }}_B\Gamma \left(f+g,I\right)$

图4. $\alpha ,{\underset{\_}{\dim }}_B\Gamma \left(f,I\right)$ 和 ${\underset{\_}{\dim }}_B\Gamma \left(f+g,I\right)$ 之间的联系

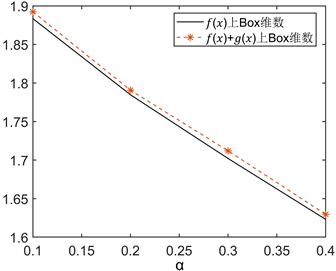
Figure 5. Connection among $\alpha ,{\bar{\dim }}_B\Gamma \left(f,I\right)$ and ${\bar{\dim }}_B\Gamma \left(f+g,I\right)$

图5. $\alpha ,{\bar{\dim }}_B\Gamma \left(f,I\right)$ 和 ${\bar{\dim }}_B\Gamma \left(f+g,I\right)$ 之间的联系

5. 结论

本文主要研究I上具有一定分形维数的两个连续函数线性组合的分形维数估计。这里使用的分形维数主要是Box维数和上、下Box维数。当连续函数具有不同上Box维数时，具有较大上Box维数的函数能够吸收具有较小上Box维数的函数。换言之，连续函数线性组合的上Box维数是较大的上Box维数。当连续函数具有相同的下Box维数1时，线性组合函数的下Box维数也为1。在其他一些情形下，连续函数线性组合的上、下Box维数可能是不确定的值。

除了Box维数，人们还可以研究其它分形维数，如两个连续函数线性组合的Hausdorff维数 [1]、Krull维数 [6]、填充维数 [1] 和维纹 [15] 等。

这里研究的连续函数是在 $ℝ$ 上的闭区间上定义的。它们的分形维数不超过2且不低于1。在此基础上，我们可以继续探索定义在 ${ℝ}^2$ 上的分形曲面的线性组合的分形维数。如果分形曲面的Box维数存在，则必须不超过3且不小于2。然而，相应的分形曲面线性组合的分形维数的估计要困难得多。

基金项目

感谢国家自然科学基金(批准号12071218)、江苏省自然科学基金(批准号BK20161492)和中央高校基础研究经费(批准号30917011340)的支持。

NOTES

^*通讯作者。