1. 引言
在城市经济飞速发展的同时,环境治理问题日益突出,空气质量问题逐渐成为人们共同关注的重要话题 [1]。污染物浓度一年又一年的加剧促使呼吸道疾病的发病率明显呈上升趋势。近年来,由于污染治理不到位,多地遭遇较强的雾霾,雾霾降低了能见度,使得城市交通系统几度陷入瘫痪,同时给人体健康带来了不能忽略的负面影响。可见建立合理的空气质量预报模型,提前获知可能发生的大气污染过程并采取相应控制措施势在必行 [2]。
BP (back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,是目前应用最广泛的神经网络。BP神经网络能学习和贮存大量的输入、输出模式映射关系,而无需事前解释描述这种映射关系的数学方程。它的学习规划则是使用最速下降,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input layer)、隐藏层(hide layer)和输出层(output layer)。
BP神经网络具有以下优点:1) 具有较强的非线性映射能力,这使得其特别适合于求解内部机制复杂的问题;2) 具有高度自学习的自适应能力,具有将学习成果应用于新知识的能力;3) 具有一定的容错能力;4) 简单、易操作、计算量小、并行性。
目前常用的预报空气质量的模型为WRE-CMAQ模拟体系。WRE是集数值天气预报、大气模拟、数据同化于一体的模型系统,主要用于大气环境模拟、天气研究、气象预报等 [3] [4] [5];CMAQ模型主要用于环境规划、环境保护标准、环境影响评价等有关政策的制定与编制。虽然WRE-CMAQ模拟体系起到了不错的效果,但是由于精确性不是很高,故需要进行二次建模 [6]。
2. 符号说明
表1,表2,表3,表4都是进行相关的解释,为之后的建立模型做铺垫。

Table 1. System resulting data of standard experiment
表1. 标准试验系统结果数据

Table 5. Air quality sub-index (IAQI) and the corresponding concentration limits of pollutant item
表5. 空气质量分指数(IAQI)及对应的污染物项目浓度限值
注:1) 臭氧(O3)最大8小时滑动平均浓度值高于800的,不再进行其空气质量分指数计算。2) 其余污染物浓度高于IAQI = 500对应限值时,不再进行其空气质量分指数计算。
表5是空气质量分指数及对应的污染物项目浓度限值,可以看出二氧化硫空气质量分数偏高。
3. 数据分析与处理
使用SPSS统计软件,分别得出各污染物浓度与各气象条件的相关性:

Table 6. Correlation of each pollutant concentration with each measured meteorological condition
表6. 各污染物浓度与各实测气象条件的相关性
**在0.01级别(双尾),相关性显著。*在0.05级别(双尾),相关性显著。
由表6知,实测气象条件中SO2的浓度与湿度呈较强的负相关性,NO2的浓度与风速呈较强的负相关性,PM10的浓度与湿度呈较强的负相关性,PM2.5的浓度与气压呈较强的正相关性,O3的浓度与湿度呈较强的负相关性,CO的浓度与温度呈较强的正相关性。由此得到湿度有利于SO2、PM10、O3的扩散或沉降,风速有利于NO2的扩散或沉降,气压有利于PM2.5的扩散或沉降,而温度有利于CO的扩散或沉降。反之,风速和风向相对湿度不利于SO2的扩散或沉降,同样湿度和风向相对风速不利于NO2的扩散或沉降,温度和风向相对湿度不利于PM10 的扩散或沉降,风向相对于气压不利于PM2.5的扩散或沉降,风向和气压相对湿度不利于O3的扩散或沉降,同样风向和气压相对温度不利于CO的扩散或沉降。(这里指的是采用皮尔逊(Pearson)相关系数得到的变量间的相关性分析,相关系数的绝对值越大,相关性越强:相关系数越接近于1或−1,正或负相关度越强,相关系数越接近于0,相关度越弱。)
使用Python画出各污染物在所给时间范围内的月平均质量浓度与各气象条件的趋势关系图如下:
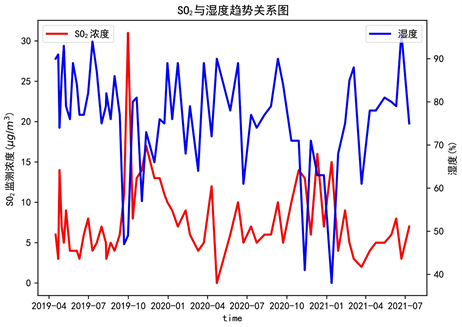
Figure 1. Trend of SO2 vs. humidity
图1. SO2与湿度的趋势关系图
图1为SO2与湿度的趋势关系图,观察得知SO2和湿度整体呈明显的负相关趋势,即随着的湿度的增大,SO2的浓度减小;反之随着湿度的减小,SO2的浓度增大。

Figure 2. Trend of NO2 versus wind speed
图2. NO2与风速的趋势关系图
图2为NO2与风速的趋势关系图,观察得知NO2和风速整体呈明显的负相关趋势,即随着风速的增强,NO2的浓度缩小;反之随着风速的减弱,NO2的浓度增大。

Figure 3. Trend graph of PM10 vs. humidity
图3. PM10与湿度的趋势关系图
图3为PM10与湿度的关系图,观察知PM10和湿度整体呈明显的负相关趋势,即随着湿度的增大,PM10的浓度减小;反之随着湿度的减小,PM10的浓度增大。

Figure 4. Trend of PM2.5 vs. barometric pressure
图4. PM2.5与气压的趋势关系图
图4为PM2.5与气压的趋势关系图,观察知PM2.5和气压整体呈明显的正相关趋势,即随着气压的增大,PM2.5的浓度增大;反之随着气压的减小,PM2.5的浓度减小。
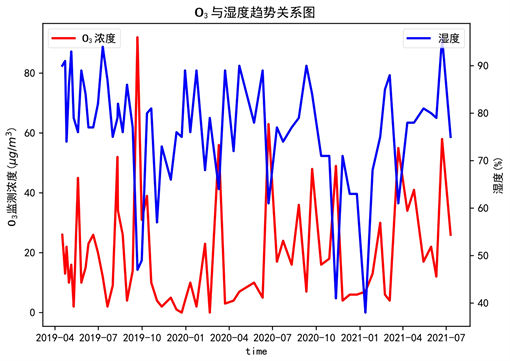
Figure 5. Trend diagram of ozone versus humidity
图5. O3与湿度的趋势关系图
图5为O3与湿度的趋势关系图,观察知O3和湿度整体呈明显的负相关趋势,即随湿度的增大,O3的浓度减小;反之随着湿度的减小,O3的浓度增大。

Figure 6. CO versus temperature trend graph
图6. CO与温度的趋势关系图
图6为CO与温度的趋势关系图,观察知CO和温度整体呈明显的负相关趋势,即随着温度的升高,CO的浓度减小;反之随着温度的降低,CO的浓度增大。
综上所述,对于不同污染物浓度的影响程度,气象条件的分类不同。总的来说比湿、大气压、长波辐射、近地2米温度、湿度有利于O3外各污染物的扩散或沉降;而短波辐射、地面太阳能辐射、潜热通量、感热通量有利于O3的扩散或沉降;相比而言湿度更有利于SO2、PM10、O3的扩散或沉降,风速更有利于NO2的扩散或沉降,气压更有利于PM2.5的扩散或沉降,而温度更有利于CO的扩散或沉降。
4. 二次模型建立
首先,构建数据集。该问题中我们所建立的模型是BP神经网络二次预测模型。该模型的输入数据采用一次预报的气象条件,输出数据则是监测点逐小时污染物浓度与气象一次预报数据污染物浓度与监测点逐小时污染物浓度与气象实测数据污染物浓度的差值,所建模型的功能是构建出输入数据和输出数据的关系,从而找出它们之间存在的规律。BP神经网络模型见图7:

Figure 7. BP neural network model construction process based on forecast base data
图7. 基于预报基础数据的BP神经网络模型构建过程
训练集数据构建步骤如下:
1) 数据时间戳对齐。对于监测点A、B、C的一次预报数据,选择预测时间在上文所述范围的所有数据进行读取,同时读取监测点A、B、C监测时间范围与预测时间范围相同的污染物测量数据。由于在监测点的一次预报数据中,每个运行日期对应三天的逐小时预报数据,且预报数据和实际监测数据各有缺失,因此,我们首先将预报数据中的预测时间和实测数据中的监测时间进行对齐。
2) 生成数据集。在完成时间戳对齐后,我们将选定时间范围内的监测点A、B、C的一次预报气象数据构建为输入数据,每个时间戳的数据看作是一个样本,将每个气象数据对应的污染物一次预报数据和实际监测数据做差,以此作为模型训练集的输出数据。
3) 导入模型。使用python的numpy和pandas库等完成对数据集的构建后,将输入数据和输出数据分别生成两个.mat文件,导入我们的BP神经网络二次预测模型。
接着,构建二次预报模型。综合选题以及网络上的信息我们得知,WRF-CMAQ一次预报模型的结果并不理想,与实测数据的偏差较大,由于实际气象条件对空气质量影响很大(例如湿度降低有利于臭氧的生成),且污染物浓度实测数据的变化情况对空气质量预报具有一定参考价值,因此需要参考空气质量监测点获得的气象与污染物数据进行二次建模,以优化预报模型。
我们将监测点A、B、C一次预报气象数据作为模型输入,将对应的一次预报污染物数据和实测污染物数据的差值作为输出数据,同时利用一次预报的气象数据和实测数据信息,以构建他们之间的关系模型来进行预测。考虑到较大的输入数据量,为了简模型复杂度,我们使用MATLAB构建BP神经网络模型对数据进行建模以获得较好的二次预报数据。
我们将上文中所述构建的数据集导入神经网络模型,模型的相关参数及运行结果如表7:
图8是网络性能函数,在模型训练完成后,我们将监测点A、B、C运行时间在2021年7月13日所获得的2021年7月13日至2021年7月15日的一次预报的气象数据作为输入,获得的模型输出即是要补偿到对应一次预报污染物的数据,将逐小时的一次预报污染物数据相加,得到优化后的逐小时二次预报数据,然后分别将三天的逐小时二次预报数据取平均,得到监测点A、B、C在2021年7月13日至7月15日6种常规污染物的单日浓度值,然后计算相应的AQI和首要污染物。
将所需值代入公式求得监测点A、B、C相应的AQI和首要污染物结果如表8、表9、表10:

Table 8. AQI and primary pollutants measured at monitoring site A since July 13~July 15, 2021
表8. 监测点A自2021年7月13日~7月15日实测的AQI和首要污染物

Table 9. AQI and primary pollutants measured at monitoring site B since July 13~July 15, 2021
表9. 监测点B自2021年7月13日~7月15日实测的AQI和首要污染物

Table 10. AQI and primary pollutants measured at monitoring site C since July 13~July 15, 2021
表10. 监测点C自2021年7月13日~7月15日实测的AQI和首要污染物
由图9和图10的test拟合效果可以看出,经过误差加权后的预测数据其拟合优度系数明显高于初始数据,故误差加权后的预测数据效果要好于初始预测数据,由此说明协同预报模型能够提升针对监测点A、B、C的污染物浓度预报准确度。
5. 结语
本文提出了基于WRE-CMAQ-BP神经网络下的二次建模,先是用SPSS中的皮尔逊相关系数的方法得到各污染物浓度与各气象条件的相关性,然后根据BP神经网络知识进行构建二次预测模型 [7] [8]。本文采用预测监测点A、B、C在2021年7月13日至7月15日六种常规污染物单日浓度的相关数据,发

Figure 9. Initial fitting effect mse
图9. mse初始拟合效果图

Figure 10. Error-weighted fitting effect graph
图10. 误差加权拟合效果图
现二次建模模型比一次预测模型效果更优 [9] [10]。本文的研究成果可以推广到其他未来的研究课题,例如:空气质量的变化预测趋势。