形式三角矩阵环上的强Gorenstein FP-内射模
Strongly Gorenstein FP-Injective Modules over Formal Triangular Matrix Rings
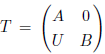
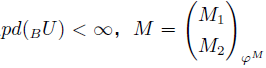
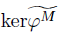
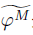
摘要: 本文研究了形式三角矩阵环上的强Gorenstein FP-内射模。 设是形式三角矩阵环，其中 A 和 B 是环， U 是左 B-右 A-双模。证明了若T 是左凝聚环，BU 是有限表示的且是强Gorenstein FP-内射左 T -模，则是强Gorenstein FP-内射左A-模，M2是强Gorenstein FP-内射左B-模，且是满同态。
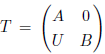
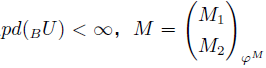
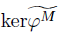
Abstract: This paper considers strongly Gorenstein FP-injective modules over formal triangular matrix rings. Let be formal triangular matrix ring, where A and B are two rings and U is a (B;A)-bimodule. 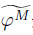It is proved that if T is a left coherent ring, BU is finitely presented and is strongly Gorenstein FP-injective left T-modules, then is strongly Gorenstein FP-injective left A-modules, M2 is strongly Gorenstein FP-injective left B-modules, and is an epimorphism.
文章引用：谭进. 形式三角矩阵环上的强Gorenstein FP-内射模[J]. 理论数学, 2022, 12(7): 1160-1168. https://doi.org/10.12677/PM.2022.127127

参考文献

[1] Enochs, E.E. and Jenda, O.M.G. (1995) Gorenstein Injective and Projective Modules. Mathematische Zeitschrift, 220, 611-633.
https://doi.org/10.1007/BF02572634
[2] Mao, L.X. and Ding, N.Q. (2008) Gorenstein FP-Injective and Gorenstein Flat Modules. Journal of Algebra and Its Application, 7, 491-506.
https://doi.org/10.1142/S0219498808002953
[3] Gao, Z.H. (2013) On Strongly Gorenstein FP-Injective Modules. Communications in Algebra, 41, 3035-3044.
https://doi.org/10.1080/00927872.2012.672601
[4] Mao, L.X. (2020) Duality Pairs and FP-Injective Modules over Formal Triangular Matrix Rings. Communications in Algebra, 48, 5296-5310.
https://doi.org/10.1080/00927872.2020.1786837
[5] 杨银银, 张翠萍. 形式三角矩阵环上的Gorenstein FP-内射模[J]. 山东大学学报(理学版), 2022, 57(2): 38-44.
[6] Haghany, A. and Varadarajan, K. (2000) Study of Modules over Formal Triangular Matrix Rings. Journal of Pure and Applied Algebra, 147, 41-58.
https://doi.org/10.1016/S0022-4049(98)00129-7
[7] Enochs, E.E., Izurdiaga, M.C. and Torrecillas, B. (2014) Gorenstein Conditions over Triangular Matrix Rings. Journal of Pure and Applied Algebra, 218, 1544-1554.
https://doi.org/10.1016/j.jpaa.2013.12.006
[8] 夏国利, 王芳贵. 形式三角矩阵环上的PC-内射模[J]. 四川师范大学学报(自然科学版), 2018, 41(1): 39-43.
[9] Haghany, A., Mazrooei, M. and Vedadi, M.R. (2012) Pure Projectivity and Pure Injectivity over Formal Triangular Matrix Rings. Journal of Algebra and Its Applications, 11, 1-13.
https://doi.org/10.1142/S0219498812501071

为你推荐