沥青路面分析中的非线性问题应用

Application of Nonlinear Problems in Asphalt Pavement Analysis

摘要: 沥青路面是我国公路尤其是高等级公路的主要形式。在沥青路面相关的力学分析中存在大量的非线性问题。本文对沥青路面分析中涉及到的材料非线性问题(包含沥青混合料的粘弹性与粘塑性本构模型)、几何非线性问题(大变形问题)进行探讨，并结合有限元软件对相关非线性问题对相关知识进行应用。研究结果表明：在沥青混合料的力学分析中，考虑材料的非线性能够更准确的描述材料的力学性质，而三轴应力条件下，尤其是较严重的车辙发生时，路表附近的应力计算需要考虑几何非线性。

Abstract: Asphalt pavement is the main form of highway in China, especially high-grade highway. There are a large number of nonlinear problems in the mechanical analysis related to asphalt pavements. Combined with the course, this paper discusses the material nonlinear problems (in-cluding viscoelastic and viscoplasticinstantonal models of asphalt mixtures), geometric nonlinear problems (large deformation problems) involved in the analysis of asphalt pavements, and the ap-plication of related knowledge to the relevant nonlinear problems with finite element software. The results show that considering material nonlinearity in the mechanical analysis of asphalt mixtures can more accurately describe the mechanical properties of the material, while the calculation of stresses near the road surface under triaxial stress conditions, especially when more severe rutting occurs, requires consideration of geometric nonlinearity.

1. 引言

沥青路面是我国公路尤其是高速公路的主要结构形式。截止2017年，90%以上的在运营与在建的高速公里为沥青路面。相较于传统的水泥混凝土路面，沥青路面具有平整度高、铺筑养护便捷、低噪声等一系列优势。与水泥混凝土表现出的高线性、高刚度的性质相比，作为石油化工的重油成分，沥青的化学成分与物理性质复杂。尤其是与石料、改性剂等成分形成沥青混合料后，其性质远非线弹性理论可以解决。

首先，沥青混合料是典型的时间–温度–频率依赖性材料。材料的温度、荷载的作用时间、作用频率都会对材料的力学响应产生显著的影响 [1]。高温低频荷载作用下，材料的性质与无粘结碎石相近，而低温高频荷载作用下，材料的性质与水泥混凝土相近。与房屋建筑相比，公路的工作环境往往更加恶劣，材料的温度受到环境影响剧烈，且公路的荷载具有瞬时性，恒载仅是公路荷载中很小一部分。因此，沥青混合料的粘弹性在沥青路面的分析过程中是一个必须考虑的问题。

其次，高温状态下，沥青路面会发生明显的塑性问题，即车辙。车辙已经成为我国高速公路最严重的病害之一，70%以上的高速公路路面大修与重修与车辙病害相关 [2] [3]。而车辙形成的原因，塑性是典型的材料非线性问题。现阶段工程上应用的主要使用的是线弹性的受力分析结合经验公式，与预测沥青路面的车辙病害。但塑性作为车辙病害的力学成因，在沥青路面的分析中是必须考虑的因素。

此外，沥青路面的车辙往往涉及到的变形往往达到10 mm以上，必然伴随几何非线性问题。该问题在前人的研究往往会被忽视。本文也将对几何非线性问题进行初步的应用，并分析几何非线性问题在研究中的意义。

本文使用有限元软件ABAQUS，从而节省模型创建、离散化、以及刚度组装与求解过程。使用软件的用户材料子程序UMAT进行编写，从而研究材料非线性问题与几何非线性问题。

2. 材料非线性问题

大量的试验与研究表明沥青混合料是一种温度相关，频率相关，荷载相关的材料。沥青混合料是由集料，沥青，石料三相组成混合物，其性质与三种组成均有关系。在高温与低频荷载的作用下，沥青混合料的模量接近于无粘结颗粒材料，在低温与高频荷载的作用下，沥青混合料的模量往往接近甚至高于水泥混凝土的模量。此外，沥青混合料在高应变(应力)荷载的作用下还表现出明显的非线性与不可恢复的塑性特征。因此，沥青混合料是一种典型的热–粘弹–粘塑性材料 [4] [5]。

沥青混合料在荷载作用下的应变，可写为有可恢复的粘弹性应变的形式与不可恢复的粘塑性应变的形式，下式(1)所示：

${\epsilon }_{ij}={\epsilon }_{ij}^{ve}+{\epsilon }_{ij}^{vp}$ (1)

式中： ${\epsilon }_{ij}$ 为沥青混合料在荷载作用下的总应变； ${\epsilon }_{ij}^{ve}$ 为沥青混合料在荷载作用下的粘弹性应变； ${\epsilon }_{ij}^{vp}$ 为沥青混合料在荷载作用下的粘塑性应变。

2.1. 粘弹性本构模型

对于线弹性材料，材料在荷载作用下的应力与应变关系如下式(2)所示：

${\sigma }_{ij}=\frac{1}{3}{\sigma }_{kk}{\delta }_{ij}+S_{ij}=\frac{1}{3}\cdot 3K\cdot {\epsilon }_{kk}{\delta }_{ij}+2G\cdot e_{ij}$ (2)

式中： ${\sigma }_{ij}$， ${\sigma }_{kk}$， $S_{ij}$ 分别为应力张量，体积应力张量，偏应力张量； ${\epsilon }_{kk}$， $e_{ij}$ 分别为体应变张量，偏应变张量；K，G为材料的体积模量与剪切模量； ${\delta }_{ij}$ 为克罗内克符号(Kronecker delta)。

但对于沥青混合料而言，材料的应力–应变具有明显的时间–温度依赖性 [6]。若将时间–温度的影响通过时温等效原理进行统一，则材料的粘弹性本构可以写为如下式(3)所示的积分型本构关系。

${\sigma }_{ij}\left(t\right)={\delta }_{ij}{\displaystyle {\int }_0^{t}K\left(\zeta \left(t\right)-\zeta \left(\tau \right)\right)\frac{\partial {\epsilon }_{kk}}{\partial \tau }\text{d}\tau }+{\displaystyle {\int }_0^{t}2G\left(\zeta \left(t\right)-\zeta \left(\tau \right)\right)\frac{\partial e_{ij}^{ve}}{\partial \tau }\text{d}\tau }$ (3)

式中： $\zeta \left(t\right)$ 为材料的环境影响函数，对于沥青混合料而言， $\zeta \left(t\right)$ 主要与温度有关。根据前人研究 [7]， $\zeta \left(t\right)$ 可用下式(4)所示：

$\zeta \left(t\right)=\frac{t}{a_T^{ve}\left(T\right)}$ (4)

式中： $a_T^{ve}$ 为材料的温度偏移因子，有众多的温度偏移因子模型被提出，其中应用较为广泛的是WLF方程，如下式(5)所示：

$\log a_T^{ve}\left(T\right)=-\frac{C_1\left(T-T_{ref}\right)}{C_2+T-T_{ref}}$ (5)

式中：T， $T_{ref}$ 为材料温度与主曲线基准温度，℃； $C_1$ 与 $C_2$ 为材料常数，由实验数据拟合回归得出。

沥青混合料的体积模量与剪切模量严格上属于两个独立的变量，但若将材料的泊松比设为固定值，可由杨氏模量与泊松比将材料的一维形式推导至三维形式见式(6)：

$G\left(t\right)=\frac{E\left(t\right)}{2\left(1+\nu \right)},K\left(t\right)=\frac{E\left(t\right)}{3\left(1-2\nu \right)}$ (6)

式中：E(t)为材料的杨氏松弛模量， $\nu$ 为材料的泊松比。

因此，对于一维积分性粘弹性本构模型，在数值实现的过程中可将荷载作用的时间进行等距离散 [8]，从而获得以下形式见式(7)：

$\begin{array}{c}\sigma \left(t_n\right)={\displaystyle {\int }_0^{t_n}E\left(\zeta \left(t_n\right)-\zeta \left(\tau \right)\right)\frac{\partial \epsilon }{\partial \tau }\text{d}\tau }\\ ={\displaystyle {\int }_0^{t_{n-1}}E\left(\zeta \left(t_n\right)-\zeta \left(\tau \right)\right)\frac{\partial \epsilon }{\partial \tau }\text{d}\tau }+{\displaystyle {\int }_{t_{n-1}}^{t_n}E\left(\zeta \left(t_n\right)-\zeta \left(\tau \right)\right)\frac{\partial \epsilon }{\partial \tau }\text{d}\tau }\end{array}$ (7)

直接利用上式进行计算，需要进行遗传积分的计算，对于存储与计算的消耗均较大，且无法进行长时间的计算。因此，为方便遗传积分的计算，可将松弛模量写为下式Prony级数的形式见式(8)：

$E\left(t\right)=E_{\infty }+{\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_i{\text{e}}^{-\frac{t}{{\rho }_i}}}$ (8)

式中： $E_{\infty }$ 为材料的永久弹性模量，反映粘弹性响应中的线弹性的部分； $E_i$ 与 ${\rho }_i$ 为不同松弛谱下的松弛模量与松弛速率，反映材料中不同组分的松弛特性。

Prony级数是一种离散谱模型 [9]，根据永久弹性模量与松弛谱阶数的不同，可以表示包括Burgers，广义Maxwell模型在内的众多微分型本构的形式。而Prony级数离散谱的本质方便对其进行Laplace变换转换为频域空间，进而与材料的复数模量进行对应。

在积分型本构模型引入Prony级数后，可将本构模型进一步推导成迭代格式见式(9)，从而避免遗积分的计算问题。

$\begin{array}{l}{\displaystyle {\int }_0^{t_{n-1}}E\left(\zeta \left(t_n\right)-\zeta \left(\tau \right)\right)\frac{\partial \epsilon }{\partial \tau }\text{d}\tau }\\ =E_{\infty }\cdot \epsilon +{\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_i{\displaystyle {\int }_0^{t_{n-1}}{\text{e}}^{-\frac{\zeta \left(t_{n-1}\right)+\zeta \left(\Delta t\right)-\zeta \left(\tau \right)}{{\rho }_i}}\frac{\partial \epsilon }{\partial \tau }\text{d}\tau }}\\ =E_{\infty }\cdot \epsilon +{\text{e}}^{-\frac{\zeta \left(\Delta t\right)}{{\rho }_i}}\cdot {\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_i{\displaystyle {\int }_0^{t_{n-1}}{\text{e}}^{-\frac{\zeta \left(t_{n-1}\right)-\zeta \left(\tau \right)}{{\rho }_i}}\frac{\partial \epsilon }{\partial \tau }\text{d}\tau }}\\ =E_{\infty }\cdot \epsilon +{\text{e}}^{-\frac{\zeta \left(\Delta t\right)}{{\rho }_i}}\cdot \sigma \left(t_{n-1}\right)\end{array}$ (9)

2.2. 粘塑性本构模型

对于沥青混合料永久变形行为的描述，许多研究人员认为其是一种不可恢复的粘弹性或非线性粘弹性，但粘弹性理论无法解释材料在荷载作用下永久变形的方向性问题 [10]。对于沥青混合料而言，尤其是密集配沥青混合料，在高温状态下，由于沥青材料的受热膨胀，混合料几乎处于一种不可压缩的状态，粘弹性产生压缩变形在永久变形中所占的比重很有限。而无论是实际路面的观测还是室内试验的研究观测，均发现沥青混合料的永久变形并非是由材料压缩产生，而主要与材料在偏应力作用下材料的横向滑移有关。而粘塑性理论能够在材料的粘弹性力学响应的基础上，描述材料在偏应力作用下的具有方向特征的永久变形的性质。其基本形式如下式(10)所示：

${\stackrel{\dot{}}{\epsilon }}_{ij}^{vp}={\Gamma }^{vp}{\langle f\rangle }^N\frac{\partial g}{\partial {\sigma }_{ij}}$ (10)

式中： ${\stackrel{\dot{}}{\epsilon }}_{ij}^{vp}$ 为材料的粘塑性应变率；g为材料的势函数，表征材料的粘塑性应变在各个方向上的趋势； ${\Gamma }^{vp}$，N为材料的粘塑性参数，由实验数据回归拟合得出。

上述所示的粘塑性本构模型的基本形式已被广泛的认可，但在屈服函数的具体形式方面还是有很大差异，屈服函数f可以统一写为下式(11)所示形式：

$f=A\cdot \sqrt{J_2}-B\cdot I_1-c$ (11)

式中： $J_2$ 为偏应力第二不变量，c为材料的粘聚力。系数A，B在不同的模型中具有不同的表现形式，如表1所示。

Table 1. Different expressions of coefficients A and B

表1. 系数A，B的不同表现形式

表中：

$\theta =\frac{1}{3}\arccos \left[\frac{3\sqrt{3}}{2}\frac{J_3}{{\left(J_2\right)}^{3/2}}\right]$

$\mu =\frac{2\sqrt{1-d+d^2}}{\sqrt{3}d},\gamma =-\frac{3\sqrt{3}}{2}\frac{\left(1-d\right)d}{{\left(1-d+d^2\right)}^{1.5}},d=\frac{3-\sin \Phi }{3+\sin \Phi }$ (12)

而对于粘聚力模型，沥青混合料相关的研究则较为统一，为下式(13)所示的硬化模型：

$c=a_T^c\left[c_0+c_1\left(1-{\text{e}}^{-c_2{\epsilon }_e^{vp}}\right)\right]$ (13)

式中： $c_0$， $c_1$， $c_2$ 为材料参数； $a_T^c$ 为粘聚力温度偏移因子； ${\epsilon }_e^{vp}$ 为粘塑性有效应变，如下式(14)所示：

${\epsilon }_e^{vp}=\sqrt{\frac{2}{3}{\epsilon }_{ij}^{vp}{\epsilon }_{ji}^{vp}}$ (14)

本文以粘弹性本构模型与D-P粘塑性本构模型为例 [11] [12]，在有限元建立沥青混合料试验中常见的圆柱形试件，模拟沥青混合料的动态模量试验与重复荷载蠕变试验，从而对本文上述的粘弹性本构模型与粘塑性本构进行推导与应用 [13]。有限元建模如图1所示。

Figure 1. Cylindrical finite element model

图1. 圆柱形有限元模型

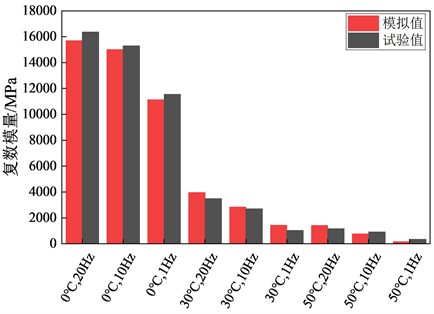
Figure 2. Comparison of experimental and simulated values of complex modulus

图2. 复数模量的试验值与模拟值对比

如图2，在路面的正常工作温度范围内，根据本文的热粘弹性本构模型以及数值计算方法所建立的有限元模型，所得出的沥青混合料的复数模量模拟值与试验值之间具有非常高的一致性。其中相对误差最大值发生在50℃，1 Hz，相对误差为50.8%，但此时绝对误差仅171 MPa，其主要原因在于热粘弹性本构模型中温度调整函数的拟合在高温段存在误差，以及材料的动态模量试验在高温时本身所具有的离散型。因此，模型除在高温低频荷载条件下的模量与试验值相对误差较大外，其余条件下的均能够很好的描述材料的应力应变响应。高温低频条件下尽管模量的相对误差较大，但该条件在实际路面状况下仅在高温条件下车辆低速行驶方可遇到，此外，由于此时材料的模量较小，对结构的整体受力影响较小。

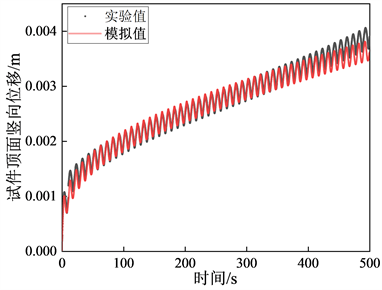
Figure 3. Repeated creep test value compared with simulated value

图3. 重复蠕变试验试验值与模拟值对比

重复蠕变试验试验值与模拟值对比见图3，如图3所示：模拟值与实验值的对比显示，该粘塑性本构模型与数值方法在蠕变的第一与第二阶段均具有较好的适用性。由于本构中不含有第三阶段的描述，因此进入蠕变的第三阶段后模拟值与试验值开始分离。因此，由于材料的塑性的第三阶段开始材料进入破坏阶段，设计到材料的损伤与破坏，粘塑性本构模型无法单独描述。但本文所述的D-P粘塑性本构模型已能够较好的描述塑性模型的第一阶段与第二阶段。

3. 几何非线性问题

小变形是固体力学中的一项重要的假设，小变形假设物体在荷载的作用下变形远小于物体本身，使得变形后的物体与变形前相比几乎相同 [14]。这就简化了变形前后应力与应变计算时的面积与长度的不统一。大变形条件下，材料的荷载作用下构型会发生明显的变化，尤其是刚体转动并不产生变形，但在小变形的理论种会将刚体转动造成的影响计算在内，产生计算的误差。

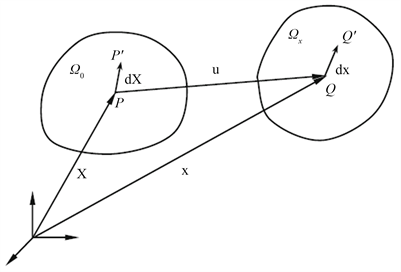
Figure 4. Configuration ${\Omega }_0$ and ${\Omega }_x$ before and after deformation

图4. 变形前后构型 ${\Omega }_0$ 与 ${\Omega }_x$

如图4所示，连续体在荷载作用下由变形前的参考构型，变为变形后构型。构型中一向量PP'变形为向量QQ'。P与Q分别由向量X与x表示。而向量 $x=\left[x1,x2,x3\right]$ 可以表示为向量X的函数，见式(15)：

$\begin{array}{l}x1=x1\left(X1,X2,X3\right)\\ x2=x2\left(X1,X2,X3\right)\\ x3=x3\left(X1,X2,X3\right)\end{array}$ (15)

或表示为参考构型与变形的和的形式，如下式(16)所示：

$x=\Phi \left(X,t\right)=X+u\left(X,t\right)$ (16)

而对于P点的临域，临域处的单位变形可表示为式(17)：

$dx=\frac{\partial x}{\partial X}dX$ (17)

而单位变形 $\frac{\partial x}{\partial X}$ 即为连续体的变形梯度，可以表示为位移的梯度的形式见式(18)：

$F_{ij}=\frac{\partial x}{\partial X}=\frac{\partial \left(X+u\right)}{\partial X}=1+\frac{\partial u}{\partial X}=1+\nabla u$ (18)

对于几何非线性问题，其荷载在于考虑大变形后连续体的应力与应变计算问题 [15]。对于应变问题，需要考虑连续体的单位长度在变形前后的差异；对于应力问题，需要考虑应力方向，以及变形后单位面积的大小。

材料变形前后的差异可由下式计算得出式(19)：

$\begin{array}{c}{\left|dx\right|}^2-{\left|dX\right|}^2=d{x}^{\text{T}}dx-d{X}^{\text{T}}dX\\ =d{X}^{\text{T}}{F}^{\text{T}}FdX-d{X}^{\text{T}}dX\\ =d{X}^{\text{T}}\left(F^{\text{T}}F-1\right)dX\end{array}$ (19)

其中 $\left(F^{\text{T}}F-1\right)$ 即为变形前后的单位长度差异相较于变形前参考构型的单位长度。因此，相较于参考构型，

材料的应变可以表示为式(20)：

$E=\frac{1}{2}\left(F^{\text{T}}F-1\right)=\frac{1}{2}\left(\frac{\partial u}{\partial X}+\frac{\partial u^{\text{T}}}{\partial X}+\frac{\partial u^{\text{T}}}{\partial X}\frac{\partial u}{\partial X}\right)=\frac{1}{2}\left(\nabla u+\nabla u^{\text{T}}+\nabla u^{\text{T}}\nabla u\right)$ (20)

式中：E成为拉格朗日应变。

事实上，上式也可以直接反应出大变形问题与小变形问题的核心差异。其中式中的前两项为小变形问题中的柯西应变，即式(21)：

$\epsilon =\frac{1}{2}\left(\frac{\partial u}{\partial X}+\frac{\partial u^{\text{T}}}{\partial X}\right)$ (21)

小变形假设下，第三项涉及的刚体转动为二阶小量，可以忽略不计，但大变形问题下，刚体转动项的忽略使得本不会影响到应力计算的刚体转动对应变的计算产生影响。因此，大变形问题下，拉格朗日应力更适合进行计算。

对于应力的计算，需要考虑变形对单位面积以及面积法线的影响，变形前后法线与面积可由下式(22)关系表示：

$nd{S}_x=J{F}^{-T}Nd{S}_0$ (22)

式中：n，N分别为变形后与变形前的法线向量； $d{S}_x$， $d{S}_0$ 分别为变形后与变形前的单位面积；J为雅克比行列式值，即 $J=\det \left(F\right)$。

因此，对于单位面积上的荷载而言，可以表示为变形后与变形前的两种形式，即式(23)：

$df=d{S}_{x}n\sigma =d{S}_{0}N{P}^{\text{T}}$ (23)

式中：P被称为第一基尔霍夫应力张量，表示参考构型的应力，即式(24)：

$P=J{F}^{-1}\sigma$ (24)

而第一基尔霍夫应力仍然与变形梯度相关，在第一基尔霍夫应力的基础上，消除变形梯度的影响，可获得第二基尔霍夫应力张量，见式(25)：

$S=P{F}^{-\text{T}}=J{F}^{-1}\sigma F^{-\text{T}}$ (25)

从上述的推导可以看出，大变形问题与小变形问题的核心在于应力应变的计算。而朗格朗日应变与基尔霍夫应力是依据参考构型，即未变形的连续体进行计算的，不受连续体的变形影响。因此，几何非线性问题可以进一步转换为材料非线性问题，从柯西应力应变转变为朗格朗日应变与基尔霍夫应力为函数的本构模型问题。

首先考虑单轴应力条件下的几何非线性问题 [16]。如图5所示，建立四棱柱的有限元模型，并控制模型的轴向应变在−0.2~0.2之间。图中透明部分为原构型，实体部分为压缩应变0.2条件下的构型。

Figure 5. Axial stress model

图5. 轴向应力模型

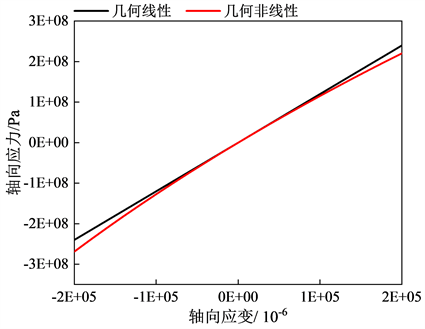
Figure 6. Comparison of geometric linear and geometric nonlinear solutions under axial loading

图6. 轴向荷载下几何线性与几何非线性解比较

如图6所示，为轴向荷载作用下，四棱柱的轴向应力几何非线性与几何线性解的对比。由图中可知，在轴向应变小于0.1时，即总变形小于原物体的10%以下时，轴向应力的差异并不显著。事实上，由于几何非线性问题与小变形问题的解的差异主要集中在刚体旋转上，单轴应力状态下的几何非线性主要是由于材料拉伸与压缩产生的横截面积变化而变化，受到材料泊松比的直接影响。

由于0.2的应变已经远超大部分材料的变形极限，因此土木工程材料，无论是沥青混合料还是水泥混凝土在单轴应力状态下，都可以忽略几何非线性的影响。

图7所示为沥青混合料疲劳试验常进行的四点弯曲小梁试验的有限元模型。控制跨中挠度为0~50 mm。图中透明部分为原构型，实体部分为跨中挠度为50 mm条件下的构型。

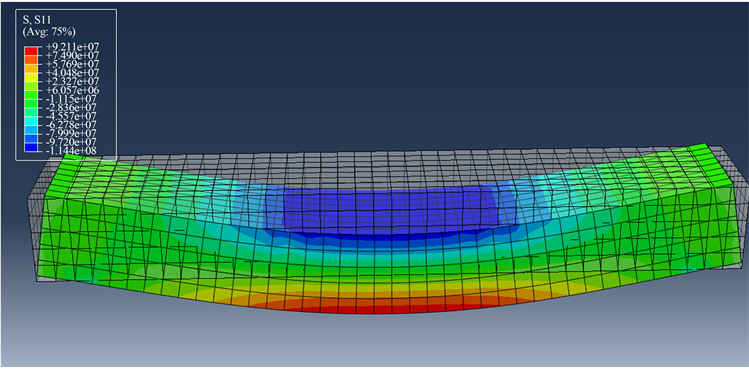
Figure 7. Four-point bending trabecular model

图7. 四点弯曲小梁模型

四点弯曲小梁试验，试验规程中推荐的计算方式为材料力学解。图8所示的为材料力学计算方法以及两种有限元计算方法的比较。图中可以看出在大变形条件下，考虑了几何非线性的影响下，跨中应力与跨中挠度近似呈线性关系，但不考虑几何非线性的材料力学解与有限元解均与几何非线性解有较大的差异。由图中可知，弯曲荷载作用下，几何非线性的影响远大于轴向应力条件，当跨中挠度大于20 mm时，三者的差异已经达到了一倍以上。

而在沥青路面的计算中，随着车辙的发展，路面表面的车辙深度往往达到20 mm以上，路表附近的应力如按照未变形的初建路面进行计算的话将于实际状况有相当大的误差 [17]。因此在三轴应力条件下，尤其是材料发生大的弯曲(即产生可观的刚体转动时)，应当考虑几何非线性对于计算的影响。

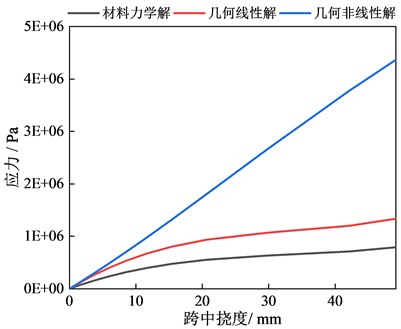
Figure 8. Comparison of geometrically linear and geometrically nonlinear solutions under bending loads

图8. 弯曲荷载下几何线性与几何非线性解比较

4. 总结

本文对沥青路面分析中常见的两种材料非线性问题(粘弹性本构模型与粘塑性本构模型)进行了应用，对几何非线性问题进行了初步的应用。在沥青混合料的力学分析中，考虑材料的非线性能够更准确的描述材料的力学性质，而三轴应力条件下，尤其是较严重的车辙发生时，路表附近的应力计算需要考虑几何非线性。