拟微分算子在Besov空间上的有界性
On the Boundedness of Pseudo-Differential Operators on Besov Spaces
DOI: 10.12677/AAM.2023.123086, PDF, HTML,  被引量   
作者: 蔡士瑛：浙江师范大学数学系, 浙江 金华
关键词: 拟微分算子；HÖrmander类；Besov空间；Pseudo-Differential Operator； HÖrmander Class； Besov Space
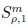
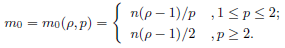
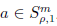
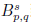
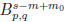
摘要: 在本文我们考虑振幅a属于HÖrmander类时的拟微分算子Ta在Besov空间上的有界性. 对于0 ≤ ρ ≤ 1, p ≥ 1, 令如果且s > m − m0, 我们证明拟微分算子Ta是Besov空间到的有界算子. 这个结果推广了Stein的一个小结果.
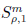
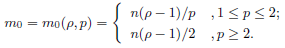
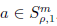
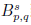
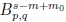
Abstract: In this note, we consider the boundedness of the pseudo-differential operator Ta whose symbol a belongs to HÖrmander class on Besov spaces.Let 0 ≤ ρ ≤ 1, p ≥ 1 If and s > m − m0, then the pseudo-differential operator Ta is bounded from to . And our work is to generalize a result of Stein.
文章引用：蔡士瑛. 拟微分算子在Besov空间上的有界性[J]. 应用数学进展, 2023, 12(3): 837-846. https://doi.org/10.12677/AAM.2023.123086

参考文献

[1] H¨ormander, L. (1965) Pseudo-Differential Operators. Communications on Pure and Applied Mathematics, 18, 501-517.
https://doi.org/10.1002/cpa.3160180307
[2] Kohn, J.J. and Nirenberg, L. (1965) An Algebra of Pseudo-Differential Operators. Communica- tions on Pure and Applied Mathematics, 18, 269-305.
https://doi.org/10.1002/cpa.3160180121
[3] H¨ormander, L. (1967) Pseudo-Differential Operators and Hypoelliptic Equations. In: Caldero´n, A.P., Ed., Singular Integrals. Proceedings of Symposia in Pure Mathematics, Vol. 10, AMS, Providence, RI, 138-183.
[4] H¨ormander, L. (1971) On the L2 Continuity of Pseudo-Differential Operators. Communications on Pure and Applied Mathematics, 24, 529-535.
https://doi.org/10.1002/cpa.3160240406
[5] Hounie, J. (1986) On the L2-Continuity of Pseudo-Differential Operators. Communications in Partial Differential Equations, 11, 765-778.
https://doi.org/10.1080/03605308608820444
[6] Rodino, L. (1976) On the Boundedness of Pseudo Differential Operators in the Class Lm . Proceedings of the AMS, 58, 211-215.
https://doi.org/10.2307/2041387
[7] Ching, C.H. (1972) Pseudo-Differential Operators with Nonregular Symbols. Journal of Dif- ferential Equations, 11, 436-447.
https://doi.org/10.1016/0022-0396(72)90057-5
[8] Stein, E.M. (1993) Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals (PMS-43). Princeton University Press, Princeton, NJ.
[9] A´ lvarez, J. and Hounie, J. (1990) Estimates for the Kernel and Continuity Properties of Pseudo-Differential Operators. Arkiv Matematik, 28, 1-22.
https://doi.org/10.1007/BF02387364
[10] Guo, J. and Zhu, X. (2022) Some Notes on Endpoint Estimates for Pseudo-Differential Oper- ators.
https://arxiv.org/abs/2201.10724
[11] Kenig, C.E. and Staubach, W. (2007) Ψ-Pseudodifferential Operators and Estimates for Max- imal Oscillatory Integrals. Studia Mathematica, 183, 249-258.
https://doi.org/10.4064/sm183-3-3

为你推荐