1. 引言
假定
中的域,定义D上平方可积解析函数空间
这里
,
表示D上解析函数全体,
表示Lebesgue测度。如果
,记空间
的标准正交基为
,称
为域D的Bergman核,Bergman核在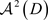 中具有再生性,即对任意
,有
中具有再生性,即对任意
,有
对于包含原点的Reinhardt域D,D上解析函数有以下幂级数表示:
这里
,
,
。并且
是
的标准正交基,因此 [1]
Bergman核在多复变函数论和复几何中起着重要的作用,虽然
中的有界域都存在Bergman核,但其表达式一般没有显示公式,用显式公式计算Bergman核函数是多复变函数论的一个重要研究方向,用Bergman核的显示表达式,可以研究域的陆启铿问题,所谓陆启铿问题指的是一个域是否是陆启铿域,陆启铿域是对所有的
,Bergman核
都不等于零的域,如果一个域是陆启铿域,则它的表示域存在 [2] 。关于Bergman核的计算,可参考综述文献 [3] [4] ,有界域的陆启铿问题研究可参考综述文献 [5] ,近期这方面的研究可参考 [6] [7] [8] [9] 等。在 [7] 和 [9] 中研究了一类无界域——Fock-Bargmann-Hartogs域
的陆启铿问题,本文我们研究另一类无界域(定义见(2.1))的Bergman核的计算,并研究其陆启铿问题。
2. 主要结果
定理2.1. 令
,
(2.1)
则域D的Bergman核为
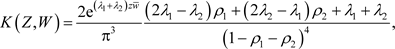 (2.2)
(2.2)
其中
由定理2.1,我们得到以下结论。
定理2.2. 在定理2.1的假设下,则域D的Bergman核
在
上有零点的充要条件是
。
3. 定理2.1的证明
证明. 记
这里
,
表示D上解析函数全体,
表示Lebesgue测度。对于包含原点的Reinhardt域D上的全纯函数f,在D上有幂级数展开式(见 [1] )
这里
容易直接证明
是Reinhardt域上的一组规范正交系,可以证明它是完备的。因而有
其中
直接计算得

上面用到
以及

这里用到

所以当
时
这里
。
由于
于是有
记
这里
根据
得
因此
证毕
4. 定理2.2的证明
为了研究定理2.1中域D的陆启铿问题,我们先给出以下结论。
定理4.1. 在定理2.1的条件下,以下结论成立:
(i) 如果
,那么
(4.1)
(ii) 如果
和
,则存在
,使得
和
。
证明. (i) 由于
同样得
其中
于是由不等式
得
再根据
得
同样得
(ii) 令
,则
,并且
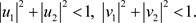
如果
和
至少有一个为零,则结论成立。以下假定
,并证明关于
的不等式组
(4.2)
有解。
令
,则上面不等式组(4.2)等价于
进一步化简得
于是不等式组(4.2)有解等价于不等式组
有解。容易验证当
时,
是它的解。证毕
现在给出定理2.2的证明。
定理2.2的证明。(i) 当
时,有
因
所以
(ii) 当
时,有
由此得
(iii) 当
时,如果
,根据(2.2)有
(4.3)
令
,则
根据
得不等式组
(4.4)
关于
有解。
记
则
的解为
的解为
(iii-1) 当
时,令
的解为
的解为
此时不等式
的解为
不等式
的解为
这表明不等式组(4.4)有解
当
时,有
,根据定理4.1得
在
内有解。
(iii-2) 当
时,如果不等式组(4.4)有解,则
不可能是(4.4)的解,这是因为
于是解
满足以下条件
(4.5)
这里
由(4.5)可知
这等价于
进一步化简得
这和条件
矛盾。因此在
时,对一切
,Bergman核
。证毕
致谢
大学生创新创业训练计划项目(No: S202210649222)。
NOTES
*通讯作者。