1. 引言
函数方程的稳定性问题起源于Ulam [1] 在某一次数学研讨会上提出的度量群中群同态稳定性的问题。一年后,在Banach空间的假设条件下,Hyers [2] 对Ulam关于可加性映射的问题给出了一个肯定的答复,得到了关于柯西函数方程稳定性问题的第一个定理,即:假设A和B都是Banach空间,对于任意的
和
,映射
满足:
则存在唯一的可加映射
使得
随后,Aoki [3] 将Hyers定理推广到了可加映射。1978年,Rassias [4] 对Hyers方法中控制条件进行了减弱,换成了
,在此基础上研究了线性映射的稳定性。进一步地,Găvruta [5] 对Rassias定理中的
替换成更一般的控制函数形式
,得到了更一般的结果。这一结果后来有大量的推广形式,统称为函数方程的Hyers-Ulam-Rassias稳定性。此后,许多学者研究了不同空间下不同函数方程的Hyers-Ulam-Rassias稳定性(可见参考文献 [6] [7] [8] )。
1996年,Isac和Rassias [9] 首次利用不动点定理来证明函数方程的稳定性,使得证明过程更简洁化,后称为不动点法。通过利用不动点法,许多学者对多种函数方程的稳定性进行了深入研究,相关内容可参考书籍 [10] 。
Katsaras [11] 首先在向量空间上定义了模糊范数以及构建了一个模糊拓扑结构。然后,Bag和Samanta [12] 给出了模糊范数的概念并研究了模糊赋范空间的各种性质。在1996年,Jun和Park [13] 研究了导子在Banach代数上的Hyers-Ulam-Rassias稳定性。Badora [14] 在2002年证明了Banach代数上环同态和环导子的稳定性。进一步地,Gordji [15] 研究了环同态和环导子在模糊Banach代数上的稳定性。在2009年,Mirmostafaee [16] 给出了模糊连续的定义,并证明了四次函数方程在模糊赋范空间的连续性。
在 [17] 中,作者提出了高环同态的定义,即:
设
是Banach代数,实数
,从
到
的映射所组成的序列为
。如果对所有的
和所有的正整数n,有
和
则称
是一个高环同态。
本论文组织如下:第二节的内容是本篇论文所涉及到的基础概念和不动点定理。第三节的内容是证明了高环同态在Banach代数上的模糊稳定性和模糊连续性,以及关于这两个定理的推论。第四节是本篇论文的总结。
2. 预备知识
本节将介绍本篇论文所涉及到的一些基础概念,其中
,
,
分别代表实数域,有理数域,自然数集。
定义2.1:设
既是一个代数,又是一个赋范线性空间,且对
,满足
则称
是赋范代数。
定义2.2:设X是一个非空集合,如果对任意的
,集合X上的函数
满足:
1)
当且仅当
;
2)
;
3)
,
则称d为广义度量,为
广义度量空间。
定义2.3 [8] [12] 设X是实线性空间,函数
,如果对任意的
和任意的
,函数N满足:
(N1) 对
,有
;
(N2) 对任意的
,
当且仅当
;
(N3) 若
,则
;
(N4)
;
(N5)
在实数域上是非减函数且
;
(N6) 对
,
在实数域上是(上半)连续的,
则称
为模糊赋范线性空间。
例子2.4:设
是赋范线性空间,则
是X上的模糊范数。
证明:显然满足定义2.4的(N1),(N2),(N5)和(N6)。下面我们验证(N3)和(N4)。
令常数
,当
时,有
,故(N3)成立。当
时,对任意的
有
故
是模糊范数。
定义2.5 [11] [12] 设
是模糊赋范线性空间,
是X中的一个序列。如果在X中存在一个x使得对任意的
时有
,则称序列
是收敛的。我们将其记作
。
定义2.6 [8] [12] 设
是X中的一个序列。如果对每一个
和
,存在
使得对任意的
和
,有
,则称序列
是柯西序列的。若模糊赋范线性空间中每个柯西序列都是收敛的,则这个模糊范数是完备的,并将该空间称为模糊Banach空间。
定义2.7 [14] 设
是模糊赋范空间,函数
且
,如果对任意的
有某个
,当
时,有
,则称f为α-模糊连续。若
对每个
都α-模糊连续,则称f为模糊连续。
定义2.8 [8] 设X是代数,
是模糊赋范空间。如果对
和
,有
则称
是模糊赋范代数。此外,完备的模糊赋范代数被称为模糊Banach代数。
引理2.9 [17] (不动点定理) 设
是广义完备度量空间,
是严格压缩映射,即对某些常数
和
,有
那么,对X中一个给定的元素x,要么对所有的非负整数n有
成立,要么存在一个正整数
使得
1) 当
时,有
;
2) 设J的不动点为
,则序列
收敛到
;
3)
是J的唯一不动点且
;
4) 对所有的
,有
。
3. 主要结果
在本节中,通过采取不动点的方法研究高环同态在模糊Banach代数上的Hyers-Ulam-Rassias稳定性以及模糊连续性。
定理3.1:设
是模糊(复) Banach代数,实数
假设
和
是由函数所组成的序列,且存在常数
使得对每个
和任意的
,有
(1)
与
(2)
如果从
到
的映射所组成的序列为
(n为正整数)满足
,且对
和
,有
(3)
和
(4)
成立,则存在唯一的高环同态
使得对每个正整数n和
,有
(5)
证明:令(3)中
,则根据(N3),当
和
时,有
(6)
设正整数n是固定的。定义集合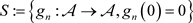 和广义距离
为
和广义距离
为
显然
是完备的广义度量空间 (证明见参考文献 [18] )。定义映射
为
其中
。令
,且存在某个
,使得
。因为
所以
于是,可得J是压缩映射。下面证明
。
根据(6),可得
即
故可得
,满足引理2.10的条件,从而有:
i) 设
,则
是J的唯一不动点,其中
ii)
收敛到
,可定义
为
其中 。
。
iii)
。根据距离的定义,可得
下面证明
满足定义2.3的两个方程。首先,对(1)作归纳假设得:
显然
时,(1)是成立的。假设
时假设成立,验证
时,有
故假设成立。同理,类似可得
其次,在(3)中,用
,
分别替代x和y,得
因为当
时,
,所以
(7)
最后,利用定义2.4的(N4),得
由(N5)可得:对
和
,有
。由(7)可得
通过模糊范数的定义可知
(8)
其中
。因此,
满足可加性。在(4)中,用
,
分别替代x和y,得
因为当
时,
,所以
(9)
结合(N4)和(9)得
故
,其中
。证毕。
下面给出由定理3.1所得到的两个推论。
推论3.2:设
是模糊(复) Banach代数,实数
。假设
和
是由函数所组成的序列,且存在常数
使得对每个
和所有的
,有
与
如果从
到
的映射所组成的序列为
(n为正整数)满足
,且对
和
,有
和
成立,则存在唯一的高环同态
使得对每个正整数n和
,有
证明:根据定理3.1的证明,类似考虑完备广义度量空间
和压缩映射J,并定义J为
令
,存在某个
,使得
。因为
所以
故J是压缩映射。由(6)可得
故
。于是对
和
,利用不动点方法,有
和
剩余部分证明与定理3.1类似。证毕。
推论3.3:设
是模糊(复) Banach代数,实数
和
。假设由函数所组成的序列
和
,且当
时
;当
时
。如果从
到
的映射所组成的序列为
(n为正整数)满足
,且对
和
,有
和
成立,则存在唯一的高环同态
使得对每个正整数n和
,有
证明:根据定理3.1的证明,令
和
。采取相同方法,选取
,
分别为
和
,可证得该推论。
下面将研究高环同态在Banach代数上的模糊连续性。假设定理3.1是成立的,并使用定理3.1中的术语。
定理3.4:若对任意的
,从
的映射
是模糊连续的和从
的映射
是模糊连续的,则映射
也是模糊连续的。
证明:固定
,可得:
,使得
于是,根据(5)和
,利用
的可加性,推得
因为映射
和
是模糊连续的,所以存在
,使得当
时,有
和
于是,可得
故而
因此,结合定义2.8就可证得映射
也是模糊连续的。
推论3.5:在定理3.4满足的情况下,对任意的
和
,有
成立。
证明:在式(8)中,设k为正整数。令
,得
,所以
时是成立的。
又令
,则
所以
时是成立的。现用数学归纳法,假设
时是成立的,我们证明当
时,
也是成立的。我们令
,则
所以
时也是成立的。设
,则
故对任意的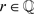 有
。令
,则存在一个有理数列
使得
。又
有
。令
,则存在一个有理数列
使得
。又
因为
的连续性,所以有
成立。
4. 总结
本文通过利用不动点定理,结合模糊范数的定义与性质,证明了在模糊Banach代数上高环同态的Hyers-Ulam-Rassias稳定性。通过改变控制函数的条件和控制函数的形式,得到了两个推论。此外,我们结合模糊连续的定义,证得了高环同态的模糊连续性。这一结果对于后续研究其它同态在模糊Banach代数上的稳定性和连续性有一定的借鉴作用。
致谢
感谢匿名审稿人的宝贵修改建议,这些大大提高了论文的发表。本论文得到了国家自然科学基金(No. 12061018)的资助。
NOTES
*通讯作者。