基于HPM视角下的“等差数列”教学探究

Research on Arithmetic Series Teaching Based on HPM Perspective

摘要: HPM是数学教育的重要学术研究领域之一，运用多种方式将数学史融入教学也具有重要意义。本文将在HPM视角下，探究等差数列的数学史料，并将数学史融入课堂教学。

Abstract: HPM is one of the important academic research fields of mathematics education, and it is also of great significance to integrate the history of mathematics into teaching in various ways. This paper will explore the mathematical historical data of arithmetic series from the perspective of HPM, and integrate the history of mathematics into classroom teaching.

1. 关于HPM

1972年，在第二届国际数学教育大会，组织成立了数学史与数学教学关系国际研究小组(简称HPM)，并于1976年正式隶属于国际数学教育委员会(ICMI)，现在我们通常也将数学史与数学教育关系这一学术领域本身简称为HPM [1] ，自此，HPM开始成为重要学术研究领域之一。汪晓勤教授作为我国HPM领域的著名学者，曾在其著作《HPM：数学史与数学教育》中提出运用数学史的教学实践方法有附加式、复制式、顺应式和重构式。附加式通过展示有关的数学家图片、讲述趣闻轶事等，去掉与否对内容无影响；复制式是直接采用历史上的问题、解法等；顺应式是根据历史材料编制数学问题；重构式是借鉴或重构知识的发生、发展历史 [2] 。

2. 等差数列的数学史料

2.1. 等差数列的源起

数列的历史悠久，而等差数列是数学历史上最早出现的数列之一。在公元前1650年，古埃及的莱茵德纸草书中记载的粮食分配问题；在我国，公元前2世纪的楚国铜环权的重量分布特点 [3] ；古巴比伦泥板上的分银问题；中国《九章算术》中的织布问题；《张丘建算经》中的赐金问题等都涉及了等差数列 [1] 。由此可见，等差数列的数学历史源远流长，并且受到国内外数学家的广泛重视和研究。

2.2. 等差数列的展现

2.2.1. 天坛之板

北京天坛始建于明永乐十八年(1420年)，清乾隆年间最终建成，是明、清两代帝王祭祀皇天、祈五谷丰登的场所。天坛分为圜丘坛和祈谷坛，是建筑和景观设计的杰出代表，朴素而鲜明地体现出对世界伟大文明之一的中国发展产生过影响的一种极其重要的宇宙观 [4] 。其中，圜丘坛的地面由石板铺成，最中间是天心石，围绕天心石的是9圈圆扇环形的石板，从内到外的石板数为9，18，27，36，45，54，63，72，81 [5] 。

2.2.2. 引入函数

1931年，数学家Smail在其编写的教科书《College Algebra》中，在“一元线性函数”这一章中将等差数列作为其中的一小节，即将等差数列与函数相联系，用函数观点看等差数列。对于任意的一次函数 $y=ax+b$ ，x依次取值0, 1, 2, 3, ∙∙∙时，得到一系列对应的函数值 $b,a+b,2a+b,3a+b,\cdots$ ，相邻两项之差为a，这样一组数即为等差数列 [6] 。

2.3. 等差数列的题目

《九章算术》中一题“今有金箠，长五尺。斩本一尺，重四斤。斩末一尺，重二斤。问：次一尺各重几何 [1] ？”翻译为“现有一根金箠，长五尺，一头粗，一头细，在粗的一端截下1尺，重4斤；在细的一端截下1尺，重2斤；问依次每一尺各重多少斤？”

2.4. 等差数列的故事

棣美弗(A. De Moivre, 1667~1754)是法国数学家，主要研究三角学和概率论，有许多论文著作以及社会荣誉 [1] ，同时也是牛顿的亲友。

棣美弗死亡也是充满数学色彩的。在去世前不久，他声称以后每天比前一天多睡15分钟，而在睡满24小时那天也迎来了他生命的终点。由此可改编为一道等差数列的数学习题：棣美弗当年9月24日的睡眠时间是8小时，根据史料记载，他去世于当年的11月27日，根据以上叙述，棣美弗总共睡了多久？

3. HPM视角下的“等差数列”教学设计

等差数列

【教学内容】人教版高中数学选择性必修二12页等差数列

【教学理念】

1. 运用重构式设计“数学史 + 问题链”的整体教学结构，还原数学知识的产生历程、文化背景和历史发展，转化知识形态，基于教材内容和客观现实 [7] ，帮助学生实现数学知识的“再创造”。

2. 在教学设计环节中运用附加式、复制式以及顺应式，将数学史融入等差数列的课堂教学之中，渗透数学文化，激发学生学习兴趣，加深学生对于数学的理解，培养学生爱国情怀，提升学生的价值观和数学学科素养。

【教学目标】

1. 理解并掌握等差数列的定义、通项公式以及相关性质。

2. 经历等差数列数学表示的过程，能够灵活运用所学知识，解答实际问题。

3. 激发学习兴趣，感悟数学文化，揭示数学发展与人类文明发展之间的联系，培育数学观并提升数学核心素养。

【教学重难点】

教学重点：理解并掌握等差数列的定义、通项公式以及相关性质。

教学难点：等差数列通项公式的推导以及应用。

【教学过程】

(一) 引入

教师提问学生是否参观过北京天坛以及注意过其地面的石板数引入，而后加入上述2.2.1天坛之板的材料。

教师提出天坛从内到外的石板数：第1圈是9，第2圈是18，第3圈是27，第4圈是36，第5圈是45，第6圈是54，第7圈是63，第8圈是72，第9圈是81。引导学生自主思考并发现其中规律，追问：若有第10圈石板，那么其石板数应为多少？

生：应为90。因为这些石板数前一个与后一个之间都相差9，所以第10圈的石板数为81 + 9 = 90。

教师初步小结：天坛从内到外的石板数组成了一个数列，且该数列的前一项与后一项之间的差是9。并依次给出自然数数列、奇数数列和偶数数列，再次提问学生其数列特点。

自然数数列：0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 ∙∙∙

生：自然数数列的前一项与后一项之间的差是1。

奇数数列：1, 3, 5, 7, 9, 11, 13 ∙∙∙

生：奇数数列的前一项与后一项之间的差是2。

偶数数列：2, 4, 6, 8, 10, 12, 14 ∙∙∙

生：偶数数列的前一项与后一项之间的差是2。

教师总结：以上数列的前一项与后一项之间的差都是定值，这样特殊的数列是什么数列呢？这样的数列又有哪些特点和性质呢？让我们共同走进本节课的学习。

设计意图：引入部分运用了顺应式，向学生介绍北京天坛圜丘坛排列的石板，进行假设并提问学生第10圈的石板数，并提及学生常见的自然数和奇偶数数列，从而根据这些表象引导学生思考并发现这些数列的特点，从而引入本节等差数列教学。

(二) 课程新授

1. 等差数列的定义

一般地，如果一个数列从第2项起，每一项与它的前一项的差都等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母d表示。

我们知道由三个数 $a,A,b$ 组成的等差数列可以看成是最简单的等差数列。这时，A叫做a和b的等差中项，根据等差数列的定义可知 $2A=a+b$ 。

教师提问上述提到的数列是否为等差数列并判断其公差。

生：上述数列都是等差数列，石板数所组成的数列公差是9，自然数数列的公差是1，奇数数列和偶数数列的公差都是2。

初步学习等差数列概念后，加入上述2.1等差数列的源起相关材料，并强调我国数学家的坚持探索与深入研究，树立榜样，努力学习数学。

2. 等差数列的通项公式

内容： $a_n=a_1+\left(n-1\right)d,\left(n\ge 2\right)$

教师提出设一个等差数列 $\left\{a_n\right\}$ 的首项为a₁，公差为d。提问能否得出关系式并尝试猜想等差数列的通项公式，并组织学生小组讨论。

生1：根据等差数列的定义，可以得到 $a_2-a_1=d,a_3-a_2=d,a_4-a_3=d,\cdots$ 。

生2：根据等差数列的定义，可以得到 $a_{n+1}-a_n=d$ 。

师生共同尝试推导并猜测等差数列的通项公式。

$a_2=a_1+d$ ，

$a_3=a_2+d=\left(a_1+d\right)+d=a_1+2d$ ，

$a_4=a_3+d=\left(a_1+2d\right)+d=a_1+3d$ ，

$\cdots$

可以猜测 $a_n=a_1+\left(n-1\right)d,\left(n\ge 2\right)$ 。

接下来教师讲解等差数列通项公式的证明：

① 迭代法：

$a_n=a_{n-1}+d=\left(a_{n-2}+d\right)+d=\left(\left(a_{n-3}+d\right)+d\right)+d=\cdots =a_1+\left(n-1\right)d$

② 裂项相消法：

$a_n=a_1+\left(a_2-a_1\right)+\left(a_3-a_2\right)+\left(a_4-a_3\right)\cdots +\left(a_n-a_{n-1}\right)=a_1+\left(n-1\right)d$

3. 等差数列与函数

教师引导学生发现等差数列的通项公式与一次函数的表达式相像，并组织学生小组合作尝试将等差数列的通项公式展现在函数图像中。

学生讨论结束，分享想法和所作图像，见图1。

完成探究等差数列通项公式与函数关系后，加入上述2.2.2引入函数的内容。

设计意图：课程新授部分运用了附加式，教师在给出等差数列的定义之后，接下来便着重介绍了等差数列在我国的发展历史，帮助学生加深对于等差数列的认识和理解，同时让学生体悟等差数列的数学历史和文化，并培养学生的爱国情怀；并且，教师在讲解等差数列与函数关系的内容之后，也向学生们介绍了以前的数学家们是如何将等差数列与函数相联系的，提升学生的数学文化素养和内涵，不再局限于教材上系统化的数学知识，并且丰富和拓展了等差数列的教学内容。

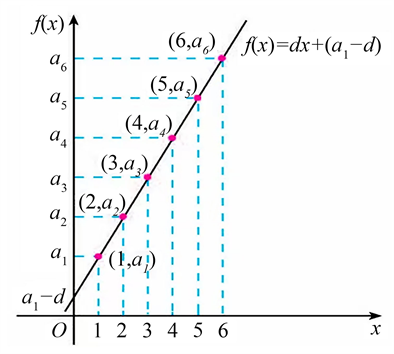
Figure 1. Function image of arithmetic sequence pass-term formula

图1. 等差数列通项公式的函数图像

(三) 小试身手

(《九章算术》)“今有金箠，长五尺。斩本一尺，重四斤。斩末一尺，重二斤。问：次一尺各重几何？”

师生共同讨论，翻译出题意：

(《九章算术》)“现有一根金箠，长五尺，一头粗，一头细，在粗的一端截下1尺，重4斤；在细的一端截下1尺，重2斤；问依次每一尺各重多少斤？”

生：根据题意，设 $a_1=4$ ， $a_5=2$ ，则有 $a_5-a_1=2-4=-2=4d$ ，解得 $d=-\frac{1}{2}$ ，由此可以解得 $a_2=\frac{7}{2},a_3=3,a_4=\frac{5}{2}$ 。

设计意图：小试身手部分运用了复制式，教师在讲解完等差数列的主要内容后，加入《九章算术》中的原题，组织学生小组讨论，共同翻译得出题意，并引导学生尝试通过自己的努力运用本节所学知识解答题目，陶冶学生的数学文化情操，增添学生自身的成就感，加强学生学习的主动性和课堂参与感，锻炼学生对于本节课等差数列知识的掌握和应用。

(四) 思考提升

课堂接近尾声，教师总结本节课重点并给出上述2.4等差数列的故事的相关材料，提问学生解题方法。由于本节课所学知识有限，教师为下节课等差数列的前n项和埋下伏笔。

教师留下课后思考：是否存在数学公式或定理能够直接根据已知求出数列的项数总和？同学们自行思考，下节课会给出答案。

设计意图：思考提升部分运用了顺应式，根据数学家棣美弗生命之限的故事，改编为一道等差数列习题，吸引学生兴趣的同时，也留给学生更多提升和思考的空间，并为下节课等差数列的前n项和埋下伏笔。

【板书设计】见图2。

Figure 2. Blackboard design

图2. 板书设计

【教学反思】

本次教学设计紧紧围绕将数学史以附加式、复制式、顺应式和重构式的方式融入等差数列的教学之中，立足于HPM视角进行等差数列的教学设计，能够激发学生的数学学习兴趣，加深其对于数学的理解，并进行思政建设，培养学生的爱国情怀与积极奋进的优秀品质。也存在不足之处，数学史料的融入应注意适度，把握课堂教学的重点与进度。

4. 结语

HPM愈发受到人们的关注与研究，基于HPM视角进行高中数学教学探究也是十分具有研究意义，通过将数学史融入教学，学生能够更深入清晰地了解数学知识的发生发展过程以及涉及到的规律方法，感受数学深厚的历史文化魅力，并加强学生的思政建设，培养学生的数学学习兴趣与爱国情怀，提升学生的数学核心素养。因此，本文重点基于HPM视角下进行等差数列的史料研究与教学设计，希望能为一线教师以及教育工作者们提供一些教学材料与研究思路，本文也存在一些不足之处，笔者也会继续改进与完善。