形式三角矩阵环上的相对强Gorenstein投射模
Relative Strongly Gorenstein ProjectiveModules over Formal TriangularMatrix Rings
DOI: 10.12677/PM.2024.141011, PDF,   
作者: 张会晶：西北师范大学，数学与统计学院，甘肃 兰州
关键词: 形式三角矩阵环；相对强 Gorenstein 投射模；Formal Triangular Matrix Ring； Relative Strongly Gorenstein Projective Module
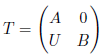
摘要: 设是形式三角矩阵环，其中 A,B是环，U是(B,A)-双模。本文描述了某些情况下，T上的相对强 Gorenstein 投射模的结构。
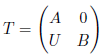
Abstract: Let be a formal triangular matrix ring, where A and B are rings and U is (B,A)bimodule. In this paper, we characterize the structure of relative strongly Gorenstein projective modules over T under some conditions.
文章引用：张会晶. 形式三角矩阵环上的相对强Gorenstein投射模[J]. 理论数学, 2024, 14(1): 94-103. https://doi.org/10.12677/PM.2024.141011

参考文献

[1] Enochs, E.E. and Jenda, O.M.G. (2000) Relative Homological Algebra. Walter de Gruyter, Berlin.
https://doi.org/10.1515/9783110803662
[2] Zhang, P. (2013) Gorenstein Projective Modules and Symmetric Recollements. Journal of Algebra, 388, 65-80.
https://doi.org/10.1016/j.jalgebra.2013.05.008
[3] Mao, L.X. (2020) Cotorsion Pairs and Approximation Class over Formal Triangular Matrix Rings. Journal of Pure and Applied Algebra, 224, 106271-106292.
https://doi.org/10.1016/j.jpaa.2019.106271
[4] Bennis, D., Maaouy, R.E., Rozas, J.R.G. and Oyonarte, L. (2021) Relative Gorenstein Dimen- sions over Triangular Matrix Rings. Mathematics, 9, Article 2676.
https://doi.org/10.3390/math9212676
[5] Holm, H. (2004) Gorenstein Homological Dimensions. Journal of Pure and Applied Algebra, 189, 167-194.
https://doi.org/10.1016/j.jpaa.2003.11.007
[6] Bennis, D., Rozas, J.R.G. and Oyonarte, L. (2016) Relative Gorenstein Dimensions. Mediter- ranean Journal of Mathematics, 13, 65-91.
https://doi.org/10.1007/s00009-014-0489-8
[7] Bennis, D. and Mahdou, N. (2007) Strongly Gorenstein Projective, Injective and Flat Modules. Journal of Pure and Applied Algebra, 210, 437-445.
https://doi.org/10.1016/j.jpaa.2006.10.010
[8] Bennis, D., Maaouy, R.E., Garca Rozas, J.R. and Oyonarte, L. (2021) Relative Gorenstein Dimensions over Triangular Matrix Rings. Mathematics, 9, Article 2676.
https://doi.org/10.3390/math9212676
[9] Haghany, A. and Varadarajan, K. (2000) Study of Modules over Formal Triangular Matrix Rings. Journal of Pure and Applied Algebra, 147, 41-58.
https://doi.org/10.1016/S0022-4049(98)00129-7

为你推荐