基于贝叶斯优化的卷积神经网络结合机器学习分类器的滑坡易发性预测研究

Landslide Susceptibility Prediction Based on Bayesian Optimization Convolutional Neural Network Combined with Machine Learning Classifier

摘要: 现有使用机器学习进行滑坡监测方法存在滑坡易发性特征选择超参数多为连续变量，数值约束松散的问题。为解决此问题，提出一种结合CNN-LR-SVM的滑坡易发性监测方法。使用CNN提取滑坡易发性特征值，捕获输入数据中的上下文信息，消除繁琐的传统特征选择过程，提升特征选择准确率。将提取到的特征值与LR、SVM分类器结合。之后，使用贝叶斯优化方法寻找CNN、LR和SVM超参数，考虑历史信息，优化下一步超参数设置方法，解决超参数优化数值约束问题。经实验验证，本方法在选择不同优化算法与激活函数时相比传统单一机器学习模型(以CNN与SVM为例)均有良好性能表现。

Abstract: The existing landslide monitoring methods using machine learning have the problem that most of` the hyperparameters selected for landslide susceptibility characteristics are continuous variables and the numerical constraints are loose. To solve this problem, a landslide susceptibility monitoring method combined with CNN-LR-SVM is proposed. Using CNN to extract landslide prone feature val-ues, capture context information in input data, eliminate complicated traditional feature selection processes, and improve feature selection accuracy. The extracted eigenvalues are combined with LR and SVM classifiers. Then, using the Bayesian optimization method to find CNN, LR and SVM hyperparameters, considering the historical information, the next step of the hyperparameter setting method is optimized to solve the numerical constraint problem of hyperparameter optimization. The experimental results show that the proposed method has good performance compared with the traditional single machine learning model (take CNN and SVM as examples) when selecting different optimization algorithms and activation functions.

1. 引言

滑坡是物质在重力作用下的下坡运动，是一种常见的地质灾害现象，会造成大量人员伤亡及财产损失。因此，确定滑坡易发区是预防和减少潜在损害的有效手段。滑坡易发性是根据给定数据预测地区是否易发生滑坡。近年来，滑坡易发性预测引入了各种机器学习方法 ‎[1] ，这些方法包括决策树、逻辑回归、支持向量机、随机森林和人工神经网络等。特征选择是一种常用的特征工程技术，用于去除不相关和冗余的滑坡诱发因素 ‎[2] 。现有特征选择方法有粗糙集理论、基于卡方的特征选择方法、贡献值排序和极限学习机等。此外，还采用了其他特征选择技术，如信息增益比、基于相关性的方法和relief-F等。

然而，现有滑坡监测技术存在一些问题 ‎[3] 。首先，不同的特征选择方法可能会导致不同的敏感性分析结果，选择不合适的特征选择方法可能会产生负面影响。其次，选择最重要的滑坡诱发因子的标准仍存在争议，缺乏一致性的选择标准 ‎[4] 。最后，现有滑坡易发性特征选择超参数多为连续变量，数值约束松散，影响滑坡易发性预测准确率。

2. 应用机器学习进行滑坡监测现有研究分析

2.1. 支持向量机

Table 1. Kernel functions are commonly used in support vector machines

表1. 支持向量机常用核函数

支持向量机(SVM)基于结构风险最小化，使用核函数隐式将数据映射到高维特征空间，支持向量机使用“核技巧”有效地执行非线性分类 ‎[5] ，隐式地将输入映射到高纬特征空间，如表1所示。

定义训练数据集，其中，当数据是线性可分时，得到可分离地超平面如公式(1)所示，

$y_i\left(w\cdot x_i+b\right)\ge 1-{\delta }_i$ (1)

其中，w是定义超平面空间在特征空间地方向系数向量，b是超平面与元代你的偏移量， ${\delta }_i$ 是正松弛变量。用于新数据分类的决策函数如(2) (3)所示，

$g\left(x\right)=sign\left({\displaystyle {\sum }_{i\ast 1}^n{y}_i{\alpha }_j{x}_i}+b\right)$ (2)

$g\left(x\right)=sign\left({\displaystyle {\sum }_{i\ast 1}^n{y}_i{\alpha }_{j}K\left(x_i,x_j\right)}+b\right)$ (3)

其中，α是拉格朗日乘子，当无法使用线性函数分离超平面时，可使用一定的非线性核函数将原始输入数据转移到高维特征空间中 ‎[6] ，此时如公式所示，其中 $K\left(x_i,x_j\right)$ 是核函数。

2.2. 逻辑回归

逻辑回归(LR)是一种多元统计方法，使用逻辑函数对二元因变量建模，首先将每个滑坡特征变量作为一个逻辑变量 ‎[7] ，之后利用最大似然估计得到其概率，逻辑回归模型公式如(4)所示，

$p=\frac{1}{1+{\text{e}}^{-z}}$ (4)

其中，p为概率，z为一组变量的线性组合。Z如(5)所示，其中 ${\alpha }_0$ 为模型截距，( ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N$ )为表示( $X_1,X_2,\cdots ,X_N$ )影响的回归系数。

$z={\alpha }_0+{\alpha }_1{X}_1+{\alpha }_2{X}_2+\cdots +{\alpha }_N{X}_N$ (5)

2.3. CNN

Figure 1. CNN extracted landslide eigenvalue architecture diagram

图1. CNN提取滑坡特征值架构图

与传统神经网路不同，CNN是一种受生物学启发的深度学习技术，在特征提取方面表现出强大的能力 ‎[8] 。在滑坡易发性研究中，首先将滑坡诱发因素叠加在一起 ‎[9] ，把整个研究区域看作一个“多通道图像”，每个因子代表一个通道 ‎[10] ，最终对这个“图像”中的每个像素进行分类 ‎[11] ，第一步要先构造出一个纯CNN架构，如图1所示，输入层由多个神经元组成 ‎[12] ，每个神经元代表一个滑坡诱发因子。

Figure 2. CNN processing renderings

图2. CNN处理效果图

CNN架构中特殊的卷积处理可以利用一组卷积核捕获滑坡特征向量之间的局部表示 ‎[9] ，卷积操作如(6) (7)所示 ‎[13] ：

$C_j={\displaystyle {\sum }_i^{N}f}\left(w_j\ast v_i+b_j\right),j=1,2,3,\cdots ,k$ (6)

$f\left(x\right)=\tanh \left(x\right)=\frac{{\text{e}}^x-{\text{e}}^{-x}}{{\text{e}}^x+{\text{e}}^{-x}}$ (7)

其中， $v=\left\{v_1{v}_2\cdots v_N\right\}$ 为输入滑坡数据，其中N为诱发因素个数， $f\left(x\right)$ 是非线性激活函数，*为卷积算子 ‎[14] ，k为卷积核数， $w_j$ 和 $b_j$ 分别为权重和偏置 ‎[10] 。

池化操作通过将前一层N−1个输出组合成下一层的单个值来减少特征向量的大小。每个池化层不同寻常地遵循前一个卷积层 ‎[15] 。在整个研究中使用了广泛使用的最大池化操作，计算方式如(8)所示：

$a_j={\max }_{n\ast 1}\left(a_j^{n\ast 1}u\left(n,1\right)\right)$ (8)

其中， $u\left(n,1\right)$ 的窗函数， $a_j^{n\ast 1}$ 为最大值。之后，这些由卷积和池化操作提取的局部表示通过完全连接层进行重组 ‎[16] 。最后，将完全连接层连接到输出层，输出层由两个代表滑坡和非滑坡的神经元组成 ‎[11] 。CNN层的所有参数都使用反向传播算法进行优化，从而使损失函数计算出的计算值最好 ‎[13] ，损失函数如(9)所示：

$Loss=-\frac{1}{m}{\displaystyle {\sum }_{i=1}^m\left[y_i\log \left(\overline{y_i}\right)+\left(1-y_i\right)\log \left(\overline{1-y_i}\right)\right]}$ (9)

其中，m为输入滑坡数据个数， $y_i$ 和 $\overline{y_i}$ 两个变量分别表示第i个输入样本的真实标签和预测标签 ‎[12] 。

迭代更新参数，知道损失函数收敛，CNN处理效果图如图2所示。

3. 基于CNN-LR-SVM结合模型的滑坡监测结合模型

3.1. 滑坡诱发因子筛选

Table 2. Landslide inducing factor

表2. 滑坡诱发因素

滑坡是由多种原因导致，这些原因成为滑坡诱发因素，选择合适的因子对建立可靠的滑坡易发性模型具有重要意义。海拔高度是决定边坡应力分布、岩石风化程度的关键因素之一。坡度决定了水的辐合和辐散，从而影响了边坡的稳定性。坡向受太阳辐射和降水影响，反映了地形表面最大坡度的方位或方向。剖面率是垂直平面上与坡向平行的曲率，体现了地形的复杂性，而平面曲率是影响地表径流特征的另一种曲率，代表了沿着曲线的微小弧线的斜率变化，影响了斜率的不稳定性。归一化植被指数(NDVI)定量反映植被覆盖度和生长情况。岩性描述了地质工程特征。距离相关因素影响山体滑坡的蔓延和规模，包括与断层、道路和河流的距离因素。

水文因素是滑坡影响要素的另一个关键因素，包括输沙指数(STI)、河流动力指数(SPI)、地形粗糙度指数(TRI)和地形湿度指数(TWI)。STI用于定性解释侵蚀和沉积过程，公式如(10)所示：

$\text{STI}=A_S\ast \tan \propto$ (10)

其中，A_s为特定集水区面积， $\propto$ 为坡角。STI用于描述重力作用域沉积物时强颗粒的运动，公式如(11)所示：

$\text{SPI}={\left(\frac{A_S}{\alpha }\right)}^x\ast {\left(\frac{\sin \propto }{\beta }\right)}^Y$ (11)

河流动力指数(SPT)可以体现河流动力程度。地形湿度指数(TWI)用于计算地形湿度，地形粗糙指数(TRI)用于计算地形粗糙程度，公式如(12) (13)所示：

$\text{TRI}=\sqrt{{\max }^2-{\min }^2}$ (12)

$\text{TWI}=\ln \left\{\frac{A_s}{\propto }\right\}$ (12)

其中，max和min为DTM 9个矩形窗单元的最大值和最小值。具体集水区面积为单位轮廓长度的上坡面积，取单元数乘以网格单元大小。考虑上述11个条件后诱发因素如表2所示。

3.2. CNN、LR、SVM混合建模

准备好滑坡信息和诱发因素后，构建滑坡建模的训练集和验证集，将CNN和LR与SVM进行混合建模，使用贝叶斯优化超参数，使用验证集进行统计度量。建立一个滑坡易发性预测模型，首先，准备滑坡历史位置和诱发因素。其次，使用CNN-LR-SVM结合模型，使用CNN构建滑坡建模训练集和验证集，提取特征值，将CNN提取到的特征值与LR、SVM分类器相结合并结合。最后，基于贝叶斯方法进行超参数优化，并进行模型与功能两方面效能评估，整体流程图如图3所示。

Figure 3. Overall flow chart

图3. 整体流程图

3.3. 结合CNN与传统机器学习分类器

滑坡易发性制图可使用CNN从输入数据中自动提取有用的特征表示，之后结合SVM、LR分类西输出最终的滑坡预测结果。包括特征提取和分类两个步骤。在特征提取过程中，首先使用原始训练集构造并训练与图1相同的CNN结构。经过训练过程后，可以使用纯CNN进行特征提取。

CNN提取原始滑坡数据发送到经过训练，并从全连通层中输出提取的特征。基于以上操作，生成新的训练集和测试集。随后，使用新的训练和测试数据代替原始数据，使用SVM、RF和LR分类器进行滑坡易感性预测。一般来说，滑坡易感性预测过程可以看作是一个二元分类任务。

传统的机器学习分类器可以有效地识别滑坡位置，预测研究区域内滑坡发生的“位置”及其发生概率。在对整个研究区域的滑坡易感性进行预测后，将这些滑坡易感性输入到GIS环境中，进行滑坡易发性制图，准确生成滑坡易感性图，整体流程图如图4所示。

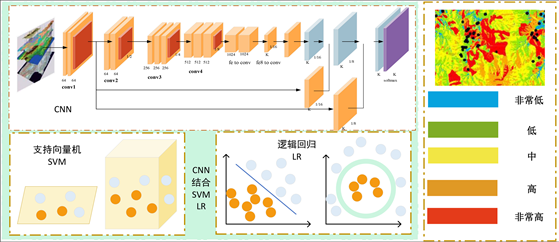
Figure 4. CNN-SVM-LR combined treatment of landslide susceptibility mapping

图4. CNN-SVM-LR结合处理滑坡易发性制图

3.4. 贝叶斯优化超参数选择

Table 3. Hyperparameters and their search space

表3. 超参数及其搜索空间

CNN及其他深度学习技术涉及许多方面超参数优化，包括批处理大小、激活函数、优化算法和隐藏层的数量。大多数超参数是连续变量，对其取值范围只有松散的约束，同时超参数具有耦合效应，所有需要稳定的超参数优化方法，现有优化方法主要包含网格搜索、随机搜索和贝叶斯优化三种，网格搜索对所有可能参数进行优化，当神经网路超参数和搜索空间数量较大时耗时过大；随机搜索选择随机的超参数值，然后评估模型精度，在评估完所有随机数之后，选择最佳的超参数设置，无法保证下一次评估会比之前的设置更好。以上两种方法面临的重要问题就是多次优化迭代忽略了历史信息。

贝叶斯优化基于多次调用方法，每次迭代后找到更好的模型配置，直到第n次调用时收敛，通过优化下一步评估参数设置决策来解决以上问题。当数据量和计算密度较大时，CNN训练会十分耗时，在这种情况下，贝叶斯优化可以快速找到优化后的ANN、SVM、CNN超参数，如表3所示，贝叶斯聚类分析效果如图5所示。

Figure 5. Clustering effect diagram

图5. 聚类效果图

3.5. 模型评价

滑坡易发性模型多采用三个指标评价，总体精度(OA)、马修斯相关系数(Matthews Correlation Coefficient)和卡帕系数(kappa)验证。总体精度根据训练、验证中使用的正确滑坡数量比滑坡总数来计算，总体计算如公式(14) (15) (16)所示：

$\text{Sensitivity}=\frac{TP}{TP+FN}$ (14)

$\text{Specificity}=\frac{TN}{TN+FP}$ (15)

$\text{OA}=\frac{TN+TP}{TP+TN+FP+FN}$ (16)

其中，TN (真阴性)和TP (真阳性)分别表示正确分类的非滑坡和滑坡实例数量，FN (假阴性)和FP (假阳性)分别表示错误分类的滑坡和非滑坡实例的数量。马修斯相关系数是一个介于−1和+1的值，+1表示完美预测，0表示与随机预测效果相同，−1表示预测和观察之间的结果完全不一致，如(17)所示：

$\text{MCC}=\frac{TN\ast TP-FP\ast FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}}$ (17)

Kappa系数是一个用于一致性检验的指标，也可以用于衡量分类的效果。对于分类问题，所谓一致性就是模型预测结果和实际分类结果是否一致。kappa系数计算公式如(18) (19)所示：

$k=\frac{P_C-P_{exp}}{1-P_{exp}}$ (18)

$P_{exp}=\frac{\left(TP+FN\right)\left(TP+FP\right)+\left(FP+TN\right)\left(FN+TN\right)}{\sqrt{TP+TN+FN+FP}}$ (19)

其中， $P_C$ 为正确分类的样本比例， $P_{exp}$ 为变化一致的期望概率。

使用相似性与可分性两个评价标准评估提取特征有效性。类与类之间样本特征差异越大，或同一类样本特征相似性越大，则输入数据越容易被区分。相似性相关系数如(20)所示：

$\rho \left(x_1,x_2\right)=\frac{C\left(x_1,x_2\right)}{\sqrt{D\left(x_1\right)}\sqrt{D\left(x_2\right)}}$ (20)

其中， $x_1$ 和 $x_2$ 是两个特征向量， $C\left(x_1,x_2\right)$ 为协方差矩阵， $D\left(x_1\right)$ 和 $D\left(x_2\right)$ 为两个向量的方差。 Jeffries-Matusita距离是评价两个类之间可分性的可分性指标，如(21) (22)所示：

$J_{ij}=\sqrt{2\left(1-{\text{e}}^{-B_{ij}}\right)}$ (21)

$B_{ij}=\frac{1}{8}{\left(a_i-a_j\right)}^{\text{T}}{\left(\frac{C_i+C_j}{2}\right)}^{-1}\left(a_i-a_j\right)+\frac{1}{2}\log \left(\frac{\left|\frac{C_i+C_j}{2}\right|}{\sqrt{\left|C_i\right|\left|C_j\right|}}\right)$ (22)

其中， $a_i$ 和 $c_i$ 分别为第i类的平均向量和协方差矩阵， $B_{ij}$ 为两类之间的巴氏距离。

4. 实验结果及模型评价

本次实验使用一台具有Core i7-4510U CPU，GeForce RTX 3060 gpu，2.60 GHz，16 GB RAM和x64处理器的计算机上实现。

4.1. 滑坡诱发因子重要性排序

3.1中选用11个滑坡诱发因子，但不能保证所有滑坡诱发因子重要性程度，因此对11个因子进行多重共线性检验及特征重要性分析，在训练完成后计算每个滑坡诱发因子的相对重要性和等级，如表4所示，总结出不同滑坡诱发因子重要值和排序。海拔(重要度 = 1.000)、土壤(重要度 = 0.895)、计划曲率(重要度 = 0.840)是3个最显著的影响因子。3个次要因子分别为地形湿度指数(TWI) (0.521)、坡度(0.512)和滑坡定位(0.347)。此外，根据所有模型的平均验证精度选择最佳子集百分比(8/11)。产率为72.72%，可作为敏感性模型输入。

Table 4. Influence of different landslide inducing factors on the results

表4. 不同滑坡诱发因子对结果影响

4.2. 模型表现

CNN-LR-SVM模型性能评估超过300个epoch并启用早期终止，图6显示了使用训练和验证数据集的81个epoch的模型损失和精度。由于验证精度没有进一步提高，训练在81次后结束。随着时间的推移，训练和验证数据集的模型损失都减少了，这表明模型正在从数据中学习，即CNN-LR-SVM模型学会通过滑坡诱发因子预测滑坡。

同时，随着学习性能的提高，模型训练和验证的准确性也随着时间的推移而增加。模型损失和精度在不同时期的波动可归因于隐藏层的丢失。此外，训练曲线和验证曲线之间的小差距表明过拟合是最小的。

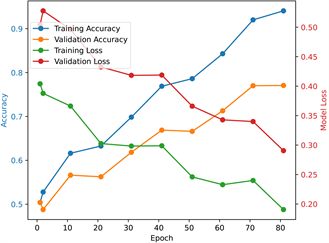
Figure 6. CNN-LR-SVM model performance

图6. CNN-LR-SVM模型表现

4.3. 模型对比分析

图7展示了在不同隐藏层神经元数量、批处理大小和丢包率情况下CNN-LR-SVM模型性能与其他模型(以CNN和SVM为例)进行比较的结果。对模型本身进行分析，可以发现CNN-LR-SVM模型在隐藏层为512、批处理次数为72、丢包率为0.3时取得最好效能。通过构建roc、计算AUROC和5次交叉验证来考察模型的性能。这些发现验证了CNN-LR-SVM在验证和交叉验证数据集上的最高性能。同时可知，在不同隐藏层神经元数量、批处理大小和丢包率情况下，CNN-LR-SVM模型均拥有高于CNN和SVM模型的效能，证明了模型的性能。

Figure 7. Effects of the number of hidden layer neurons, batch size and packet loss rate on the performance of CNN-LR-SVM, SVM and CNN models

图7. 隐藏层神经元数量、批处理大小和丢包率对CNN-LR-SVM、SVM和CNN模型性能的影响

4.4. 选择不同优化算法与激活函数时模型性能对比分析

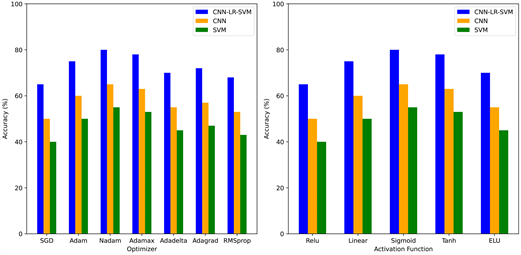
Figure 8. Effects of optimization algorithms and activation functions on the performance of CNN-LR-SVM, SVM and CNN models

图8. 优化算法和激活函数对CNN-LR-SVM、SVM和CNN模型性能的影响

图8显示了优化算法和激活函数对精度的影响。对于人工神经网络和CNN，优化算法和激活类型对验证数据集上的模型精度都有很大影响。经过对比分析，CNN-LR-SVM模型的最佳优化算法与激活函数分别为Nadam和Sigmoid，效果最差的优化算法与激活函数分别为SGD和ReLU。并且通过对结果进行分析可知，在选择不同优化算法与激活函数时，CNN-LR-SVM模型均有超过SVM和CNN的性能表现。

4.5. 贝叶斯优化结果

通过贝叶斯优化选择模型超参数，经过较少的评估，优化运行了25次以找到具有特定搜索空间的最佳参数值。在额外的迭代中没有明显的改进。每次迭代之后，配置总是得到改进。经过25次迭代，找到了最佳模型设置。如图9所示，经过几次迭代，贝叶斯优化取得了较好的效果。为体现模型效果，同时对CNN进行优化。在完成所有评估后，由性能最佳的设置获得的目标函数(即验证精度)的值，CNN-LR-SVM的准确率从72.09%提高到76.20%。

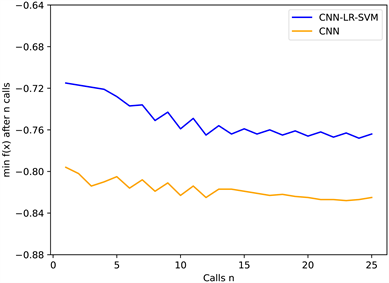
Figure 9. The optimal configuration of ANN and CNN models is obtained by Bayesian optimization

图9. 通过贝叶斯优化得到ANN和CNN模型的最佳配置

4.6. 计算性能

表5总结了模型优化、训练和对新数据进行预测所需的时间(以秒为单位)。通过结果可知优化模型最为消耗时间。在训练时间上，CNN-LR-SVM和CNN的训练时间分别为0.78 s和0.56 s，SVM的训练时间仅为0.09 s。但经上文分析可知CNN-LR-SVM性能强于单一的CNN和SVM模型。本次实验选取一台GeForce RTX 3060gpu机器作为试验机，如果培训规模很大，则可能需要图形处理单元(gpu)或云计算服务，如亚马逊AWS和谷歌云。

Table 5. Model evaluation

表5. 模型评价

5. 结论

本研究使用将CNN提取到的特征值与LR、SVM分类器相结合，使用结合后的CNN-LR-SVM模型，经结果验证，CNN-LR-SVM由于其复杂的架构以及通过卷积和池化操作处理滑坡空间相关性，在处理滑坡易发性预测时性能优于单一的机器学习模型。当结合模型变得复杂时使用较高的丢包率(0.3)以防止过拟合问题。同时，由于CNN包含了许多需要调优的超参数，所以使用贝叶斯优化来搜索它们的最优值。将模型性能与人工神经网络和支持向量机进行比较，验证了模型具有更好的预测率。

参考文献