1. 引言
发放贷款是全球银行的核心业务。巨大的违约损失和激烈的竞争要求金融中介机构准确有效地区分申请人。因此,银行应在申请筛选时决定是否提供信贷。数据主要来自申请表、客户人口统计以及过去借款和还款行为的大量记录。通常,信用评分问题会转化为二元或多类分类。换言之,利用信用数据开发分类器,构建决策支持系统,从而协助银行决定是否向特定申请发放贷款。应用于信用评分的预测模型大致可分为两组:统计方法和人工智能(AI)方法。许多研究都集中在建模方法上,这些方法提供了一种新颖的算法来提高信用评分的准确性。这些方法包括统计方法,如线性判别分析(Linear Discriminant Analysis, LDA) [1] 和逻辑回归(Logistic Regression, LR) [2] ,以及人工智能方法,如人工神经网络(Artificial Neural Networks, ANN) [3] 支持向量机(Support Vector Machines, SVM) [4] 和决策树(Decision Tree, DT) [5] 。尽管基于人工智能的方法取得了突破,但LDA和LR等简单型仍然是流行的信用评分方法,因为它们易于实施且准确 [6] 。
国内在信用风险评估领域起步较晚,最初主要依赖专家经验进行评估,容易存在主观性误差。然而,自2003年起,机器学习方法开始引入信用风险评估。李萌 [7] (2005)利用主成分分析构建Logistic回归模型评估商业银行信用风险。郑昱 [8] (2009)通过Probit模型发现职业稳定性和过去信贷状况是影响个人信用的主要因素。支持向量机在1995年提出,适用于二分类问题,可以通过核方法进行非线性分类。姚潇和余乐安 [9] (2012)将支持向量机应用于信用风险评估,并证明其具有良好的判别效果。任潇等 [10] (2016)比较了四种常见的单一模型,发现SVM方法效果最好。随着算力提升和机器学习的发展,集成学习在个人信用风险评估中得到广泛应用。集成学习通过训练多个弱分类器并组合其结果来提高预测效果。集成学习包括Bagging和Boosting两种类型。随机森林是一种常用的Bagging集成算法,在商业银行和贷款机构应用广泛。方匡南、吴见彬等 [11] (2010)利用随机森林评估信用风险,并取得良好表现。Boosting是一种串行集成方法,代表算法有AdaBoost、XGBoost和LightGBM。白鹏飞 [12] (2017)研究发现XGBoost在互联网信贷风险评估中表现优于其他模型。LightGBM是微软团队在2017年提出的轻型GBDT梯度提升框架,具有较低的运算量和内存消耗。朱丽云 [13] (2020)构建了LightGBM模型,并应用于个人信用风险评估,取得了良好的效果。刘晓晨 [14] (2020)发现Boosting集成方法在个人信用评估中表现较好。
本文以阿里天池公开的贷款违约数据,包括用户基本信息,首先对数据进行一些统计性分析,然后对数据进行数据清洗,特征编码,特征衍生,特征选择等一些预处理,最终提取了20维的特征变量。构建了双阶段异构堆叠模型,并对模型进行贝叶斯调参优化,通过K折交叉验证的方式利用AUC值,准确率进行模型评估。本文主要研究了双阶段异构堆叠集成模型在金融信贷违约中的应用,已经有很多学者证明集成学习相比传统的模型预测的更加正确,但对于双阶段异构堆叠集成模型 [15] 在金融信贷违约风险预测的应用还很少。本文将多个较为前沿的集成方法应用到了金融信贷风险预测中并进行比较,分析得出了相比传统的模型预测,双阶段异构堆叠集成模型效果更好。
2. 集成学习的基础
任何集成学习系统的一般框架都是使用聚合函数G来组合一组基线分类器
用于预测单个输出。给定大小为n的数据集和维度的特征:
(1)
基于该集成方法的输出预测由式(1)所示:
(2)
图1说明了集成学习的一般抽象框架。所有集成都由一组基线分类器(分类器集成)组成,这些分类器已在输入数据上进行训练,这些输入数据产生预测,这些预测组合在一起以产生聚合预测。
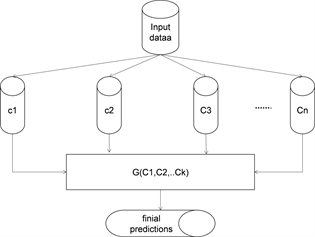
Figure 1. General framework of Ensemble
图1. Ensemble的一般框架
2.1. 基础分类器
2.1.1. 支持向量机
SVM的基础是由Vapnik开发的,由于其各种吸引人的特性和有前途的性能而获得认可。该公式体现了结构风险最小化原则,并优于传统机器学习方法所采用的传统经验风险最小化原则。
SVM主要描述使用支持向量方法进行分类。在分类问题中,目标是通过从可用示例中诱导的函数来分隔两个类,并且分类器在看不见的示例上工作得很好,即它能很好地泛化。2中的一个简单的例子阐明了这一概念。请注意,许多可能的线性分类器可以分离数据,但只有一个分类器可以最大化边距。这种线性分类器被称为最佳分离超平面(图2)。
2.1.2. KNN
K最近邻(KNN)算法是一种基本的分类和回归方法。该算法的核心思想是通过测量不同特征值之间的距离来进行分类。在分类问题中,KNN算法会寻找与新样本数据最接近的训练样本,然后根据这些邻居的类别进行投票来确定新样本的类别。在回归问题中,KNN算法会采用邻居样本的平均值来对新样本进行预测。KNN算法的关键参数是K值的选择。K值的选择会直接影响模型的性能,较小的K值会使模型更加复杂、容易受到噪声干扰,而较大的K值会使决策边界更加平滑,但可能忽略了样本局部特征。KNN算法简单易用,无需估计参数,适用于多分类问题。该算法的缺点是计算成本高,在数据量大时性能较差;对异常值敏感;需要事先确定K值。针对KNN算法的缺点,研究者们提出了很多改进版本,如加权KNN、基于树结构的KNN (如KD树、Ball树)等。KNN算法在实际中被广泛应用于模式识别、图像处理、推荐系统等领域。
2.1.3. 朴素贝叶斯
朴素贝叶斯算法是一种基于概率统计的分类算法,它基于贝叶斯定理和特征条件独立假设。该算法常被用于文本分类、垃圾邮件过滤、情感分析等领域。朴素贝叶斯算法的核心思想是通过计算给定类别下特征的条件概率来进行分类。它假设每个特征与其他特征之间相互独立,这也是“朴素”一词的来源。具体而言,对于一个待分类的样本,朴素贝叶斯算法会计算其在每个类别下的后验概率,并选择具有最高后验概率的类别作为最终的分类结果。朴素贝叶斯算法的关键是学习每个类别下特征的概率分布。通常采用极大似然估计或平滑技术来估计这些概率。常见的朴素贝叶斯算法包括多项式朴素贝叶斯、伯努利朴素贝叶斯和高斯朴素贝叶斯等。朴素贝叶斯算法具有以下优点:简单高效,易于实现和理解;对小规模数据表现良好;适用于多分类问题。然而,朴素贝叶斯算法的缺点是对特征之间的依赖关系做了较强的假设,可能导致分类性能下降。综上所述,朴素贝叶斯算法是一种基于概率统计的分类算法,具有简单高效、易于实现等优点,在文本分类、垃圾邮件过滤等领域有广泛应用。
2.2. 元学习器
RF (Random Forest, RF)分类器是一种集成分类器,它使用一组CART (Classification and Regression Tree)进行预测 [16] 。树是通过替换(装袋方法)绘制训练样本的子集来创建的。这意味着可以多次选择相同的样品,而其他样品可能根本无法选择,如图3所示。
随机森林分类器的训练和分类阶段:i = 样本,j = 变量,p = 概率,c = 类,s = 数据,t = 树数,d = 要分类的新数据,value = 变量,j可以具有的不同值。大约三分之二的样品(称为袋内样品)用于训练树木和剩余的三分之一(称为袋外样品)用于内部交叉验证技术,以估计所得RF模型的性能。
此误差估计称为袋外(OOB)误差。每个决策树都是独立生成的,无需任何修剪,每个节点都使用用户定义的特征数量(Mtry)进行拆分,这些特征是随机选择的。通过将森林增加到用户定义的树数(Ntree),该算法创建了具有高方差和低偏差的树。最终的分类决策是通过平均(使用算术平均值)所有生成的树计算的类分配概率来做出的。因此,根据集成中创建的所有决策树评估新的未标记数据输入,并且每个树都投票选出一个类成员。得票最多的会员等级将是最终选择的等级(图4)。
3. 双阶段异构集成模型
集成方法通过训练多个分类或者回归算法以获得比任何基本算法具有更高精度的结果模型。它使用不同的技术来实现,如投票、堆叠和混合等。叠加是本文实现的一种集成算法。它的工作原理是将选定的基本算法分为两层,其中第一层形成模型堆栈,第二层是原学习分类器。堆叠组合了三个或者更多不同模型的优点,以产生高度的准确性和控制过拟合。当它与不同的基本算法混合使用时效果最好,这些基本算法独立产生非常不同的结果。图5为堆叠集成算法的2个阶段;训练数据首先被反馈送到模型堆栈,然后将预测结果输入到第二阶段(元学习器)得到结果,元学习器与基础学习器的预测相匹配,从而做出更准确的预测。下列是建议模型的步骤。
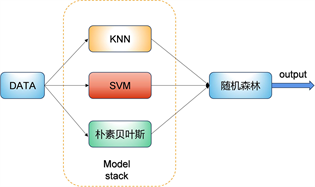
Figure 5. Stacked integrated learning algorithm
图5. 堆叠集成学习算法
第一步是确定N个基本算法,这些算法构成堆栈模型(以及模型的参数),并最适合训练数据集。接下来我们选择一个元学习算法,它构成了集成的第二阶段,在这一步中,我们在数据集上训练所选的N个基本算法,接下来将数据集分为K个部分,对每个分类算法进行交叉验证,并收集N个基本算法的预测结果,得到结果后,编译M*N矩阵,作为下一阶段的输入,这里M是N个基本算法的预测值,这些结果被称为第一阶段的结果。接下来我们在第一阶段分类器得到的结果上训练元学习算法,这些来自作为元学习器输入的基本模型的预测是“样本外”数据,这意味它们没有用于训练基本模型。元学习器的最好地结合了基础模型的预测,并对数据集的测试训练分割的不同比例得到结果。最后,我们在不同的测试数据上对集合进行测试,并评估预测精度。
4. 实验数据采集及预处理
4.1. 数据字段说明
在本研究中,使用天池比赛贷款数据集进行建模和测试,该数据集包括47列变量信息,如信用等级、贷款金额、最新支付信息、信用评分、财务查询数量和地址,其中15列为匿名变量。删除了一些没有建模价值的数据,包括当前贷款流程不完整和特征严重缺失的记录,删除率为3.7%。最后,保留200,000条比较完整的贷款记录作为初始数据集。数据集所包含的部分字段如表1所示。

Table 1. Partial field descriptions
表1. 部分字段描述
4.2. 分类变量与违约状态可视化
在明确数据的来源和变量含义后,进行数据探索是研究的第一步。我们首先查看了数据集中各变量的描述统计量,并对标签的分布进行了初步探索。数据集包含20万条记录,其中违约为0的记录有16,052条,占比80.5%;违约为1的记录有38,948条,占比19.5%。可以看出,正负样本的比例接近4:1,存在样本不平衡问题,这在金融风险评估中是常见的情况。大多数人并不会发生违约。
针对本文研究的二分类问题,通过可视化变量与标签之间的关系进行了初步探索。图6展示了标签的取值分布,数据共20万条记录,违约为0的有16,052条记录,违约为1的有38,948条记录,正负样本接近4:1,存在样本不平衡现象,这是金融风险评估的常见现象。图7为工作年限与违约的关系示意图,可以看出,工作年限超过10年的贷款记录最多,可能是因为工作年限越长,工作越稳定,可以稳定偿还贷款,违约的可能性比较小。此外,图7中可以看出各个工作年限的违约情况相差不大,一般情况下工作年限为1年的应该是应届毕业生,但是违约的占比和工作多年的违约占比差别不大,可能是因为个人消费贷款,金额小,所以还款没有压力。
图8为贷款等级占比,数据集中将贷款等级分为A~G七个等级。其中,贷款等级为B和C的数量最多,而贷款等级为G的数量最少。可能由于经过银行对借款人的综合考评,此类借款客户由于自身信用或其他原因导致其违约可能性很大,因此该等级的人能较难申请到银行贷款。图9为贷款等级与违约状态的关系示意图,可以看出,贷款等级为F和G的违约可能性最大,已经超过了40%;而贷款等级为A的违约可能性最低,仅占5%。随着贷款等级的提高,违约风险逐渐降低。因此,我们可以假设贷款等级对违约有一定的影响。

Figure 7. Percentage of work-years in default
图7. 工作年限违约占比
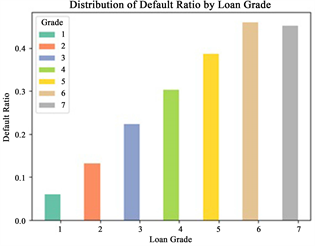
Figure 9. Percentage of loan-grade defaults
图9. 贷款等级违约占比
4.3. 连续变量与违约状态可视化
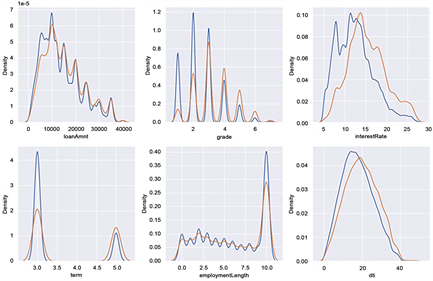
Figure 10. Partial characteristic kernel density curves
图10. 部分特征核密度曲线
图10是部分特征的核密度曲线,在违约和不违约的条件下KDE核密度曲线存在差异,说明其在违约预测中起到一定的作用,可以初步假设它对贷款违约预测有影响。像interestRate中在违约和不违约状态下的分布有明显差异,利率越高的违约用户最多。而对于核密度曲线几乎完全重合的特征,可以假设它对贷款违约预测没有影响。
图11表示了数据集部分特征分布可视化图,这些直方图是使用python中的数据可视化库绘制的,可以看出这些特征分布较为均匀,不存在特别不平衡的情况。从图中可以看出贷款金额多数集中在10,000~20,000之间,最高贷款4万左右,可知样本的贷款金额范围不大。贷款年限大多数都分布在10年及以上。

Figure 11. Visualisation of the distribution of some features
图11. 部分特征分布可视化
4.4. 数据清洗
在对实际的研究问题中,我们挖到的数据往往会出现数据缺失,数据不平衡等问题,在进行模型训练之前需要对数据进行处理,处理结果会影响模型的建立和数据分析的质量。在本研究中,id是唯一标识的,对实验没有帮助,将它删除,并且grade和subgrade是完全相同的特征,这里将subgrade特征删除。
4.4.1. 文本处理
步骤一:对贷款等级grade进行特征编码,将A~F改为1~6;
步骤二:对贷款发放日期issuedata转化为时间格式;
步骤三:将贷款年限employmentLength中的缺失值用中位数补充,并将<1 year用0替换,最后将year关键词删除,得到相应的工作年限;
步骤四:求出各个特征与目标的相关系数,综合考虑排除相关性小于0.01的特征initialListStatus,n5,n11,n12,n8,postCode;
步骤五:将相关性过高installment,interestrate进行删除;
步骤六:对于高基数特征,为了更好地表示这种分类特征与目标变量之间的关系,使用一些特征编码技术来将其衍生出新的特征列grade_to_mean_n0,grade_to_mean_n1等,将数据特征扩展到80列。
4.4.2. 缺失值处理
数据集train共有47列,有22个特征含有缺失值,部分特征缺失比例如表2,可以看出存在缺失值的特征有employmentTitle、employmentLength、匿名变量n0、n1、n3、n11等等,其中n11的缺失比例最大,employmentTitle的缺失比例最小,对匿名变量n0、n1、n3、n11的分析可知n0、n1、n3缺失的数量一样,有可能缺失的都是相同的行,经代码验证得,n0缺失的行,n1、n3、n11均缺失;n11缺失的行,n0、n1、n3部分缺失,说明n11缺失与n0、n1、n3缺失存在某种对应关系,虽然n0、n1、n3、n11字段含义并不清楚,但观察它们取值可以发现,取值均为整数,且均呈右偏分布,考虑用中位数来填充缺失值;同样employmentTitle取值也为整数,且呈右偏分布,因此对employmentTitle也使用中位数来补齐。对于employmentLength这样的特征,因为数据集存在与之相关的特征,所以对employmentLength用决策树填补就业年限,对于分类变量采用众数填补缺失值,对于连续变量采用中位数填补缺失值。

Table 2. Proportion of partial features missing
表2. 部分特征缺失比例
4.4.3. 异常值处理
通过描述统计发现policyCode具有唯一值1,将其删除。为检测是否存在其他异常值,绘制箱线图如图12所示,对于其他存在异常值的变量,不作处理,这是因为在金融风控领域中,异常值的存在是有意义的,可能会包含其他有用的信息,有时常被看成是一种风险,所以不可轻易处理。
4.5. 特征工程
在数据清洗之后,便可以进行特征构建了。特征构建也可以称为特征衍生,是根据数据集的现有特征结合业务理解去衍生出新的具有意义的特征,由于我们所得到的数据维度较小,且都是简单的单一特征,不包含由公式计算得到的复杂特征,其含有的有用信息较少,需要通过寻找特征之间的关系构建衍生特征来体现,通常是已有数据的组合。通过对数据集中特征的观察并结合前期的分析,有以下几点思考。第一,可以根据贷款发放时间issueDate和信用额度开立时间earliesCreditLine相减来构造特征Issue_Earlies_Diff:审批发放时长 = 贷款发放时间 − 信用额度开立的时间 = issueDate − earliesCreditLine;
第二,贷款评分与是否违约之间具有一定的关联,可以根据上下限分数加权平均构造特征fico_average,并将评分上限和下限删掉;fico所属平均范围=(借款人在贷款发放时的fico所属的下限范围 + 借款人在贷款发放时的fico所属的上限范围)/2 = (ficoRangeLow + ficoRangeHigh)/2;
第三,从数据缺失情况来看,由于n0、n1、n3、n11的缺失之间似乎存在某种关联,尝试以n0和n11为例构建特征n0_n11:取值为0时表示n0和n1均不缺失,取值为1表示n0和n11均缺失,取值为2表示n0缺失,n11不缺失;
第四,贷款结束的年份可能会受外部环境或市场变化的影响而间接影响还款意愿,因此考虑通过贷款发放时间issueDate和贷款年限term相加来构造特征end_year:贷款结束的时间 = 贷款发放时间 + 贷款年 = issueDate + term。
4.5.1. 特征选择
在原有特征的基础上构建完衍生特征后,需要对所有的特征进行筛选,选择对违约预测有用的特征加入到模型中。并不是所有的特征都能提高模型的精度,特征筛选是机器学习中的一个关键步骤,它可以帮助我们选择具有重要预测性能的变量,并在模型训练中减少噪音和复杂性。常见的特征筛选方法包括相关系数法、模型自身特征筛选和IV值筛选。相关系数法是一种基于Pearson相关系数计算变量之间线性相关性的方法,如果相关系数高于给定的阈值,则删除其中一个变量。这种方法适用于处理高度相关的变量,但并不适用于非线性关系的变量。模型自身特征筛选是指在建立机器学习模型的过程中,同时进行特征选择和模型训练。这种方法可以根据评价指标自动筛选变量,从而提高模型的准确性和效果。集成学习模型如随机森林和LightGBM就是利用这种方法进行特征选择。这种方法在处理非线性关系的变量时表现良好。IV值筛选特征是一种基于变量的预测能力进行量化的方法。IV值越大,代表变量的预测能力越高。IV值的计算是以WOE分箱为基础的。逻辑回归常用IV值进行特征筛选,其他机器学习方法则采用机器学习本身的自动筛选特征功能。本实验采用的是相关性系数法,选用特征重要性最高的20个特征进行训练,这样既可以降低模型的复杂度也可以减少训练时间,图13是特征重要性图,特征重要性图可以帮助我们识别哪些特征对于预测结果最为重要,这有助于我们选取最优的特征来进行建模,减少模型训练的时间和计算成本。我们将数据分为两组:训练集、和测试集,权重分别为80%、20%。
4.5.2. 平衡数据集
观察数据集中的isDefault标签的数量分布显示,其中取值为0的样本数占总体样本的19.5%,而取值为1的样本数占总体样本的80.5%,呈现出明显的不平衡状态。考虑到正样本数量较少,欠采样会导致整体数据量减少,不利于模型的训练和泛化能力。因此,针对不平衡数据集,我们选择使用过采样方法来平衡数据分布。具体而言,我们尝试了随机过采样、SMOTE过采样以及SMOTE与Tomek Link结合使用的综合采样三种方法。通过比较这三种方法在评估指标上的表现,我们可以选择最适合的方法来处理不平衡数据。在进行过采样时,我们需要保留部分原始数据用于评估采样效果。因此,我们首先将数据集按照8:2的比例划分成训练集和测试集,然后分别采用以上三种过采样方式增加正样本数量。接着,将三种方法得到的样本分别放入随机森林、SVM和朴素贝叶斯模型中进行拟合,并利用之前划分出来的测试集来评估三种方法在三个模型上的表现。经过验证后发现,对于该数据集,随机过采样后的数据在三个模型上的测试集AUC值均高于SMOTE采样和综合采样。具体而言,在随机森林模型上,测试集AUC值为0.837877;在SVM模型上,测试集AUC值为0.817957;而在朴素贝叶斯模型上,测试集
AUC为0.805264。综上所述,根据实验结果,我们选择随机过采样方法来平衡数据集,以提高模型性能和预测准确度。随机过采样方法能够在处理不平衡数据时取得良好的效果,有助于提升模型的泛化能力和预测性能。
图14描述了DH-SEM的完整流程图,其中包括对预处理数据集、集成训练和预测分类。
步骤1:该数据集由多个特征组成,经数据处理和最由特征选择。
步骤2:数据被划分为80:20的训练测试比。
步骤3:然后由三个基础学习器和1个元学习器组成的堆叠集成对这些数据进行训练和测试。
步骤4:预测结果将数据分为两类,即违约和不违约。
集成模型的时间复杂度计算为SVM、KNN和朴素贝叶斯的最大时间复杂度与随机森林元学习器的时间复杂度之和。
4.6. 模型参数设置
首先,用随机过采样平衡后的数据集作为训练集,使用默认参数构建随机森林模型,用前期划分的未参与采样处理的原始数据作为测试集,用于评估随机森林的模型效果。其次,通过网格搜索来对随机森林的超参数进行调整。调整得到的最优超参数如表3所示。KNN和SVM的模型参数如表4,表5所示。

Table 3. Random forest parameter settings
表3. 随机森林参数设置
4.7. 评价方法
为了评估我们的模型,我们使用了四个最常用的评估指标,即准确率、精确率、召回率和F1分数(宏),这是用于评估文本分类的典型方法。
它们的计算方法如下:
(3)
(4)
(5)
(6)
TP (真阳性)表示将阳性样本预测为阳性,TN (真阴性)表示将阴性样本预测为阴性,FP (假阳性)表示将阴性样本预测为阳性,FN (假阴性)表示将阳性样本预测为阴性。
5. 实验结果与讨论
本节讨论了金融信贷违约问题的建议技术的结果,以及其性能的评价与原有研究的比较。首先,将数据集分为80%的训练数据点和20%的测试数据点,并将类标记为违约为1,不违约为0。用于训练模型的计算系统有一个2.4 GHz的英特尔四核i5处理器和12 gb的随机存取存储器。Python语言用于编写Jupyter笔记本中的算法脚本。
采用支持向量机、KNN、朴素贝叶斯作为基础学习器,随机森林作为元学习器,建立堆栈集成模型。选择SVM作为集成堆栈中的一种算法,因为它在小数据集和两类明显分离的情况下表现良好。使用KNN是因为它随着新的数据点不断进化,只有一个超参数需要调整,并且训练时间复杂度最小。朴素贝叶斯是一个理想的选择作为分类器,由于其快速的实时预测和高准确性。该算法中使用的随机森林元学习器对基础学习器的预测进行拟合,并试图克服基础学习器的局限性。在对数据集进行堆叠集成模型训练之前,先对堆叠中使用的每个模型和元学习器的测试精度进行了测量。这些结果以及堆叠集成学习算法的测试成绩如表6所示。该表的结果显示,与随机森林元学习器相比,前三个基本模型的性能相对较差。但是,堆叠集成能够最好地将这些结果结合起来,形成一个高度精确的模型,这是它与其他机器学习技术的区别。

Table 6. Comparison of stacked models with individual algorithms
表6. 堆叠模型与单个算法的比较
ROC曲线
绘制了ROC曲线来评估算法的工作效果。ROC曲线下的面积显示了分类器区分类别之间差异的程度。AUC越高,表明模型在区分正类和负类。如果一个模型显示出100%的准确性,那么它的AUC为1,而无法正确预测任何类别的模型的AUC为0。图15显示了考虑模型的ROC曲线。
6. 结论
这项工作探索了基于阿里天池数据集的个人信息特征来确定是否违约的集成学习。研究了DH-SEM技术在金融信贷违约的分类性能。随机森林元学习器提高了预测精度,控制了过度拟合。利用ROC曲线对该方法进行了性能评价。与现有方法相比,该集成模型的性别识别准确率达到88.6%。