摘要: 本文运用 Leggett-Williams 不动点定理讨论了具有平均曲率算子 Robin 边值问题
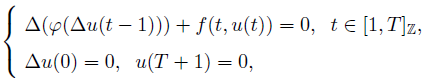
三个正解的存在性, 其中, Z 表示整数集,[1, T ]Z := {1, 2, ..., T − 1, T}, T ≥ 2 是正整数,
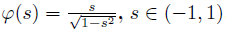
, s ∈ (−1, 1),非线性项 f : [1, T ]Z × [0, ∞) → [0, ∞) 连续,∆ 是前项差分算子。
Abstract:
In this paper, by using the Leggett-Williams fixed point theorem, we give the existence of three positive solutions for the following Robin boundary value problem with mean curvature operator
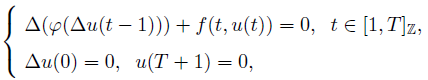
where Z denotes the integer set, [1, T ]Z := {1, 2, ..., T − 1, T}, T ≥ 2 is an integer,
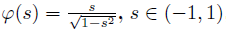
, Nonlinear term f : [1, T ]Z × [0, ∞) → [0, ∞) is operator continuous, ∆ is the forward difference operator.