分数阶Kirchhoff-SchrÖdinger-Poisson系统解的存在性
Existence of Nontrivial Solution for a Class of Fractional Kirchhoff-SchrÖdinger-Poisson System
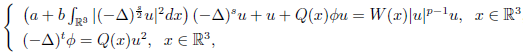
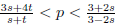
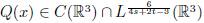
摘要: 本文研究如下分数阶Kirchhoff-SchrÖdinger-Poisson系统, 非平凡解的存在性, 其中 a, b > 0 ,,  s, t ∈ (0, 1) 且 4s + 2t > 3, W (x) ∈ C(R3) 变号且 lim|x|→∞ W (x) = W∞ < 0 , . 应用山路引理, 本文得到该系统至少存在一个非平凡解.
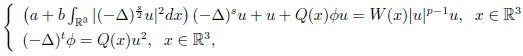
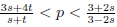
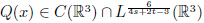
Abstract: In this paper, we study the existence of nontrivial solution for fractional Kirchhoff- SchrÖdinger-Poisson system:, where a, b > 0, , s, t ∈ (0, 1) and 4s + 2t > 3, W (x) ∈ C(R3) is a sign-changing function with lim|x|→∞  W (x) = W∞ < 0, . By using mountain pass lemma, we obtain that this system has at least one nontrivial solution.
文章引用：张召翔. 分数阶Kirchhoff-SchrÖdinger-Poisson系统解的存在性[J]. 应用数学进展, 2024, 13(5): 2191-2198. https://doi.org/10.12677/AAM.2024.135208

参考文献

[1] Deng, Y.B., Peng, S.J. and Shuai, W. (2015) Existence and Asymptotic Behavior of Nodal Solutions for the Kirchhoff-Type Problems in R3. Journal of Functional Analysis, 269, 3500- 3527. [Google Scholar] [CrossRef] 
[2] He, Y. (2016) Concentrating Bounded States for a Class of Singularly Perturbed Kirchhoff Type Equations with a General Nonlinearity. Journal of Differential Equations, 261, 6178- 6220. [Google Scholar] [CrossRef] 
[3] Li, G. and Ye, H. (2014) Existence of Positive Ground State Solutions for the Nonlinear Kirchhoff Type Equations in R3. Journal of Differential Equations, 257, 566-600. [Google Scholar] [CrossRef] 
[4] Mao, A. and Chang, H. (2016) Kirchhoff Type Problems in RN with Radial Potentials and Locally Lipschitz Functional. Applied Mathematics Letters, 62, 49-54. [Google Scholar] [CrossRef] 
[5] Wang, D.B. (2020) Least Energy Sign-Changing Solutions of Kirchhoff-Type Equation with Critical Growth. Journal of Mathematical Physics, 61, Article 011501. [Google Scholar] [CrossRef] 
[6] Xie, Q., Ma, S., Zhang, X. (2016) Bound State Solutions of Kirchhoff Type Problems with Critical Exponent. Journal of Differential Equations, 261, 890-924. [Google Scholar] [CrossRef] 
[7] 陈莉萍. 一类带变号权Kirchhoff方程解的存在性[J]. 应用数学进展, 2023, 12(4): 1567-1573. [Google Scholar] [CrossRef] 
[8] Willem, M. (1996) Minimax Theorems. Birkha¨user, Boston. [Google Scholar] [CrossRef] 
[9] Cerami, G. and Vaira, G. (2010) Positive Solutions for Some Non-Autonomous Schro¨dinger- Poisson Systems. Journal of Differential Equations, 248, 521-543. [Google Scholar] [CrossRef] 
[10] Yu, X.H. (2011) Existence of Solutions for Schro¨dinger-Poisson Systems with Sign-Changing Weight. Journal of Partial Differential Equations, 24, 180-194. [Google Scholar] [CrossRef] 
[11] 余晓辉. 一类薛定号-泊松方程解的存在性[J]. 应用数学, 2010, 23(3): 648-652.
[12] 孟娟霞. 一类分数阶薛定号-泊松系统非平凡解的存在性[J]. 应用数学进展, 2023, 12(4): 1704-1712. [Google Scholar] [CrossRef] 
[13] Laskin, N. (2000) Fractional Quantum Mechanics and L´evy Path Integrals. Physics Letters A, 268, 298-305. [Google Scholar] [CrossRef] 
[14] Laskin, N. (2002) Fractional Schro¨dinger Equation. Physical Review E, 66, 56-108. [Google Scholar] [CrossRef] 
[15] Bisci, G.M., R˘adulescu, V.D. and Servadei, R. (2016) Variational Methods for Nonlocal Frac- tional Problems. Cambridge University Press, Cambridge.

为你推荐