LFP(ε)上两种拓扑的比较与LFP(S)的完备性
A Comparison of Two Topologies for LFP(ε) and the Completeness of LFP(S)
DOI: 10.12677/PM.2013.31013, PDF, HTML,   
作者: 吴明智*：北京航空航天大学数学与系统科学学院；赵 媛*：河北金融学院基础部
关键词: 随机赋范模； (ε；λ)-拓扑；依概率收敛拓扑；Random Normed Module; (ε；λ)-Topology; Topology of Convergence in Probability
摘要: 首先，本文对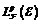上的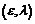-拓扑和依概率收敛拓扑作了一点初步的对比。接着，以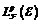为桥梁，利用其上两种拓扑的关系，运用随机赋范模理论中的一些结果给出Stricker引理的证明。最后，本文证明随机赋范模S生成的随机赋范模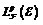是完备的当且仅当S是完备的。
Abstract: First, we make a primary comparison of the -topology and the topology of convergence in probability for 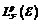. Then, using the relation of the two kinds of topologies for 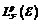, we give a proof of Stricker’s lemma based on a result in the theory of random normed modules. At last, we show that the random normed module 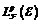is complete if and only if is complete.
文章引用：吴明智, 赵媛. LFP(ε) 上两种拓扑的比较与LFP(S) 的完备性[J]. 理论数学, 2013, 3(1): 81-86. http://dx.doi.org/10.12677/PM.2013.31013

参考文献

[1] D. Filipović, M. Kupper and N. Vogelpoth. Separation and duality in locally -convex modules. Journal of Functional Analysis, 2009, 256: 3996-4029.
[2] D. Filipović, M. Kupper and N. Vogelpoth. Approaches to conditional risks. Working Paper Series No. 28, Vienna: Vienna Institute of Finance, 2009.
[3] T. X. Guo. Recent progress in random metric theory and its applications to conditional risk measures. Science China Mathematics, 2011, 54(4): 633-660.
[4] T. X. Guo. Relations between some basic results derived from two kinds of topologies for a random locally convex module. Journal of Functional Analysis, 2010, 258: 3024-3047.
[5] T. X. Guo, S. B. Li. The James theorem in complete random normed modules. Journal of Mathematical Analysis and Applications, 2005, 308: 257-265.
[6] M. Z. Wu. The Bishop-Phelps theorem in complete random normed modules endowed with the -topology. Journal of Mathematical Analysis and Applications, 2012, 391: 648-652.
[7] 严加安. 测度论讲义[M]. 北京: 科学出版社, 2004.
[8] B. Schweizer, A. Sklar. Probabilistic metric spaces. New York: Dover Publications, 2005.
[9] H. Fӧllmer, A. Schied. Stochastic finance, an introduction in discrete time. Berlin, New York: Walter de Gruyter, 2002.
[10] T. X. Guo, G. Shi. The algebraic structure of finitely generated -modules and the Helly theorem in random normed modules. Journal of Mathematical Analysis and Applications, 2011, 381: 833-842.

为你推荐