1. 引言
1.1. 研究背景与意义
我国目前正处在经济社会发展转型和人口结构变化的关键时期。错综复杂的社会局面,让我们正处在向劳动力供求关系发展转变的十字路口。一方面,在“人口红利”和市场经济的快速发展后,低出生率问题在中国老龄化过程中进一步加剧,并且很快地就进入了中国劳动年龄人口负增长的历史转折点。另一方面,进入21世纪以来,国家调整经济转型和产业结构,这一措施扩大了第三产业发展和劳动力需求关系的发展路径,但经济的快速增长并没有带来强劲的劳动力需求。
我国经济稳定发展的关键是劳动力供求平衡,同时人口结构变动也是最重要的因素,它会引发各种社会问题。当前我国人口结构变化的特点:1) 劳动年龄人口总量呈下降趋势;2) 老龄化和少子化;3) 抚养比进入上升通道;4) 劳动力素质提高显著;5) 加速城镇化政策出台对人口城乡结构变化影响显著 [1] 。就业是民生之本,研究人口结构转变对就业形势的影响无论对国家,对人民都具有深刻的意义。本文将人口结构分为三个子结构:自然、社会经济、地域结构,对子结构与就业之间的关系进行研究分析。目的在于准确把握人口发展形势和就业人口相互作用的客观规律,从而促进人口、经济和社会的持续健康发展。
1.2. 研究现状
近年来人口结构发生变化,人力资源需求的变化和新技术革命使得就业形式日益严峻,从人口结构来研究其对就业形式的影响,国内外学者从人口出发针对就业形式问题展开了深入的研究。朱文涛等基于全国1978~2013年时序数据构建了VAR模型,并探究人口城镇化、就业非农化与城乡收入差距之间的关系,结果显示:前两者与城乡收入差距存在一种长期均衡的关系 [2] 。莫旋等根据我国流动人口的动态监测数据建立了分层多元选择模型,以分层和异质性的视角,深入研究了影响流动人员就业率的各种因素以及流动人员的职业选择,研究成果表明:流动人员在不同职业身份的情形下具有的要素禀赋具有显著差异,以及不同的要素禀赋将会对其职业选择产生深远影响,创业型就业更受老一代欢迎,而务工型就业更受年轻一代欢迎 [3] 。林耿等对广东省的21个地级市进行就业空间研究,对两类人口的就业构成、类型区进行研究,结果表明:体制内就业更受常住人口喜欢,常住人口有也比流动人口有更多元化的就业空间分异,但是两者就业空间并没有造成社会两极分化 [4] 。
针对人口与就业的时间序列数据,多采用向量自回归(VAR)模型、长短期记忆网络(LSTM)模型等进行分析与预测。刘宏等基于全国1985~2010年外国直接投资、经济增长以及就业这三个时序数据构建VAR模型。研究表明:外国直接投资对我国经济增长和就业产生了加速效应 [5] 。Yang等针对多元时间序列数据,对VAR模型进行了改进,提出了一种新的VARMA在线时间序列预测框架,证明了VAR可以在在线设置下模拟基础VARMA模型,在这个框架下,开发了两种有效的算法VARMA-OGD和VARMA-ONS来解决时间序列预测问题 [6] 。Li等采用聚类分析法对毕业生就业形式进行研究,预测了毕业生就业情况,提出了一种基于长短时记忆(LSTM)递归神经网络的毕业生就业状况预测技术(网络结构设计、网络训练等),验证了LSTM及其参数优化算法在毕业生就业形势分析中的适用性和正确性 [7] 。
2. 模型介绍
2.1. 向量自回归模型
一般的VAR (p)模型的数学表达式是:
(1)
其中
是
阶时间序列列向量。c是
阶常数项列向量。
到
表示
阶参数矩阵。
表示
阶外生变量向量。
到
是
阶待估系数矩阵。
是
随机误差列向量。
2.2. 长短期记忆模型
长短期记忆网络(LSTM)是一种循环神经网络(RNN)的变体,这种网络结构最初是由Hochreiter等人引入的,逐渐被完善为处理时间序列预测问题的工具。LSTM不同于RNN网络的内部结构,RNN存在长期依赖性,而LSTM的网络内部结构更为复杂,其通过输入门、遗忘门、输出门引入sigmoid函数并结合tanh函数,重复的模块不只是有一个简单的tanh结构,从而避免了RNN长期依赖性。LSTM通过门的结构来调控任何时间的状态,添加求和操作,将短期记忆和长期记忆相连接从而解决梯度消失的问题,LSTM具备删除或添加节点的能力,通过三个门的信息传递给单元状态,其中遗忘门决定以前的单元格信息是否传递到当前单元格,输入门从当前的输入中确定单元格的信息更新,当前单元格的输出基于最新状态、前一时刻输出和当前输入得到,也称作输出门,每一个门都由神经网络表示,都具备输入层、隐藏层和输出层。
LSTM在t时刻有3个输入值,分别是目前网络的输入、上一时刻网络的输出
以及上一时刻的单元状态
;同时,LSTM网络的2个输出值,分别是当前时刻输出结果
和现在的单元状态
。状态单元里面的信息由输入门控制留下或者删除,输出门则负责把状态单元的长期状态信息控制作为目前网络的输出。下列公式表示了长短期记忆网络在t时刻的各个状态单元的更新。
(2)
其中
表示sigmoid函数,
是t时刻的输入,
为遗忘门,
为输入门,
为输出门,W表示权重,b表示偏置。
3. 数据来源及指标选取
本文采用中国1998~2020年的时序数据,通过运用R、Eviews、Python软件来探究中国人口结构与就业形势之间的关系,数据来源于RESSET数据库、《统计年鉴》。在研究过程中,选取不同的人口子结构与就业之间进行分析,人口自然结构选取人口性别比、人口抚养比;人口社会经济结构选取家庭规模、城镇居民人均可支配收入、教育结构;人口地域结构选取反映城镇化水平的非农人口占比。对于就业形势,选取就业人口(表1)。
4. 实证分析
4.1. 数据预处理
对各个指标作方差齐性变换,变换之后的序列分别记为lnFM、lnPDR、lnFS、lnPDI、lnES、lnNAR、lnLP (图1)。

Figure 1.Time series diagram of population structure and employment population series
图1. 人口结构和就业人口序列的时序图
4.2. 平稳性检验
传统的建立VAR模型要求平稳的时间序列。但大多数序列是非平稳的,如果不处理直接运用可能会出现“伪回归”现象,所以要对非平稳序列进行差分处理成平稳序列再运用VAR模型。本文将对各个序列进行ADF检验来确定是否平稳,结果如表2。
由表2的结果知,在0.05显著水平下,对数序列lnFM、lnPDR、lnFS、lnPDI、lnES、lnLP这6个序列为非平稳;只有lnNAR这1个序列为平稳。对数一阶差分序列dlnFM、dlnPDR、dlnFS、dlnPDI、dlnES、dlnNAR、dlnLP这7个为平稳的序列。
4.3. 协整检验
本文通过ADF检验发现人口地域结构的lnNAR为平稳序列,因此对该变量不做协整检验;而对数序列lnFM、lnPDR、lnFS、lnPDI、lnES、lnLP都是非平稳的时间序列,而对数一阶差分之后的序列均为平稳序列,可以进行协整检验。本文将分别对人口结构的两个子结构(人口自然结构、人口社会经济结构)所选变量与就业人口之间进行协整检验。
由表3可知,在0.05的显著性水平下,−2.3355 < −1.95,因此人口自然结构与就业人口的残差序列1平稳,即存在协整关系;−0.1008 > −1.95,所以人口社会经济结构与就业人口的残差序列2非平稳,即不存在协整关系。

Table 3. ADF test results of two residual sequences
表3. 两个残差序列的ADF检验结果
4.4. 实证分析
4.4.1. 格兰杰因果检验
协整检验表明了就业人口与人口自然结构之间存在长期稳定的关系;而与人口社会经济结构没有这种关系,所以将LNFM、LNPDR、LNLP进行滞后一期和二期的Granger检验。但由表2的ADF平稳性检验可知,人口社会经济结构和人口地域结构的五个对数一阶差分序列都是平稳的,因此将DLNFS、DLNPDI、DLNES、DLNNAR、DLNLP进行滞后一期和二期的Granger检验。具体检验结果如下(表4)。

Table 4. Results of Granger test
表4. Granger检验结果
在人口自然结构中,由于人口性别比(lnFM)、人口抚养比(lnPDR)与就业人口(lnLP)之间存在相关性,因此将人口性别比(lnFM)、和人口抚养比(lnPDR)纳入VAR模型中的解释变量,就业人口(lnLP)为被解释变量;在人口社会经济结构中,由于家庭规模(dlnFS)与就业人口(dlnLP)不存在相关性,实际纳入VAR模型的变量为城镇居民人均可支配收入(dlnPDI)、教育结构(dlnES),就业人口(dlnLP);在人口地域结构中,非农业人口比重(dlnNAR)没有通过Granger因果检验,因此不采用人口地域结构指标建立VAR模型。
4.4.2. VAR模型构造及稳定性检验
①人口自然结构VAR模型
对数序列lnFM、lnPDR与lnLP存在协整关系,接下来对人口自然结构基于序列协整建立VAR模型。
根据表5结果可知,最优滞后期为2,则建立VAR (2)模型如下。

Table 5. Optimal lag period selection for model 1
表5. 模型1的最优滞后期选择
如图2所示,向量自回归模型对应的特征根的模长都小于1,说明构建的VAR模型具有稳定性。
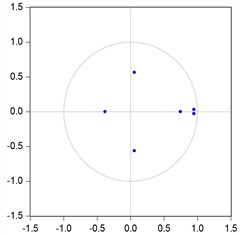
Figure 2. AR root graph of VAR (2) model
图2. VAR (2)模型AR根图
②人口社会经济结构VAR模型
对数一阶差分序列dlnPDI、dlnES、dlnLP为平稳序列,接下来对人口社会经济结构和就业人口基于平稳序列建立VAR模型。
根据表6结果可知,最优滞后期为1,则建立的VAR (1)模型如下。

Table 6. Optimal lag period selection for model 2
表6. 模型2的最优滞后期选择
如图3所示,向量自回归模型对应的特征根的模长都小于1,说明构建的VAR模型具有稳定性。

Figure 3. AR root graph of VAR (1) model
图3. VAR (1)模型AR根图
4.4.3. 脉冲响应函数分析
①人口性别比(LNFM)冲击就业人口(LNLP)
图4显示,人口性别比的正向冲击持续正向拉升就业人口,而且这种拉升效应一直在增强。由此可见,对于全国而言,人口性别比的增加在短期和长期都能够促进就业人口的上升,也可以解释为男性就业率比女性就业率高。

Figure 4. The impulse response function diagram of the employment population generated by the shock to the sex ratio of the population
图4. 人口性别比冲击产生的就业人口脉冲响应函数图
②人口抚养比(LNPDR)冲击就业人口(LNLP)
图5显示,人口抚养比的正向冲击对就业人口脉冲响应函数的负向影响开始逐渐增强。由此可见,人口抚养比的增加在短期和长期都会导致就业人口数目的下降,也可以解释为由于人口老龄化会导致人口抚养比增加,进而使得就业人口数目减少。

Figure 5. The impulse response function diagram of the employment population generated by the dependency ratio shock
图5. 人口抚养比冲击产生的就业人口脉冲响应函数图
③人均可支配收入(DLNPDI)冲击就业人口(LNLP)
图6显示,人均可支配收入在第一期对于就业人口的冲击几乎没有影响,在第二期达到最大的负向影响,从第五期逐渐稳定且为负。由此可见,长期来看人均可支配收入对于就业人口具有负向作用,可以解释为人均可支配收入减少,就业人口就会增加。
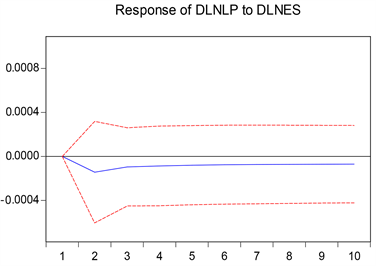
Figure 6. Impulse response function diagram of employment population generated by per capita disposable income shock
图6. 人均可支配收入冲击产生的就业人口脉冲响应函数图
④教育结构(DLNES)冲击就业人口(LNLP)
图7显示,教育结构施加的正向冲击持续正向拉升就业人口数目,而且这种拉升效应一直在增强,在第六期达到最大的正向影响,此后逐渐稳定并为正。教育结构反映的是接受高等教育及以上的情况。全国的教育结构近年来稳定缓慢上升,至2020年已经达到17.19%,也可以解释为受高等教育的人数越多,就业人口越多。
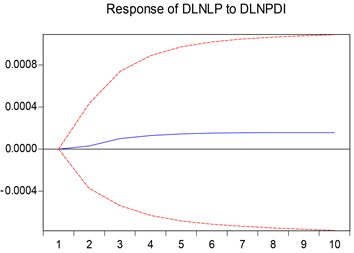
Figure 7. Impulse response function diagram of employment population caused by educational structure shock
图7. 教育结构冲击产生的就业人口脉冲响应函数图
4.4.4. 方差分解分析
方差分解进一步评价人口性别比、人口抚养比、人均可支配收入、教育结构的贡献度。
①人口自然结构方差分解结果
由表7可知,从短期来看人口性别比对就业人口数目影响不大,但在长期人口性别比波动对就业人口波动具有重要的影响,而且人口性别比对就业人口的波动要高于人口抚养比。

Table 7. The contribution rate of population sex ratio and dependency ratio to the employed population
表7. 人口性别比、抚养比对就业人口的贡献率
②人口社会经济结构方差分解结果
由表8可知,从短期来看人均可支配收入对就业人口数目影响较小,教育结构对就业人口影响较大;在长期人均可支配收入波动对就业人口波动有微小的影响,同样教育结构对就业人口的波动要高于人均可支配收入。

Table 8. The contribution rate of per capita income and educational structure to the employed population
表8. 人均可支配收入、教育结构对就业人口的贡献率
4.4.5. 拟合
①两个VAR模型的拟合
人口自然结构与人口社会经济结构的模型拟合优度分别为0.998953和0.950503,两个VAR模型拟合效果较好,图8和图9的拟合图也与之对应。

Figure 8. Fitting diagram of natural structure of population-VAR (2) model
图8. 人口自然结构-VAR (2)模型的拟合图
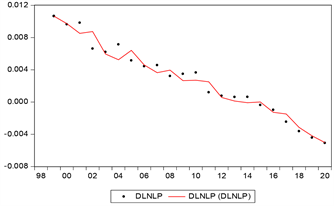
Figure 9. Population socioeconomic structure-fitting diagram of VAR (1) model
图9. 人口社会经济结构-VAR (1)模型的拟合图
②LSTM模型的拟合
对原始时间序列作归一化处理,训练集为前85%的数据,测试集为后15%的数据,输入层为人口结构的三个子结构出发所得6个因素,输出层为预测的1998年到2020年的就业人数,输入层的维度为6,输出层的维度为1,训练次数为3000,采用sigmoid函数作为激活函数。
运用三个指标对LSMT模型拟合结果进行评价:平均绝对误差、均方误差、均方根误差。平均绝对误差:
,能反映预测值误差实际情况,其值越小,模型的拟合效果就越好。均方误差:
,可以评价数据的变化程度,其值越小说明预测模型精确度更高。均方根误差
,用来衡量观测值和真实值的偏差 [8] (图10)。
运用Python软件计算得到模型评价指标值:MAE:0.12228;MSE:0.02218;RMSE:0.18214,说明该模型拟合效果很好。
5. 总结与建议
5.1. 总结
本文对人口结构的指标与就业之间的关系进行了实证分析,得出以下结论:格兰杰因果检验显示,人口性别比、人口抚养比、人均可支配收入、教育结构与就业人口之间具有相关性;脉冲响应函数分析显示,人口性别比、教育结构对就业人口具有长期的正向影响,人口抚养比、人均可支配收入对就业人口具有长期的负向影响;方差分解分析结果显示,人口自然结构中短期内人口抚养比对就业人口的影响大于人口性别比,但是长期来看人口性别比影响更大;人口社会经济结构中人均可支配收入对于就业人口的影响无论是长期还是短期均小于教育结构的影响;VAR模型与LSTM模型拟合效果都很好,但是VAR模型可解释性更强,是由于VAR通过其模型参数直接揭示了变量间的相互作用和联系,且每个系数都有明确的经济意义,可以直接解释为一个变量对另一个变量的影响强度和方向。
5.2. 建议
5.2.1. 建立健全养老保障体系
人口自然增长率下降,老年群体不断扩大,人口老龄化现象加重了年轻一代的压力,他们需要投入工作赚取更多的抚养资本,这使得相当一部分老年人口沦为“空巢老人”,而随着“空巢老人”数量的不断增加,家庭养老功能进一步弱化,养老难题成为社会有关部门的重点关注对象,社会负担加重,因此建立健全养老保障体系才会使社会经济稳定发展。
5.2.2. 大力发展教育事业
根据当前就业形势来看,毕业的人数逐年递增,竞争压力越来越大,要想在众人中脱颖而出,学历是首先考虑的一个因素。教育结构与就业人口关系较为紧密,其原因是用人单位更愿意招收高等院校毕业的学生,从而对就业人口稳定健康发展具有重要意义。每个城市的经济发展水平不同,部分城市在教育上的投入远低于发达城市。建议在未来政府应该加大对教育的投入、改善办学软件条件和硬件设施,以提高居民的文化水平、文化素质和劳动技能,让更多的人获取学历,营造良好的就业形势。