1. 前言
星系的光度距离和光度图,具体是logL-logdL图,简称dZL图。红移和光度图,为Z-logL图,简称为ZL图。光度在Z > 0.0041全电磁波段都适用。dZL图在所有文献中不存在。ZL图文献中虽有,但不是全部红移的图,或Z < 1,或红移某段局域图,已在文献 [1] 介绍上述2种图主要内容。下面由新引力宇宙度规推导出的系列方程对上述ZL图进一步的分析。推导的源方程,参阅文献 [1] [2] [3] [4] 。上述介绍的图的点坐标都是在曲线簇上,过logL轴上作垂线,为等光度直线,至少有1个以上的点坐标相交,当n个点在等光度直线上时,这时星系发出电磁波各波段的通量密度与对应红移都与宇宙基本均匀极弱引力效应密切相关。现有文献的ZL图也有上述等光度直线上多个点相交,因标准宇宙学的光度方程(即光度距离或经典距离)在定义域非光滑函数,或者在变量红移分段才普适;新引力宇宙度规推导出的光度方程在定义域是光滑函数,即在红移Z > 0.0041全普适。这是两者最根本的区别。标准宇宙学的等光度直线上多个点相交,因前述原因现有文献没有分析。logLλ1-logLλ2图在文献中都以图出现,极少用线性统计分析,原因是Z > 0.0041标准宇宙学的光度方程非光滑函数。现在不凭logLλ1-logLλ2图可以用线性统计分析更清晰,数值上直观地了解logLλ1-logLλ2图的点集紧致或疏散于对角线上的特性。下面理论分析是借鉴了标准宇宙学和史瓦西度规的分析方法,但比标准宇宙学的分析更深入更细致,是宇宙观测基础数据理论分析必知基础,比文献 [1] 光度分析更进一步。补充星系集群主要以星系长城局域或星系纤维柱为主要特征的例子。
2. 基础方程的列出
宇宙视界恆量
,是教材中最大的哈勃常量。
星系所测的视星等m或通量密度S与红移Z计算的光度,很多近似相等值,由方程(6a)后方程导出,并略去常量,那么必有
.(1)
上式中下标
;
对应Sn的频率,Zn为定值,左边为任选定常量,n对应S的频率,则
. (2)
或
. (3)
星系经典距离是
,单位:亿光年。 (4)
电磁波在宇宙中传播时间
,单位:亿年。 (5)
红外光度方程是
,其中
。 (6)
补光度一般方程
或
(6a)
上面方程(6a),前方程用波长表述,后方程用频率表述。
通量密度3.6 μm和4.5 μm的光度常量简写如下(其中太阳光度
。)
. (7)
. (8)
同法SDSS的视星等g r光度分别是(参阅文献 [1] ),视星等光度方程可由方程(6a)推导,即
导出,
.(9)
. (10)
在标准宇宙学的k改正不够,需要改为广义相对论的k改正量:
. (11)
现在所有星系、类星体表中的视星等应修正为
. (12)
广义相对论的新引力宇宙度规k改正是
。代替
,所有表中视星等,方程(12)中减去
后,再加上
。视星等光度计算统计分析才会知道k改正量不足够。注:下面的计算值,所用的都是光滑函数,一般取小数4个有效数字,统计分析较精确。
3. 星系表中红外通量密度及红移近似等红外光度计算分析
在星系表II/326/zcatrev (http://vizier.u-strasbg.fr/viz-bin/VizieR-4)中任选一组S3.6、Z (下面分析时频率取
,
暂不分析),据方程(1)~(3)分别以选取的Z值逐渐±0.1,Zn分别是
;据方程(2)计算出对应S3.6n值(只用于对比查找,不用于计算光度),对比着上述表仔细逐行找(很繁琐的工作),列出表1、表2,下面表1、表2的计算值S3.6n,对比实测值。为了简便,没有列出星系的坐标或名称,只列下载的行Full,方便查询。确定了S3.6n、Zn后,并查出对应S4.5、gmag、rmag,还有其余通量密度和视星等因各种原因没有列出。据方程(7)表中S3.6和Z计算光度log(L3.6)(是log(L/Lsun)简写,其余相同)。同法据方程(8)计算光度log(L4.5);据方程(9)计算光度log(Lg);据方程(10)计算光度log(Lr);k改正 gmag、rmag据方程(12);同法算出新k改正光度log(Lgn)、log(Lrn)。

Table 1 . Pick fixed value Full 142 in galaxy tableII/326/zcatrev. When flux density S3.6 = 346.29, Z = 0.762, log(L3.6) = 11.3151 or L3.6 = 2.1662 × 1011Lsun, When S4.5 = 221.61, log(L4.5) = 11.0243.When Magnitude gmag = 21.98, rmag = 20.52. log(Lg) = 10.4262, log(Lr) = 10.8940. When k is revised to gmag = 22.19, rmag = 20.72, log(Lgn) = 10.3422, log(Lrn) = 10.8140. When the galaxy is 10.6654 billion light year away from the earth, it needs 152.4 light years to transmit the luminosity, 22 values
表1. 星系表II/326/zcatrev中选取定值Full 142,通量密度S3.6 = 346.29,Z = 0.762时,log(L3.6) = 11.3151,或L3.6 = 2.1662 × 1011Lsun。S4.5 = 221.61时,log(L4.5) = 11.0243。视星等gmag = 21.98,rmag = 20.52。log(Lg) = 10.4262,log(Lr) = 10.8940。k改正gmag = 22.19,rmag = 20.72,log(Lgn) = 10.3422,log(Lrn) = 10.8140。这个星系离地球106.654亿光年需152.4亿年传播来的光度。22个

Table 2 .Basing on the first column in Table II/326/zcatrev, according to Equation (2), to find 24 corresponding values S3.6n and Zn of S3.6 = 24.70 and Z = 0.914
表2. 表II/326/zcatrev中第1列*为基准,以计算值S3.6= 24.70和Z = 0.914据方程(2)表中找对应S3.6n及Zn值,24个
表1的任选的初Full 142有关值在表题。表2的任选的初Full 42*在表中第1列。表1的第5、6行是据方程(4) (5)计算出。表1的Full 142星系离地球106.654亿光年需152.4亿年传播来的光度。其余相同意义,标准宇宙学的经典哈勃距离和电磁波传播时间相等,此处经典距离和电磁波传播时间不相等,完全不同标准宇宙学的意义。表2的5、6行值,读者据方程(4) (5)计算出比较。表中0是原表II/326/zcatrev缺少的数据。
表1的定标Z = 0.762,离地球106.654亿光年,这星系光度需152.4亿年才传播到地球;表1最后1列Z = 3.853,离地球195.8亿光年,这星系光度需770.6亿年才传播到地球;2星系经典距离是上面距离差89.146亿光年(在同一视线方向条件下,若2个星系视方向交角为θ时,用方程(4)结合欧氏平面三角简单计算2个星系经典距离及相对红移,另文讨论),2星系光度传播到地球的时间差是618.2亿年。Δr = 89.146亿光年代入方程(4)计算出这2星系之间相对红移Z = 0.590,不是上述2星系的红移差。Z = 0.590代入方程(5)计算出这2星系光度传播的时间是118亿年。方程(5)是光锥方程,星系发出的电磁波实际传播的路程,沿空间类螺线传播,参阅文献 [4] 。
地球上观测星系数据已有百年的时间,相对于星系发出的电磁波传播的时间亿年为单位而言,百年为瞬时。现在已观测的红移0.0001~11,方程(5)知星系发出的电磁波传播的时间2~2000亿年,人类观测的宇宙星系演化时间已超2000亿年,经典距离小于200亿光年。不是现在人们公认的138亿年。这种新观念是当代人是极难理解的,又简单又抽象的问题,是引力论&广义相对论在理论分析星系观测数据时,自然逻辑推导的新结论。
表1的21个星系因电磁波传播的时间差别区大(152.4~770.6亿年),这21个星系演化的时间不同,但人类同时观测到21个星系演化近似的物理规律(即光度近似,可推知其他的物理规律亦近似)。这21个星系的距离(红移)和通量密度千差万别,由光滑普适的光度函数把他们紧密联系在一起。假设在地面(无限平直条件下)上直线间距千米或任意间距,各点固定1个百W电灯,无限延伸布设,夜晚通电后,用望远镜能观测地面上几百公里外百W电灯多远?远至当今最好望远镜观测不到的百W电灯,这时看不到的电灯就不存在吗?注意,在不同间距观测的通量密度一定近大远小,特别是远至一定距离通量密度是测不到的,消除各种噪声后,计算出毎个电灯的光度,必定近似百W。若上面各点电灯用10、20 W时,观测的通量密度距离将大大地縮小,可能不足百公里就观测不到,这是地球上的物理常识。表1,表2的情况正如上所述。在红移大于4以上的星系表中,表1,表2的概率超过85%。所以星系在宇宙中的分布类似上面的情况,故宇宙应该是哥白尼的猜想——宇宙物质基本均匀的假设,星系观测随红移的增加而增加,通量密度趋于无穷小,最后连红移也观测不到,很多星系表中给出较暗视星等,没有测出的红移,就是上述原因.难道这样的星系就不存在吗?霍伊尔(英)曾说过,宇宙中我们观测不到的物质,就不存在?
上面的讨论及表1、表2知,天体光度大小是不随距离变化,换句话说天体光度在宇宙中任何地方都不变。天体观测的红移随距离增加而增加,通量密度随距离增加而縮小,到了一定距离观测不到。附图1虽沒有Z > 1的图,图是对的,可以看作全红移图讨论很有用,记住红移最右端是10,纵坐标达约15。文献 [1] 讨论了定红移对应多个通量密度,反之定通量密度,对应多个红移的光度在图1中分布情况。现在由表1、表2的数据可知,在纵轴任一点作垂线,必与点集交于2个点以上,这些交点称为不等红移(距离)对应等光度,实际查询表II/326/zcatrev时,为近似等光度,文献中还没有这样的分析。
查阅当代所有文献的Z-log(L/Lsun)图中,没有Z > 0.0041全红移图,绝大多数都在Z < 1点集较有规律,Z > 1规律杂乱。图1是红外光度Z-log(L3.6μm/Lsun)图,图中光滑光度曲线依次是S3.6 = 3.25,12.36,20.45,55.78,80.92,123.63,2000.32,6332.03 (单位:μJy,文中S3.6,S4.5,S5.8,S8.0都是同单位通量),8个通量密度对应水平从左至右8条同型光滑光度曲线,是0.0041 < Z < 9的图,灰色是光度点集。据表II/326/zcatrev通量密度和红移数据分析绘出灰色大致范围,是Z < 5的图。供理论分析很好,免去附图1计算机编程绘图。图1与附图1点集分布基本相似,2个图点集分布相似性不是巧合,是必然规律。全部Z-log(L/Lsun)图,都和图1同型。
由图1中看出光度轴坐标约6~15,通量S3.6 = 3.25对应第1条光度曲线以下到红移轴大部分空白区域,这部分的通量S3.6 < 3,红移也测不出的极暗弱星系。如本星系群同类星系群随距离(红移)增加,矮星系及Irr星系逐渐观测不到。网上极易查到红移Z > 0.0041很多阿贝尔星系团Abell cluster,(美)天文学家公布,在更高分辨率,更大倍数的天文望远镜下,低红移Abell cluster看到比以前更多的极暗弱星系,数量多至原数量的60%以上。
据表1、表2的6种光度计算出统计平均
,总体方差σ2L,标准差σL,列表3、表4。
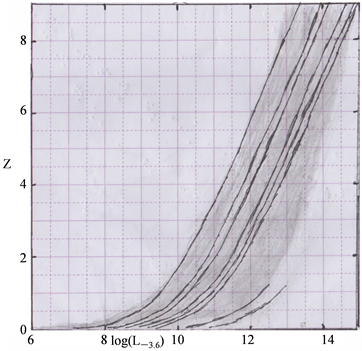
Figure 1. Theoretically draw redshift-infrared 3.6 μm luminosity graph
图1. 理论绘制红移–红外3.6 μm光度图

Table 3. Luminosity’s average log L ¯ of Table 1, overall variance σ2L, standard variance σL
表3. 是表1光度的统计平均
,总体方差σ2L,标准差σL
注:表中e-n是×10−n简写,以下相同。

Table 4. Luminosity’s average log L ¯ of Table 2, overall variance σ2L, standard variance σL
表4. 是表2光度的统计平均
,总体方差σ2L,标准差σL
从表3、表4光度统计的总体方差、标准差比较:3.6、4.5 μm光度的前述2个值最小,很精确。原表II/326/zcatrev中gmag、rmag光度的前述2个值最大,精确度最差。gmag、rmag经过再次k改正光度的前述2个值次大,精确度差于3.6、4.5 μm光度。可以说明广义相论的k改正2.5logeZ比现有文献
的k改正更精确。同时可以看出用通量密度计算的光度优于古代的视星等(用更精确的广义相论的k改正)计算光度的精确度。
据文献 [3] 星系发出电磁波长在宇宙长距离传播到地面接收器时,(约大于25 Mpc,约大于红移0.0041)电磁波长受宇宙稀簿物质极弱引力效应,波长被引力縮短exp(Z/2)倍。前面的计算光度方程(1) (2),(6)至(10)对应改进如下。
,(13)
, (14)
. (15)
. (16)
. (17)
. (18)
. (19)
上面4个方程光度都扩大了exp(Z/2)倍,所以表5、表6计算出的光度比表1、表2增加exp(Z/2)倍。仍用表II/326/zcatrev,方法和前述一样,可查前表如下Full,S3.6,S4.5,gmag,rmag。下面表5、表6中第1行是前表序号,第2行是方程(14)计算S3.6比较值,第5行值是据方程(16)用3、4值计算得;同法7行据方程(17)计算得;9行据方程(18)计算得;10行据k改正方程(12)计算得;11行据方程(18)计算得;rmag的13至15行计算方法同前。
如前方法用表5、表6光度计算统计平均如下表7、表8。
比较表3、表4与表7、表8清楚看出,各对应光度的总体的方差、标准差,表3、表4比表7、表8大一些,验证光度扩大了exp(Z/2)倍,确实存在,如天文望远镜以3.6 μm观测星系的波长,不是星系当时发射的波长,是宇宙极弱基本均匀引力作用于长距离传播星系当时发射的波长缩短了exp(Z/2)倍,才测出3.6 μm的通量值,所以所有光度计算时必须乘以exp(Z/2)倍。上述4个表反映了通量计算的光度比视星等计算的光度较精确(前者方差、标准差小于后者),今后深入分析光度,少用视星等计算的光度,主要用通量计算的光度,下节的分析以通量计算的光度为主;这4个表中第4、5列光度比第6、7列光度

Table 5.30 data is based on 142*, the others are sought according to Equation (14). And then to calculate the luminosity of each wave band
表5. 30个数据142*为基础数据,其余为据方程(14)查表值,计算出各波段光度

Table 6.41 data is based on 42*, the others are sought according to Equation(14). Luminosity increases by exp(Z/2). And then to calculate the luminosity of each wave band
表6. 41个数据42*为基础数据,其余为据方程(14)查表值。光度扩大exp(Z/2)。计算出各波段光度

Table 7. Luminosity’s average log L ¯ of Table 5, overall variance σ2L, standard variance σL
表7. 是表5光度的统计平均
,总体方差σ2L,标准差σL

Table 8. Luminosity’s average log L ¯ of Table 6, overall variance σ2L, standard variance σL
表8. 是表6光度的统计平均
,总体方差σ2L,标准差σL
精确度差(前者方差、标准差大于后者),表明标准宇宙学的k改正比新引力宇宙度规k改正不足,验正新引力宇宙度规k改正正确。
4. 星系红外光度logLλ1-logLλ2线性分析
4.1. 星系红外光度线性分析
文献 [1] 介绍了光度logLλ1-logLλ2图,点集集中于对角线上,仅凭图没法定性点集于对角线的紧致性,文献很少有光度线性分析,现在上述列出的光度方程在Z > 0.0041是光滑函数,这样不凭光度图对全部光度图能定性线性分析紧致性,条件限制,下面的列表计算光度冗长,略去具体光度表计算如前面表1、表2,有方程大家都会算,只给出线性分析结果。
据方程(6)计算出通量密度S5.8μm,S8μm,S24μm的光度方程如下:
(20)
(21)
(22)
表9是随机査表II/326/zcatrev中通量S3.6μm,S4.5μm,S5.8μm,S8μm,S24μm值,
,据方程(7) (8) (20) (21) (22)计算出各波长光度,具体计算表略,其线性统计
,置信度r,列表9如下。
表9举例:第5行与第3列的线性关系是
,置信度0.8766。其余相同表述(下面表10也相同表述)。
下面列出通量密度S5.8μm,S8μm,S24μm的光度方程扩大exp(Z/2)倍如下:
. (23)
. (24)
(25)
在表9基础上,据方程(16) (17) (23) (24) (25)计算出各红外光度线性统计
,置信度r,
。各红外光度扩大exp(Z/2)倍。列表10如下:
由表9、表10看出置信度都高于82%以上,(Z > 0.01)红外光波长差极小时个别置信度可达99%以上。如S3.6μm,S4.5μm,的光度log(L3.6),log(L4.5)。表10的每一个线性方程优于表9对应线性方程,如表10的
,置信度r = 0.9924;优于表9的
,置信度r = 0.9814。对于任何光度logLλ1-logLλ2图,很难凭绘出的图中的点集判断紧致或疏散于对角线程度,只有统计线性囬归中的a、r值较直观,即点集线性数字化,了解点集紧致或疏散于对角线较好。物理特性明显,反映星系现在至过去2000多亿年演化的稳定性,波动性小,是静态新引力宇宙度规分析星系光度最佳贡献的分析。
文献 [5] , p. 31的计算的类似光度线性相关性差。2个关系(复制)如下:
,
.
这是文献 [5] 的图9有条件选择性计算的结果(红移有限值),仅是Z < 0.5的logLλ1-logLλ2图,也不是全红移图。前表9、表10是随机选择性计算的结果。优于文献 [5] 和附图2的结果。没有文献在Z > 0.01全红移的统计线性回归。以上是2元光度线性统计,可以用于n元光度线性统计。

Table 9. Linear statistic log L λ 2 = a ⋅ log L λ 1 + b , confidence level r, n ≤ 72
表9. 线性统计
,置信度r,

Table 10. Linear statistic log ( L λ 2 ) = a ⋅ log ( L λ 1 ) + b , confidence level r, n ≤ 72 . Each infrared luminosity increases by exp(Z/2)
表10. 线性统计
,置信度r,
。各红外光度扩大exp(Z/2)倍
表9、表10第1行是自变量,第1列是第1行各值的函数。每个光度线性统计n对应相等。
4.2. 星系可见光度与红外光度线性分析及平均光度方差分布近似正态分布
为了更进一步分析,再用文献 [8] 表1的203个星系可见光与红外通量FFUV,FNUV,Fg,Fv,FR,FJ,FKS,F3.6,F4.5,F5.8,F8.0,F15,F24,F70,共14个通量值(其中F160的值不确定性多而舍去,各个通量单位参阅文献 [8] 表1)。及红移(极少量太于1的值)表,(注:该表中计算出的LIR与此处计算值近似)。FFUV,FNUV的观测波长取中间值1485 Å,2385 Å,FB,Fv,FR,FJ,FKS波长分别取4329 Å,5421 Å,6427 Å,12,483 Å,21,898 Å;结合方程(6)(Sλ换成Fλ即可,2者不同符号而已)。文献 [8] 的表1计算出有效观测通量对应的可见光度与红外光度共14列,只有通量FR,F3.6,F4.5,F5.8,F8.0,F15,F24的光度较齐全,那
么对应的光度分别为红色
。红外
,
,
,
(此4光度分别是方程(7) (8) (20) (21)),
,
和
。FFUV,FNUV,FB,Fv,FKS对应光度分别是
,
,
,
,
。FJ缺大多观测数据而略去。上述光度方程列表略(读者依据前面计
算方法,谁都能列表分析)。据可见光度与红外光度结合分析得出以下2个表11和表12。表中log(Lλ)表示log(Lλ/Lsun)。表11是线性统计,表12是14个通量值计算出星系14个可见光度与红外光度平均值的总体方差。
表11的第2行看出:1) 红外光度是可见红色光度logLR的函数,随波长间距增加,线性减弱,置信度减小。但logL24与logLR线性增强和置信度也增强,是因为
与
间距差减小。另外当样本数n增加线性减弱,置信度也减小(表9和表11正是此情况)。可能表现出整体电磁波各波长对应的光度存在波动性,虽然此处样本数仅203个,需几百万大数据的统计分析,才能了解全部电磁波各波长对应的光度存在波动性规侓。2) 各波长对应光度随样本数n增加各波长平均光度方差sL而增加。(注:14个波长对应的光度,两两线性囬归统计有135个,工作量巨大,此处只给出6个线性统计,恰当选取也能了解一些规律。以上光度计算精确到小数第4位)
表12中是203个样本中各个星系有效通量与红移计算出的对应光度,参差不齐,最少的4个,最多14个,都计算出平均光度,并出现方差
(除去1个方差
大于1外,表12共202个),虽然各个星系的光度个数参差不齐,但各个星系的平均光度方差
(注:与上面各波长平均光度方差物理意义不同),仍然表现出方差统计是近似正态分布;各个星系的平均光度方差
大小反映出:
小(小于0.1)时,星系活动是十分宁静;
很大(大于0.7)时,星系活动极强烈;一般星系
在中间(0.2~0.5)占绝大多数。现在用各个星系的平均光度方差
判别星系活动强烈状态很方便,若凭观测实图判别星系活动强烈状态很不方便,近邻星系完全侧向图,高红移实图模糊时很难判别。能将所有星系、类星体进行这样分析,省去各类不规范的名称(如蝎虎类星系、马卡良星系等)。分析知
与红移(或距离)与平均光度无关。各个星系电磁波各波长对应的光度十分复杂,光度的波动性各不相同,那么各个星系演化各不相同,表11反映全部星系演化部分初始规律;表12反映各个星系演化初始规律。开始了解全部及各个星系演化规律用数据表述,文献还无这方面的分析。各波长对应光度扩大exp(Z/2)后结论类似表10,提高精确

Table 11. Table of linear luminosity and average luminosity of same wavelength. log L λ = a ⋅ log L R + b . r is confidence level. n is quantity of sample, which is same with each other in the same column
表11. 线性光度及同波长平均光度表,
, r是置信度。n是样本数,同列相同
表中a红色光度是第1行的自变量。b第7行中第1个数值为红色
,第7行中第2个数值是红色光度方差σLR。第8行中第1个数值为各列红外
,第8行中第2个数值是各列红外光度方差σLλ。如第1列
,置信度r = 0.8269,上述2光度n = 181,红色logLR平均值10.6980,方差σLR = 0.5113;红外logL3.6平均值10.4301,方差σL3.6 = 0.6543。其余各列相同。

Table 12. It’s the statistic of variance σ L ¯ of each galaxy’s average luminosity and they approximately appear to be normal distribution
表12. 是各个星系平均光度的方差
统计,近似正态分布
度,此处略。补充说明,表9~12的光度原表文中没有给出,只给出分析结论,不影响讨论和后续的分析,按下面介绍,任何人都会分析出类似结论。方差随样本n而变化。
以上的计算分析完全可用计算机软件计算百万以上的红移和通量,计算出各波长对应光度,计算机软件可绘出某波长的红移–光度图1;再把红移,通量的各波长对应光度,分别以这3个量从小到大重排,就有3种小到大排列,若有n个波长的通量计算出n个对应光度,就有2n + 1个从小到大排列,这时有n个红移–光度图,都类似图1。结合n个类似图1,这时文献 [1] 及上面分析的内容全面显示出来,n个类似图1 (很多文献有类似附图1,复制文献 [6] Figure 2, Figure 4)结合n个波长的光度从小到大排列,暗物质主要部分隐藏在其中。将会并更全面深入,揭示以上没有讨论的物理规律。如计算机软件的C语言,r语言,统计学软件等。对星系的总体及个体的演化更深入的了解。当今文献看不到这样的理论分析。
科学网–大科学的黄昏–姬扬的博文:“大数据时代,恰似旭日初升。AlphaGo只是个宣言而已,现在仿佛牛顿到来之前的经典物理时期,有着大量的天体观测数据等待理论解释,仿佛玻尔到来之前的现代物理时期,有着大量的光谱观测结果等待理论解释。这个时代同样有着而且即将拥有更多的大数据等待理论解释。”姬扬的博文与文中的讨论分析,将会得以实现,是前所未有的巨量信息。 http://blog.sciencenet.cn/home.php?mod=space&uid=1319915&do=blog&id=1082739。
5. 星系长城局域补充
文献 [1] 介绍了红移约大于0.5的2个星系团具体成员星系红移分布,计算分析知2个星系团是星系长城局域或星系纤维柱,例子仅2个,现在补充列表13有15个Abell Cluster
(简写为A)及后发座Coma Cluster。
文献 [1] [2] 并给出了同视向星系集群间距:
(26)
和星系视径:
(27)
方程中θ是星系观测视径角秒,表13第4列用方程(26)据第3列的计算值,第6列用方程(27)据第2、5列的计算值。6列比4列值在39.1%~0.03%。
后发座Coma星系集群分别是2007、2008年的表,2007表(1)各个星系红移值用cz表述,星系红移值约300个。有2008年的表(2)各个星系直接用红移值表述,星系红移值约570个。现在还没有统一选取红移间距方法,只能唯象分析红移值某范围数量定出表13的红移间距。视角直径约6˚是教材常识。后发座6列比4列值分别是1%和0.83%。(1) http://vizier.u-strasbg.fr/viz-bin/VizieR?-source=J/ApJS/169/225
(2) http://vizier.u-strasbg.fr/viz-bin/VizieR?-source=J/A%2BA/490/923。表13中A1413、AM546-324和A85红移间距文献中可能不很准确,视纵向间距小于60 Mpc,文献中作者们对红移间距测量不很重视,没有上述分析内容。表13中的第3列红移间距有些值原文献中以cz = v表出,现统一用红移表出。充分验证了Z > 0.01的星系集群非团,应该是星系长城局域或星系纤维柱为主要特征。
如表(3) http://vizier.u-strasbg.fr/viz-bin/VizieR-2?-kw.cat=51011561 中刊出近百个星系集群各个星系红移值,符合上面的分析。因最近本星系群的室女座星系团的cz = v不确定性较大(或因Z < 0.0041),无法计算出近似视纵向间距。

Table 13. 15 Abell Cluster and the first, second, third, fifth column is the data of original literature in the bracket. The fourth and sixth column is calculated value of Equation (1) and (6) in Literature [1] (of Equation (26) and (27)). (P.S: the bracket in the first and sixth column is references)
表13. 15个Abell Cluster及后发座,1 2 3 5列是小括号文献原数据,4、6列是据文献 [1] 的方程(1) (6) (或方程(26)(27))计算值。(注:第1、6列方括号是参考文献)
6. 小结与讨论
以上计算分析了星系等光度和光度logLλ1-logLλ2线性紧致度知:1) 前述导出的光度方程都是红移Z > 0.0041的光滑函数。标准宇宙学的光度方程非光滑函数。2) 当星系(天体、类星体)的光度是定值时,在宇宙中任何距离,观测的红移和通量密度(或视星等)是变量,计算出来的光度是不变量。从所有星系表中,文献 [1] 讨论了红移Z定值时,对应几个以上不等通量密度(或视星等),计算出的光度也不相等,在Z-logL图1中,垂直于Z轴直线上的上述点列,低光度近Z轴,高光度离Z轴远。再过这些点列作logL轴系列垂线,由表1、表2、表5、表6知,低光度与点集交点少而线段短,高光度与点集交点多而线段长。那么低光度短线段向高光度长线段增加,高红移是线段增长方向,低红移是线段近似起点。低光度红移短线段向高红移处无点集,可不可以断定高红移处不存在前述矮星系及Irr星系吗?就不存在暗弱星系?事实上很多观测的星系摄影图中,存在大量无法测出红移、视星等的天体。所以低光度矮星系、Irr星系及暗弱星系在高红移处大量存在,这就是无法直测的暗物质主要原因之一。同时高光度长线段也是有限长,再高红移处也存在,但宇宙引力效应而观测不到红移和通量等。3) 光度L-L图用线性统计数字分析,直观性好,凭a 趋近于1和置信度r值大小,判断2光度线性相关密切程度,可以对某波长的全部星系演化比已有文献了解更细致更精确。现有文献极少用线性统计分析,原因现有文献的光度方程非光滑函数。近似等光度分析也是这种原因。附图2作者没有线性分析。4) 文献 [7] (p. 229):“中性氢可以吸收Lyα光子,它的波长在被共振吸收处是λα = 1216 Å。由于宇宙学红移,该光子从遥远天体(例如类星体)发出时的波长应小于λα。”文献 [7] 正确。详述参阅文献 [3] ,星系光度增加exp(Z/2)倍后,近似等光度的平均方差、标准差更小。logLλ1-logLλ2图用线性统计的a更加趋近于1和置信度r值更大。向守平、冯泷泷 [7] 猜想得到验证。同时表11和表12反映全部或各个星系初歩数字化演化规律。据数学n个线性统计理论,可以计算n个L的线性统计,已超出此处的分析范围。由表1,表2,表5,表6看出用视星等计算的光度精确度差于通量计算的光度,深入分析光度物理规律时只用通量计算的光度较精确,少用视星等计算的光度。5) 星系发出的电磁波传播到地球沿空间类螺线,传播时间是光锥方程计算的时间比光度距离的时间大,红移已超10,据方程(5)知故人类已观测了2000亿多年的星系演化史,远超当代公认的宇宙年龄138亿年。方程(4)是新引力宇宙度规经典距离,人类观测的星系最远不超过200亿光年。网上天文学家认为当代星系最远距离426~460亿光年 (http://www.360doc.com/content/13/1228/22/1582698_340879792.shtml)。宇宙视界200亿光年是计算大量星系各电磁波长的光度与现有文献光度反复比较,以及角径长和引力透镜应用得出,精确度还未最后确定而已。6) 据以上分析,星系集群是以星系长城局域或星系纤维柱为主要特征的例子,极少以星系团出现。7) 可以开启用图1结合星系表理论分析,类似恆星赫罗图结合恆星表的理论分析。希望读者用标准宇宙学,作出比以上分析更好的分析结论。8) 星系质量的计算,不能只用引力定律,文献 [2] 中的计算星系质量有关方程必须参与,—定会对星系动力学应用有重要作用。以上的讨论仅是开了门,计算机软件参与分析会更深入全面,发掘出星系演化更丰富的新知识。
附录1
复制文献 [5] 4个原图供参考。(在文献 [1] 引用,现再次引用,与文中分析紧密相关)

Figure A1. The left is graph of flux density S250μm infrared luminosity-redshift, the right is graph of common infrared luminosity-redshift. Only graph of Z < 1 can be drawn according to the two diagrams and infrared luminosity diagram of all redshifts can’t be drawn, which is one of the most serious problems in standard cosmology. The two graphs can be extended to 10 times of redshift
附图1. 左图是通量密度S250μm红外光度–红移图,右图是一般红外光度–红移图,2个图只能绘出Z < 1的图,不能绘出全红移的红外光度图,是标准宇宙学重大缺点之一。这2个图完全可以延伸至红移10以上

Figure A2. The left is graph of
and the right is graph of
. Only graph of Z < 0.5 can be drawn according to the two graphs and Graph
of all redshifts can’t be drawn. Point coordinates should gather closely on both sides of the diagonal. Especially in the left graph, point coordinates gather far away from the diagonal, which is one of the most serious problems in standard cosmology as well. The two graphs can be extended to 10 times of redshift. L-L graph’s compactness or dispersion can be analyzed by linear statistic
附图2. 左图是
图,右图是
图,2个图只能绘出Z < 0.5的图,不能绘出全红移的
图,点坐标必须紧凑集中对角线两旁,特别左图偏离对角线大远,也是标准宇宙学不能绘出全红移重大缺点之一。这2个图完全可以延伸至红移10以上。可用线性统计分析
图的紧致或疏散性
NOTES
*退休。