1. 引言
随着科学技术的飞速发展,市场竞争也越来越激烈,产品的定价因为涉及到所有社会成员的利益而具有强烈的现实意义。企业根据想实现的经营目标来解决产品的定价问题,有些企业的经营目标是实现自身利润最大化,T. Maiti [1] 研究了在涉及回收的双向闭环供应链中各个经营者为实现自身利润最大如何决策定价的问题;有些企业的经营目标是占有市场或者实现相对利润最大化,Ting Li [2] 中一个制造商以市场份额(目的是占有市场)为经营目标。A. A. Elsadany [3] 研究的是在相对利润最大化的基础上带有有限理性的古诺寡头博弈动力系统。另一方面,由于竞争越来越激烈,供应链(SC)的角色也承受了一些重大变化,制造商不仅要满足零售商的需求,还要保证供应产品的质量,质量差的产品会影响公司的销售额。再者,产品质量对于已经支付高价格的消费者同样重要,他们期望高质量,如果没有达到要求,他们就会从竞争对手那里购买,从而对制造商、零售商的效益产生影响。因此,产品质量水平在供应链中是个很重要的因素。J. X. Chen等 [4] 研究了一个制造商和一个零售商在双渠道集中和分散两种决策下的价格与质量决策。Y. Xie等 [5] 研究了包含一个供应商和多个零售商的两级供应链的价格决策,零售商尽自身最大努力水平使制造商进行质量提升。B. C. Giri [6] 研究了多个制造商和一个零售商在两级供应链的价格和质量决策。
本文受以上文献启发,研究不同经营目标下考虑质量水平的供应链定价博弈,解决两个具有竞争关系的制造商和一个零售商构成的两级供应链的定价问题。运用Stackelberg博弈求出了该模型的最优定价与最优利润,并进行比较,最后数值模拟质量水平对批发价、零售价的影响。
2. 问题描述及符号
本文研究一个包含两个具有竞争关系的制造商(分别记作制造商A和制造商B)和一个零售商的供应链,制造商A和制造商B生产不同质量水平的同类产品。制造商A生产质量水平为
的产品,制造商B生产质量水平为
的产品(其中
) [3] ,并分别以批发价
批发给零售商,零售商再以
的零售价销售给消费者。模型如图1所示。
需求函数通常假设是线性的,Y. Xie [5] 、张铁柱 [7] 及J. Zhao [8] 中需求函数为价格的线性形式;R. D. Banker [9] 中需求函数为价格与质量的线性组合。本文假设产品的需求
是产品的质量水平(
)和零售价(
)的线性形式
,市场需求函数设为:
(1)
(2)
这里
表示需求
对产品i的零售价的敏感系数,
表示需求
对产品i的质量水平的敏感系数,其中
,即产品i的需求受零售价
和质量水平
的影响大于受产品j的零售价
和质量水平
的影响
。
本文假设质量提升成本函数为
,二次式表示收益递减,即产品质量从87%到89%的增
长通常需要比从85%增长到87%更大的增量投资 [9] [10] [11] 。为了计算简便,忽略其他与质量无关的生产成本,这不会改变模型管理见解的主要结果 [4] 。
制造商A的利润为
(3)
制造商B的利润为
(4)
零售商的利润为
(5)
3. 模型求解与分析
考虑Stackelberg博弈,制造商A、B是领导者,零售商是跟随者。两个制造商采取两种不同的经营策略:一,制造商A、B同时决策批发价,使自身利润最大化;二,制造商A、B同时决策批发价,决策的目标是使相对利润最大化。在这两种策略下,两个制造商首先公布产品的批发价,零售商看到批发价之后再来设定产品的零售价。
3.1. 以自身利润为经营目标
本节考虑两制造商的经营目标是使自身利润最大化的策略。在Stackelberg博弈下,首先制造商A、B同时决策批发价
,使自身利润
最大化,然后零售商决策零售价
。
的Hessian矩阵为
(6)
因为
。所以Hessian矩阵负定。此时零售商的利润是凹的并且存在唯一的最优解。
关于
的一阶偏导数
其中
。
由一阶导条件,可得
(7)
(8)
将
,
代入(3),(4),求解
可得
(9)
(10)
将(9),(10)代入(7),(8)得
将
,
,
,
代入(3)、(4)、(5)可得制造商最优利润、零售商最优利润:
定理1. 质量水平
对批发价
,零售价
的影响如下:
1) 批发价
、零售价
随质量水平
的增加而增加。
在渠道参数满足
(
)时随
的增加而降低(增加)。
在渠道参数满足
(
)时随
的增加而降低(增加)。
2) 批发价
、零售价
随质量水平
的增加而增加。
在渠道参数满足
(
)时随
的增加而降低(增加)。
在渠道参数满足
(
)时随
的增加而降低(增加)。
证明:
(1)
当
时,
当
时,
当
时,
当
时,
由此定理得证。
(2)
当
时,
当
时,
当
时,
当
时,
定理得证。
3.2. 以相对利润为经营目标
本节考虑以相对利润为经营目标的策略。一个行业的公司不仅追求提高自己的业绩,而且还希望超越竞争对手的公司,这种行为的例子非常普遍,例如:电视观众评级竞争和啤酒厂、汽车制造商、便利店连锁店和手机运营商的市场份额竞争等等 [12] 。因此,相对利润最优是一些企业追求的目标 [13] [14] [15] ,参与者的相对利润可定义为其绝对利润与其他剩余参与者平均利润的差 [3] 。制造商A的相对利润记为
,制造商B的相对利润记为
,两制造商的相对利润分别为:
(11)
(12)
两制造商通过选取适当的
使相对利润最大,之后零售商决策最优零售价
。由(6)式可知,零售商存在唯一最优解(7),(8)。将(7),(8)代入(11),(12),求解:
可得
(13)
(14)
其中
,保证
有意义。
相应的,可得零售价的最优解:
将
,
,
,
代入(3)、(4)、(5)及(11)、(12),可得制造商利润、零售商最优利润及制造商最优相对利润:
定理2. 批发价
、零售价
均随着质量水平
的增加而增加,而批发价
随着
的增加而降低。零售价
在渠道参数满足
(
)时随着
的增加而增加(降低)
。
证明:
当
时,
当
时,
当
时,
当
时,
定理得证。
比较两种经营策略,可得以下定理:
定理3. 以自身利润为经营目标策略下的批发价
、零售价
高于以相对利润为经营目标策略下的批发价
、零售价
。
证明:
定理得证。
定理4. 以自身利润为经营目标策略下的制造商的最优利润
高于以相对利润为经营目标策略下的制造商的最优利润
。零售商的最优利润则相反,即
。
证明:
定理得证。
4. 数值模拟
本节基于实际的竞争,选择一些对应的参数值。利用数值模拟来表明两种策略下,质量水平对批发价、零售价的影响。
图2表明批发价
随着质量水平
的增加而增加。当渠道参数满足
时,
均随着
的增加而减少,但
减少的幅度小。当渠道参数满足
时,
随着
的增加而增加,
随着
的增加而减少。
图3表明零售价
随着质量水平
的增加而增加。当渠道参数满足
时,
均随着
的增加而增加,但
增加的幅度大。当渠道参数满足
时,
均

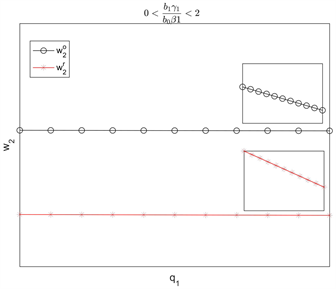
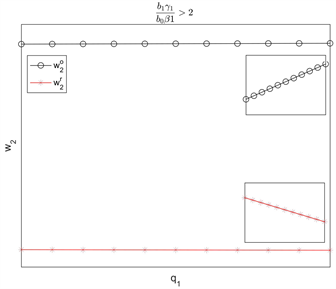
Figure 2. The effect of q1 on wholesale prices. (The small image is an enlarged view of the figure)
图2. q1对批发价的影响(小图是该图的放大显示)
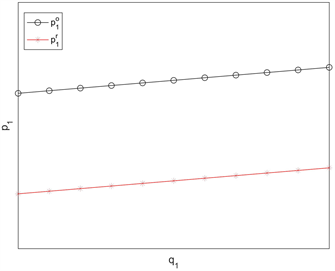
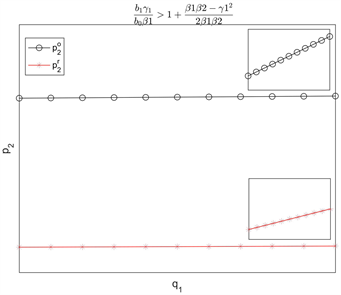


Figure 3. The effect of q1 on retail prices
图3. q1对零售价的影响
随着
的增加而减少,但
减少的幅度小。当渠道参数满足
时,
随着
的增加而增加,
随着
的增加而减少。
图4表明批发价
随着质量水平
的增加而增加。当渠道参数满足
时,
均随着
的增加而减少,但
减少的幅度小。当渠道参数满足
时,
随着
的增加而增加,
随着
的增加而减少。
图5表明零售价
均随着质量水平
的增加而增加。当渠道参数满足
时,
均随着
的增加而增加,但
增加的幅度大。当渠道参数满足
时,
均随着
的增加而减少,但
减少的幅度小。当渠道参数满足
时,
随着
的增加而增加,
随着
的增加而减少。

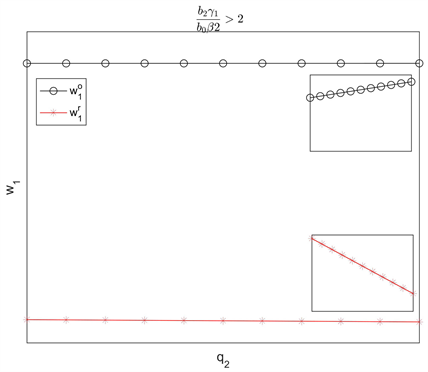

Figure 4. The effect of q2 on wholesale prices
图4. q2对批发价的影响



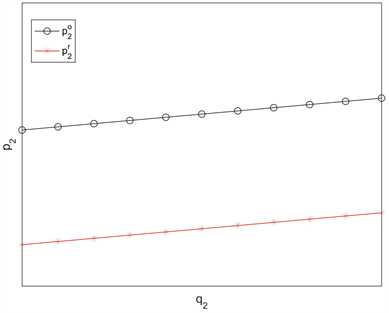
Figure 5. The effect of q2 on retail prices
图5. q2对零售价的影响
5. 结论与展望
本文主要研究不同经营目标下考虑质量水平的供应链定价问题。两个制造商和一个零售商参与供应链,制造商同时决策各自的批发价,零售商决策产品的零售价并向市场上的消费者销售产品,产品需求受零售价与质量水平的共同影响。考虑制造商Stackelberg博弈,比较两制造商以自身利润为经营目标和以相对利润为经营目标两种策略,结果表明:以自身利润为经营目标策略下的批发价、零售价以及两制造商的利润均高于以相对利润为经营目标策略下的值,零售商的利润则相反,即以相对利润为经营目标策略下的零售商的利润高于以自身利润策略下的零售商的利润。
本文研究的是在确定性需求下,质量水平为定值情况下的模型。可以延伸考虑质量水平为决策变量的情况或者考虑随机需求。此外,具有相同或不同定价策略的多零售商情况也可被视为当前工作的延伸。
符号
:产品i的基本市场规模
:自身价格敏感系数
:自身质量水平敏感系数
:两种产品之间的品牌渠道的交叉价格敏感性
:两种产品之间的品牌渠道的质量水平敏感性
:产品i的需求
:单位产品i的批发价
:单位产品i的零售价
:产品i的质量提升成本系数
:产品i的质量水平
:制造商A的利润
:制造商B的利润
:制造商A的相对利润
:制造商B的相对利润
NOTES
*通讯作者。