1. 引言
局部放电既是引起变压器绝缘劣化的主要原因,又是绝缘劣化的重要征兆。局部放电的检测是对电力设备进行各类试验的重要内容,而对局部放电的准确定位关系到更精确地反映设备的绝缘状况并制定相应维修策略,因此对局部放电进行定位具有重大意义 [1]。
针对于目前最广泛应用的局部放电的声学检测,现实可行的主要定位方法是超声波定位法,即根据局部放电产生的超声波的传播时延或波束方向来确定放电点的位置。近年来国内外学者针对基于超声波检测方法的局部放电源定位已展开了大量的研究 [2] - [12]。近年来,随着局部放电检测定位方法的发展,逐渐将阵列技术引入局部放电定位中。采用小型传感器阵列检测局部放电超声信号,并根据阵列信号理论来估计局部放电源的波达方向(direction of arrival, DOA) [13] [14] [15]。这种方法具有抗干扰能力强、信号增益强、空间超分辨能力高、波束控制能力灵活及定位精度高等优点,还可以实现多局部放电源的检测和定位。
MUSIC算法作为目前发展成熟、应用广泛且最具代表性的基于高分辨率空间谱估计定位算法,通过提取空间特征值信号子空间和噪声子空间的正交性,声信号阵列测向谱峰空间二维并行搜索声源的位置 [7] [16]。MUSIC算法能有效地对变压器高低压绕组匝间局部放电进行有效测向,但由于单个传感器阵列无法定位。满足交叉定位的最少的传感器数量为两个,但变压器内部结构紧凑,且如果再增加传感器阵列个数,对信号采集设备要求高,后续处理计算设备难以满足实时性,经济成本也过高,难以在实际环境中广泛应用。SRP声源定位算法定位精度高,对分布式传感器阵列实用性,适用于油中局部放电的定位 [17]。但SRP定位算法需要多次迭代,有一定的随机性,搜索空间越大,误差越大,且搜索空间中变压器内部结构复杂,会进一步影响定位精度。
本文提出基于MUSIC与SRP相结合的变压器局部放电故障定位方法。SRP定位算法与MUSIC测向算法有各自优势,本文所提出的MUSIC-SRP结合算法具备两者的优势,算法定位精度高。其原理是首先对变压器内高低压绕组匝间局部放电进行MUSIC算法测向,测向结果考虑误差范围可确定SRP算法的搜索空间,该搜索空间较小,SRP算法能够有效地对局部放电进行准确定位,获得局部放电源位置。利用研制的光纤超声传感器阵列,通过仿真和实验对该方法的有效性进行了验证。
2. 阵列定位算法
2.1. 基于MUSIC算法的超声测向方法
设K个远场信号入射到某阵列上,其中阵列由M个阵元组成,阵列接收的信号为:
式中:
X(t)是传感器阵列接收信号,
,
S(t)是信号向量,
,
N(t)是噪声向量,
,
为信号的方向矩阵,
表示方位角,
表示俯仰角,用
表示信号的DOA,
,
其中,
是来向为
的信号的方向矢量:
,
。
其中f是信号频率;
,rm是第m个阵元的坐标;ki是来向为
的信号的波数矢量,
。
MUSIC算法的基本思想是对阵列信号的协方差矩阵进行特征分解,根据噪声子空间与信号方向矢量的正交性估计DOA :
定义阵列输出信号
的协方差矩阵为:
其中,
,R是正定Hermitain矩阵,所以,
其中,
是信号子空间,
是噪声子空间,
和
分别是对应的对角阵。由于信号子空间和噪声子空间是相互正交的,可以得到:
,
其中
。
并且得到空间谱函数:
由上式,使
和
变化,通过寻找波峰来估计波达方向DOA。MUSIC算法测向谱图和等高线图如图1所示。
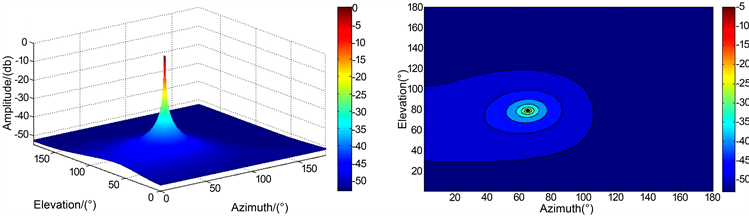
Figure 1. MUSIC direction-finding spectrum and contour map
图1. MUSIC测向谱图和等高线图
采用MUSIC算法首先应计算阵列输出信号X(t)的协方差矩阵R,实际上R用一定长度信号序列的一阶原点矩近似:
2.2. 基于SRP算法的超声定位方法
假设传感器阵列中第m个传感器和第n个传感器接收到的信号是xm(t)和xn(t),xm(t)和xn(t)的互相关函数为:
式中
为基本互相关时延估计算法,在噪声较小环境下具有较高的时延估计精度。但在环境噪声和混响较为严重情况下,基本互相关时延估计算法不再适用。因此在基本互相关函数法的基础上引入了一个加权函数提出了广义互相关函数法 (Generalized Cross Correlation, GCC),则xm(t)和xn(t)的广义互相关函数定义为:
其中,
为加权函数,Xm(w)和Xn(w)是xm(t)和xn(t)的傅里叶变换,( )*为取共轭。
为超声波从局放源s传播到第m个和第n个传感器的时间差。
加权函数
采用了GCC中常用的时延估计中相位转换加权函数,具体形式为:
取值为第m个传感器和第n个传感器接收到信号幅度谱的倒数,实际上是一个白化滤波器,能够白化互功率谱,使信号互相关的幅度谱信息得以保留并平滑信号间的互功率谱,提高定位精度。
在近场条件下其计算方法为:
其中rs为局放源s的空间坐标,rm和rn分别为第m个和第n个传感器的空间坐标,v表示超声波在油中的传播速度,
表示矢量2-范数。
可控响应功率SRP函数是根据所有传感器的广义互相关函数求和计算得到的,因此z处的可控响应功率SRP表达式为:
SRP不仅可以看作是加权的滤波-求和的波束形成,还可以看作是所有传感器对的GCC之和,具有稳健性 [18]。
局放源位置估计就是在空间内搜寻可控响应功率取最大值所对应的位置。
2.3. MUSIC与SRP相结合的局部放电定位方法
MUSIC测向算法对变压器内高低压绕组匝间局部放电测向时误差较小,适用性较强,可以将SRP的搜索空间合理有效地限定在某一较小范围内。SRP定位算法作为典型的分布式阵列传感器定位算法,可以在搜索空间较小情况下,对空间任意一点进行准确定位。MUSIC-SRP算法结合两种算法的优点,能显著提高局部放电定位精度,核心是利用MUSIC测向算法合理有效地将SRP的搜索空间缩小,使定位精度提升。利用图2分析MUSIC测向算法缩小SRP搜索空间的原理,建立变压器xoz平面坐标系如图3所
示。首先对局部放电点
进行MUSIC算法测向,得到俯仰角和方位角
。当变压器高压绕组匝间发生局部放电时,设内高压绕组内径为r1,高压绕组外径为r2,变压器顶部中心到传感器阵列中心距离为d。如图2所示,由于局部放电发生在高压绕组匝间,所以局部放电点i的zi的范围
为
,即
。考虑MUSIC测向算法在对方向角θi在90˚附近侧向估计时有微小误差,所以将[89˚, 91˚]区间作为分隔xi在正负半轴范围。如果
时,可根据图2几何推导出xi 的范围为
;如果
时,同理可推导出xi的范围为
;如果
,该传感器阵列在该范围MUSIC测向误差较小,考虑3˚测向误差余量,可根据空间几何关系得到xi的范围为
。对本文所用的35 kV变压器单相绕组,yimax为绕组高度与传感器阵列到绕组距离之和为70 cm,因此xi的范围为[−3.7, 3.7] cm。
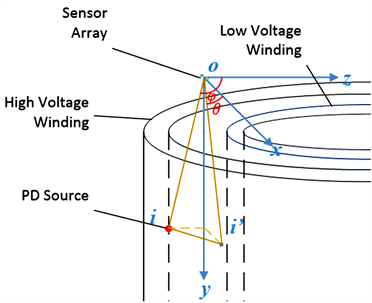
Figure 2. Schematic diagram of MUSIC direction finding for turn to turn partial discharge of transformer high voltage winding
图2. 变压器高压绕组匝间局部放电MUSIC测向示意图
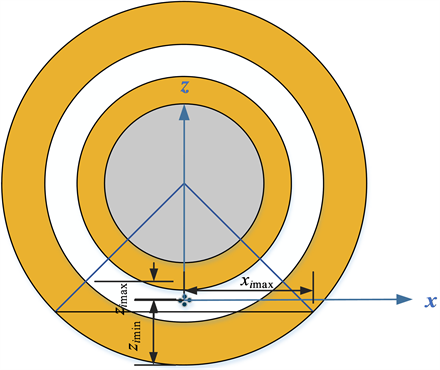
Figure 3. Transformer xoz plane coordinate system
图3. 变压器xoz平面坐标系
相对于局部放电点i的xi和zi坐标的范围确定,yi,坐标的范围确定较为复杂,利用数学几何的方法对局部放电点i的yi,坐标的范围进行详细求解。简化图2得到图4便于分析。如图所示,i'点为i点在xoy平面上的投影,k点为i点在y轴上的投影。目前已有局部放电点的俯仰角、方位角
和zi坐标的范围信息,即
,
,
,需要求解ok即yi,坐标的范围。由于的范围是由xi坐标的范围较为复杂,过程中包含了θi的误差余量。为了减少累积误差,所以通过zi坐标范围信息确定yi,坐标的范围。
因为
,所以
,因此
。考虑MUSIC测向存在一定误差,通过仿真结果可以看出
测向估计结果误差小于8˚,为了防止特殊情况导致误差过大,选择±10˚为误差余量。坐标yi的范围为
。如果
绕组高度与传感器阵列到绕组距离之和(70cm),那么yi的取值范围上限取绕组高度与传感器阵列到绕组距离之和70 cm;如果
传感器阵列到绕组距离(10 cm),那么yi的取值范围下限取传感器阵列到绕组距离(10 cm)。
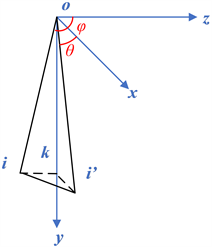
Figure 4. Simplified diagram of MUSIC direction-finding
图4. MUSIC测向简化图
3. 仿真研究
3.1. 仿真模型
利用COMSOL软件的声学仿真元件建立与实际实验环境相近的仿真模型。声场中描述流体微小声波的基本方程有运动方程、质量守恒方程、物态方程组成,因此理想流体介质中小振幅的声波方程为:
式中p为声压变化量、v为质点速度、
为密度变化量、T为温度变化量、v为拉普拉斯算子。该式表示为声压在声场中的时间和空间的变化规律。
构建一个变压器油箱及绕组仿真模型如图5所示。变压器油箱尺寸1 m × 2 m × 1 m。本文研究对象为变压器内部高低压绕组匝间局部放电,因此仅建立单相变压器绕组模型即可,选取的单相变压器绕组模型为35 kV某型号双绕组变压器,其几何参数为:绕组高0.6 m,高压绕组外径为0.25 m,内径为0.19 m,低压绕组外径为0.13 m,内径为0.1 m,铁芯半径为0.1 m,高度为0.6 m。仿真构建的变压器绕组模型,其主要结构包括高低压绕组以及铁心,各个材料物理属性按照表1设置。

Figure 5. Simulation model of transformer oil tank and winding
图5. 变压器油箱及绕组仿真模型

Table 1. Material physical parameters
表1. 材料物理参数
构建仿真模型时,需要选取合适的声源函数模拟局部放电点发出的超声信号。根据局部放电发声原理可知,局部放电时气泡的震动属于欠阻尼震动,因此建立了时域仿真的声源模型,欠阻尼的震动的公式为:
式中:A是电脉冲幅值,
是时间常数,f是放电信号的振荡频率。
由于实验所用光纤FP传感器的中心频率为30 kHz,因此本文声源函数中频率 取30 kHz,幅值A取为1,时间常数
取为1/(36000),声源函数波形如图6所示。
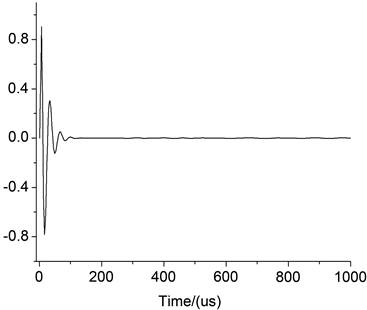
Figure 6. Simulation waveform of partial discharge function
图6. 局部放电源函数仿真波形
在进行网格剖分时,需要考虑相应材料的属性。由于主要关心超声信号在绕组内部的传播规律,因此进行有限元网格剖分时最大网格尺寸设置为超声在变压器油中波长的五分之一,最小尺寸为超声在变压器油中波长的十分之一。计算时间为1000 μs。
3.2. 空间坐标系的建立
本文中用四个光纤FP传感器采集局部放电信号。四个传感器嵌在模具上,排列方式为十字逆时针排列如图7所示。模具正中心到各个传感器探头中心点为0.9 cm。以模具中心点作为三维坐标系原点o(0, 0, 0),四个传感器探头处于xoz平面内,一号和三号传感器探头位于z轴上,二号和四号传感器探头位于x轴上,四个传感器探头坐标分别为(0, 0, 0.9)、(0.9, 0, 0)、(0, 0, −0.9)、(−0.9, 0, 0)。将局部放电源与z轴的夹角定义为俯仰角,用符号φ表示;将局部放电源在xoy平面上的投影与x轴夹角定义为方位角,用符号θ表示。因此波达方向DOA表示为(θ, φ)如图8所示。

Figure 7. Fiber optic FP sensor array
图7. 光纤FP传感器阵列
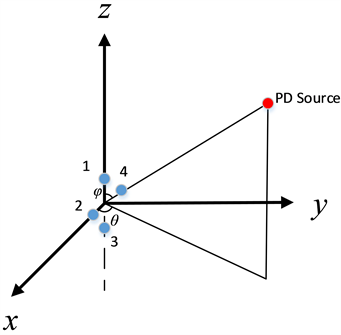
Figure 8. Three dimensional coordinate system of space
图8. 空间三维坐标系
本文针对变压器高低压绕组匝间局部放电检测,为了使传感器接收到的局部放电信号波形衰减和变化最小,将传感器阵列(观测点)设置在变压器高低压绕组间油道的正上方10 cm处,如图9所示。当低压绕组匝间发生局部放电时,局部放电信号在匝间反射后传播进入油道后,不需穿过任何介质即可被传感器接收;当高压绕组匝间发生局部放电时,局部放电信号只需穿过高压绕组油道一侧的绝缘纸板,即可被传感器接收。因此,将传感器阵列设置在变压器高低压绕组间油道的正上方,可以有效地将传感器接收到的局部放电超声信号衰减和变化最小。计划利用四个传感器阵列在油道中间隔90˚布置,实现对整个变压器高低压绕组匝间局部放电进行监测。单个传感器阵列需要观测的是90˚范围,即传感器高低压绕组的四分之一。
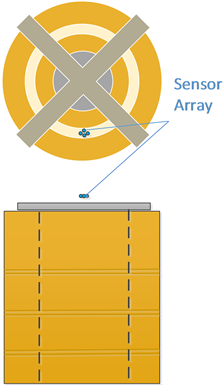
Figure 9. Top view and main view of relative position of sensor array and transformer winding
图9. 传感器阵列与变压器绕组相对位置俯视图与主视图
3.3. 局部放电点设置
对变压器高低压绕组匝间放电进行仿真,要在高低压绕组匝间分别进行多次是局部放电仿真。为了检验一个光纤FP传感器阵列所能监测局部放电的范围,需要在变压器绕组的不同深度和偏离传感器阵列不同角度上设置多个局部放电点并依次进行仿真。在深度为10 cm的上层绕组、深度为30 cm的中层绕组和深度为50 cm的下层绕组分别在高低压绕组匝间设置三组不同深度的仿真组,如图10所示,该图为变压器绕组纵截面的左半侧示意图。定义局部放电点以变压器铁芯顶部中心为圆心偏离1、3传感器连接线的角为偏离角,下文偏离角同义。高压绕组的宽度较宽,而低压绕组的宽度较窄,因此在偏离角为0˚、15˚、30˚、45˚的线上在高压绕组匝间设置三组不同匝间深度(2 cm、3 cm、4 cm)仿真组,在低压绕组匝间设置两组不同匝间深度(1 cm、2 cm)仿真组。如图11所示,该图为变压器的俯视图。由于传感器阵列设置在变压器挡板的角平分线上,只需设置右侧偏离传感器阵列不同角度的仿真组,而左侧的偏离传感器阵列不同角度的仿真组与右侧仿真组对称,理论上仿真结果一致,不需设置左侧仿真组。
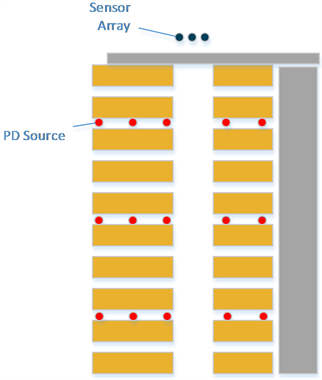
Figure 10. Setting of partial discharge points in different depths
图10. 不同深度的局部放电点设置
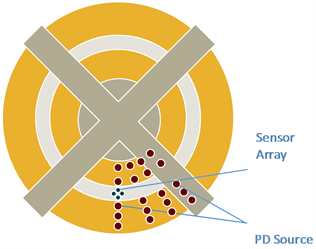
Figure 11. Setting of partial discharge points with different deviation angles
图11. 不同偏离角的局部放电点设置
3.4. 仿真结果
首先对高压绕组匝间局部放电进行仿真,MUSIC-SRP算法对变压器高压上层绕组匝间局部放电定位结果如表2所示。

Table 2. Positioning results of MUSIC-SRP algorithm for high voltage upper winding
表2. 高压上层绕组MUSIC-SRP算法定位结果
MUSIC-SRP算法对变压器高压中层绕组匝间局部放电定位结果如表3所示。

Table 3. Location results of MUSIC-SRP algorithm for high voltage middle winding
表3. 高压中层绕组MUSIC-SRP算法定位结果
MUSIC-SRP算法对变压器高压下层绕组匝间局部放电定位结果如表4所示。

Table 4. Positioning results of MUSIC-SRP algorithm for lower winding of high voltage
表4. 高压下层绕组MUSIC-SRP算法定位结果
然后对低压绕组匝间局部放电进行仿真,MUSIC-SRP算法对变压器低压上层绕组匝间局部放电定位结果如表5所示。

Table 5. Location results of MUSIC-SRP algorithm for low voltage upper winding
表5. 低压上层绕组MUSIC-SRP算法定位结果
MUSIC-SRP算法对变压器低压中层绕组匝间局部放电定位结果如表6所示。

Table 6. Location results of MUSIC-SRP algorithm for low voltage middle winding
表6. 低压中层绕组MUSIC-SRP算法定位结果
MUSIC-SRP算法对变压器低压下层绕组匝间局部放电定位结果如表7所示。

Table 7. Location results of MUSIC-SRP algorithm for low voltage lower winding
表7. 低压下层绕组MUSIC-SRP算法定位结果
以仿真实验中局部放电发生在高压中层绕组偏离角为15˚时,局放坐标为(5.4, 40.0, −4.3),波达方向 (82.3, 96.1),MUSIC测向结果为(87.7, 92.5),根据上述原理MUSIC测向后确定的搜索范围为:z的搜索范围为[−9, 0] cm;x的搜索范围为[0, 17.7] cm;y的搜索范围为[32.4, 114.5] cm,大于由于绕组高度与传感器阵列到绕组距离之和70 cm,故调整调整后y的搜索范围为[32.4, 70]cm。可得SRP搜索空间上限为[17.7, 70, 0];下限为[0, 32.4, −9]。而MUSIC测向压缩空间前搜索空间为上限为[17.7, 70, 6];下限为[−17.7, 10, −9],约为压缩后搜索空间的5.3倍。
通过仿真结果可以看出对35 kV变压器单相绕组内部局部放电定位精度均在10 cm以内,较SRP算法定位精度有极大提升。主要是由于MUSIC测向后对SRP搜索空间进行压缩,最终的搜索空间缩小四至五倍,使定位精度提升。MUSIC-SRP定位算法对变压器高低压绕组匝间放电定位适用性良好。偏离角越大,定位误差越大,这是由于本文所用的十字型传感器阵列俯仰角和方向角越偏离90˚,测向误差越大。纵向深度越深,定位误差越大,这是由于超声波传播路径长会有少许信号衰减,影响波形幅值,进而影响定位精度。匝间深度不同,对定位精度影响不大,由于匝间深度差别仅在1、2 cm,对超声波传播影响较,小可忽略不计。MUSIC-SRP算法定位得到的结果依旧存在少许误差,其来源于以下几个方面:
1) 由于不用阵列形状对某一方向上的测向有不同的误差。因此在放电源对传感器阵列不同角度情况下,产生了不同误差;
2) 由于考虑MUSIC算法测向结果的误差,可能将SRP搜寻范围并没有缩小到最小,产生误差;
3) 由于变压器内部结构复杂,局部放电超声信号传播过程中会发生反射、散射等现象。传感器接收到的超声信号中包含混响信号,这会对局部放电定位产生影响。
4. 实验研究
4.1. 实验平台建立
建立油中局部放电测向实验平台,包括模拟变压器油箱、变压器绕组模型和局部放电模型。模拟变压器油箱尺寸为200 cm × 100 cm × 150 cm,里面充满25#变压器油,油箱外壳接地。绕组模型为35 kV变压器绕组,其高度0.6 m,高压绕组外径0.24 m、内径0.2 m,低压绕组外径0.13 m、内径0.1 m,绕组铁芯高度为0.6 m、半径为0.1 m,如图12所示。实验选取尖端放电模型,即采用了针板电极模型,如图13所示。其高压电极采用一黄铜尖棒,高压电极与地电极之间间距可根据需要放电量的多少进行调节。为了研究MUSIC-SRP算法估计局部放电位置,设计了超声波采集系统,实验系统如图14所示。

Figure 14. Optical fiber sensor test platform of partial discharge
图14. 局部放电光纤传感器检测实验平台
4.2. 结合算法局部放电定位实验
实验环境与仿真设置类似,传感器阵列放置位置也与仿真情况类似,设置在变压器绕组上方正对这一侧油道处。但由于实际环境限制,传感器阵列只能高于绕组5 cm。分别在高低压绕组匝间的不同匝间深度、不同纵向深度和不同偏离角度上选择多个特征点设置局部放电点,先后进行实验。
首先进行高压绕组匝间进行局部放电实验,局部放电源设置在变压器高压绕组内侧,如图15所示。高压绕组匝间所选局部放电点相对位置如图16。

Figure 15. Placement of partial discharge power supply in high voltage winding
图15. 局部放电源在高压绕组的放置方式
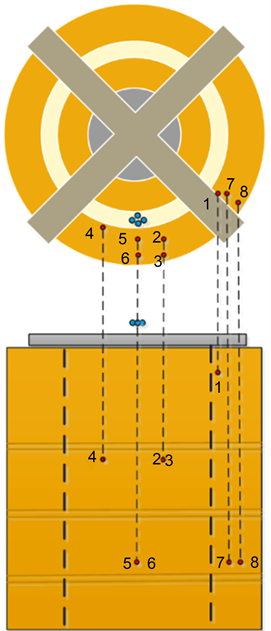
Figure 16. Relative position of partial discharge point between turns of high voltage winding
图16. 高压绕组匝间局部放电点相对位置
MUSIC-SRP算法对变压器高压绕组匝间局部放电定位实验结果如表8所示。

Table 8. Experimental results of MUSIC-SRP algorithm location for high voltage winding
表8. 高压绕组MUSIC-SRP算法定位实验结果
之后进行低压绕组匝间进行局部放电实验,局部放电源设置在变压器低压绕组外侧,如图17所示。低压绕组匝间所选局部放电点相对位置如图18。

Figure 17. Placement of partial discharge power supply in low voltage winding
图17. 局部放电源在低压绕组的放置方式
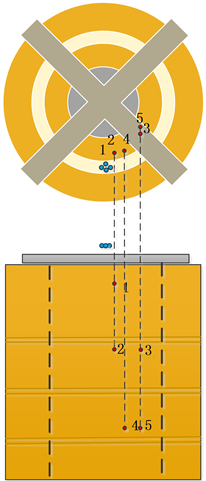
Figure 18. Relative position of partial discharge point between turns of low voltage winding
图18. 低压绕组匝间局部放电点相对位置
MUSIC-SRP算法对变压器低压绕组匝间局部放电定位结果如表9所示。

Table 9. Positioning results of MUSIC-SRP algorithm for low voltage winding
表9. 低压绕组MUSIC-SRP算法定位结果
可以看出,实验结果误差在可接受范围内,证明MUSIC-SRP算法可以用于变压器高低压绕组匝间局部放电定位中。实验结果与仿真结果比较可以发现误差规律近似。偏离角越大,定位误差越大;纵向深度越深,定位误差越大;匝间深度不同,对定位精度影响不大。实验误差比仿真误差略大,除了分析过的阵列形状带来的误差、MUSIC算法测向误差和混响误差,还有一下几方面的误差来源:
1) 实验环境中存在一些少量的外部噪声,会对对局部放电超声信号波形产生改变,会对定位结果带来些微小误差;
2) 实验中所用的四个光纤FP传感器中心频率需要统一在30 kHz,但实际中四个传感器的中心频率可能会有微小偏差,造成定位误差;
3) 实验过程中的局部放电点坐标都是人为量测设置的,存在量测误差。
5. 结论
对传统定位算法MUSIC算法和SRP算法应用于变压器高低压绕组匝间局部放电定位的优缺点进行了分析,从而提出了MUSIC-SRP结合算法。详细介绍了利用MUSIC测向估计将SRP搜索空间有效压缩这一核心步骤。通过算例可以看出经过MUSIC测向估计可将SRP搜索空间压缩至原来的五分之一,从而达到提升定位精度的目的。
仿真和实验结果表明,MUSIC-SRP结合算法定位精度较SRP算法有极大提升,相较于所用实验模型尺寸,定位误差在可接受范围之内,适用于变压器绕组内部局部放电的定位。