摘要:
设{Xn}n=1∞ 是一列任意相依随机变量序列,且{Xn}n=1∞ ≺ X。本文利用Borel-Cantelli引理与概率论极限理论中的纯分析方法,讨论一类相依随机变量序列的强收敛性,得到了任意相依随机变量序列加权和的强大数定律普遍成立的若干充分条件,并推广了已有的结果。
Abstract:
Let {Xn}n=1∞ be a sequence of arbitrarily dependent random variables with {Xn}n=1∞ ≺ X. In this paper, by using the Borel-Cantelli lemma and the pure analysis method in probability limit theory, some strong convergence of a class of dependent random variables is discussed and some sufficient conditions on strong law of large numbers for weighted sums of arbitrarily random sequences are also obtained. Some classical results are generalized.
1. 引言
关于独立随机序列的极限理论曾是概率论极限理论研究的中心课题,并取得了十分丰富的成果,其系统的结果总结在文献[1] [2] 等专著中,对任意相依随机序列的极限行为的研究也是有许多有意义的结果。文献 [3] 利用矩估计的方法研究了同分布任意相依随机变量序列的强大数定律,文献 [4] 研究任意随机序列的强收敛性,作为推论,得到了一类鞅差序列的强大数定律,一类随机序列公平比的强极限定律以及任意随机序列部分和估计定理,文献 [5] 利用区间剖分法构造几乎处处收敛的鞅,得到了一个对任意M-值随机变量序列普遍成立的强极限定理,作为推论得到一个精细的Borel-Cantelli引理,文献 [6] 在对随机变量没有任何独立性假设的条件下,讨论了随机序列的强大数定律,文献 [7] [8] 将一般随机变量序列的强大数定律的研究推广到任意B值空间上来研究。本文中我们利用随机受控的概念,结合经典的Borel-Cantelli引理与概率论极限理论中的纯分析方法,讨论一类相依随机变量序列的强收敛性,给出了任意随机变量序列加权和的强大数定律普遍成立的若干充分条件,将文献[9] 中的结果推广到一般的随机变量序列中。
本文中 表示常数,它在不同的表达式中可表示不同的值。
表示常数,它在不同的表达式中可表示不同的值。
2. 预备知识
定义2.1 [10] 称随机变量序列 被随机变量
被随机变量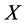 控制,若存在一个常数
控制,若存在一个常数 ,有
,有

简记为 。
。
引理2.1 [10]  与
与 都是随机变量,且
都是随机变量,且 。即
。即
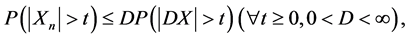
则对 ,有
,有

其中IA表示A的示性函数。
3. 主要结论与证明
定理3.1 设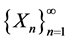 是随机变量序列,且
是随机变量序列,且 ,
, 是两个常数序列,满足
是两个常数序列,满足 ,
, ,
,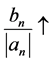 ,并且
,并且
 (1)
(1)
和
 (2)
(2)
则
 (3)
(3)
和
 , a.s. (4)
, a.s. (4)
证明 令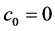 ,
, ,
, (文中所遇
(文中所遇 均如此定义)。由定义2.1及引理2.1,知
均如此定义)。由定义2.1及引理2.1,知
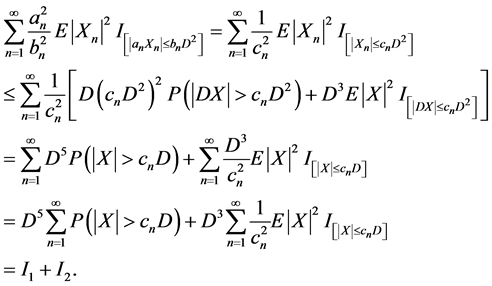
由(2)知I1式有限,往证I2式有限。注意到

由(1)得上述不等式右边

即得I2式有限,由此
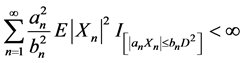 .
.
往证(4)成立。令
 ,
,
由(3)知
 ,
,
因此
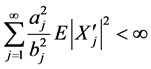 , a.s.
, a.s.
由Kroncher引理有
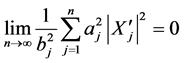 , a.s.
, a.s.
由 不等式有
不等式有
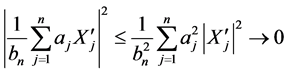 ,
,
则有
 , a.s.
, a.s.
于是
 , a.s.
, a.s.
定理3.2 设 是随机变量序列,且
是随机变量序列,且 。
。 是两个常数序列,满足
是两个常数序列,满足 ,
,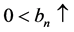 ,
, ,且
,且
 ,
,  , (5)
, (5)
若(2)成立,则
 , a.s.
, a.s.
证明 由
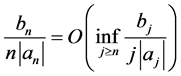
可知

又

由定理3.1知
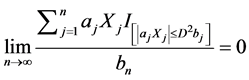 , a.s.
, a.s.
所以若有
 , a.s. (6)
, a.s. (6)
则有
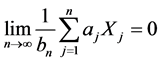 , a.s.
, a.s.
往证(6)成立

由B-C引理知
 ,
,
从而(6)成立,故
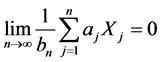 , a.s.
, a.s.
定理3.3 设 是随机变量序列,且
是随机变量序列,且 。
。 是两个常数序列,满足
是两个常数序列,满足 ,
,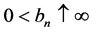 ,
, ,并且
,并且
 ,
,  ,
,
如果
 , (7)
, (7)
成立,则
 , a.s.
, a.s.
证明 因为
 ,
,
由定理3.2易知只需证
 ,
,
令 ,易知
,易知 且有
且有
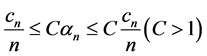 . (8)
. (8)
令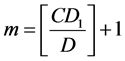 ,由(8)得
,由(8)得

则

由(7)知
 ,
,
所以
 , a.s.
, a.s.
基金项目
安徽工业大学青年教师科研基金(QZ201314);安徽省自然科学基金(1408085MA04);安徽工业大学研究生创新基金资助(2015126)。
*通讯作者。