1. 引言
在化学图论中,我们用一个图来描述分子的拓扑结构,用顶点表示原子,边表示化学键,该图称为分子图。拓扑指数是从化合物的结构图衍生出来的不变量。它不但可以定量的描述分子的结构,而且可以分析相关分子的结构与性能之间的关系。相关内容可参考 [1] - [12] 。
用 表示顶点/原子
表示顶点/原子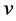 的度。分子图
的度。分子图 的拓扑指数是分子结构数值化的一种方式。1972年Trinajstić和Gutman引入了的第一Zagreb指数和第二Zagreb指数:
的拓扑指数是分子结构数值化的一种方式。1972年Trinajstić和Gutman引入了的第一Zagreb指数和第二Zagreb指数:
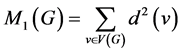 ,
,
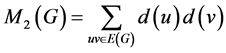 。
。
1975年,美国化学家Milan Randić [2] 提出了最古老的连通性指数,定义为
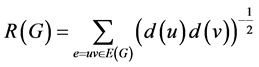
1988年,Bollobas和Erdos在 [6] 中推广了Randi指数,用任意实数k代替了,从而定义了广义的Randić指数:
 ,
,
其中k是非零实数。以下若没有特别说,k均表示非零实数。
当k = 1时,广义的Randić指数就是我们通常说的第二Zagreb指数。当k = −1时,广义的Randić指数就是修改的第二Zagreb指数。
Azari和Iranmanesh [13] 引入广义Zagreb指数,定义为
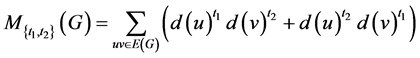 ,
,
其中 和
和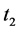 为任意的非负整数。
为任意的非负整数。
和连通指数则定义为:
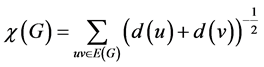
推广形式的和连通指数为
 。
。
而调和指数则定义为:
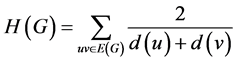
它的广义形式为:
 。
。
Eliasi和Iranmanesh [14] 定义广义几何代数指数如下:
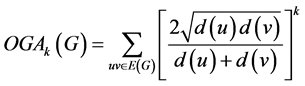 。
。
当k = 1时,即为一般GA指数如下:
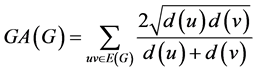 。
。
Estrada等人 [15] 定义原子键连通指数(atom-bound connectivity index,简称ABC指数)如下:
 。
。
两类Zagreb指数对应的多项式分别为
 ,
,
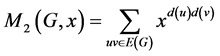 。
。
此外,第三类Zagreb指数和多项式定义为
 ,
,
 。
。
Gutman [16] 给出分子图的乘法Zagreb指数定义如下
 ,
,
 。
。
其中 为第一类乘法Zagreb指数,
为第一类乘法Zagreb指数, 为第二类乘法Zagreb指数。
为第二类乘法Zagreb指数。
Usha等人 [17] 重新定义了三类Zagreb指数如下:
 ,
,
 ,
,
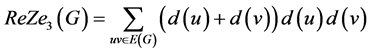 。
。
Furtula和Gutman [18] 定义了F指数如下:
 。
。
设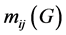 为满足
为满足 和
和 的边e = uv的个数,则M-多项式定义为
的边e = uv的个数,则M-多项式定义为
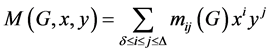 。
。
广义ABC指数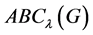 和and增强的Zagreb指数
和and增强的Zagreb指数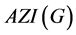 则定义为 [19] :
则定义为 [19] :
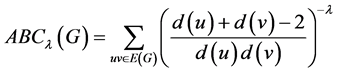 ,
,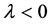
 。
。
最后,减弱的倒数Randić指数定义为
 。
。
第二减弱的倒数Randić指数定义为
 。
。
Pent-Heptagonal纳米管 是由周期长度为5的
是由周期长度为5的 (五边形)和周期长度为7的
(五边形)和周期长度为7的 (七边形)相互交替构成的网状化合物。设
(七边形)相互交替构成的网状化合物。设 纳米管的2维拉丁网格中,第一行和列的7边形个数分别为m和n (见图2)。将
纳米管的2维拉丁网格中,第一行和列的7边形个数分别为m和n (见图2)。将 纳米管记为
纳米管记为 。
。 纳米管的圆柱和2维拉丁网络可参考图1和图2。
纳米管的圆柱和2维拉丁网络可参考图1和图2。

Figure 1. Pent-Heptagonal Nanotubes cylindrical lattice
图1. Pent-Heptagonal纳米管的圆筒晶格
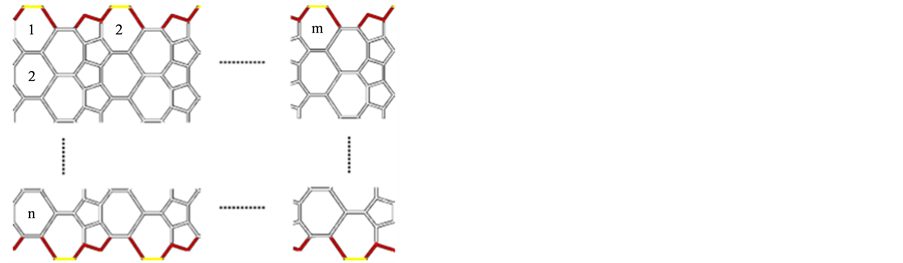
Figure 2. Pent-Heptagonal two-dimensional lattice of nanotubes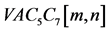
图2. Pent-Heptagonal纳米管的二维晶格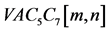
本文利用边集合划分方法得到Pent-Heptagonal纳米管若干基于度的拓扑指数计算公式。
2. 主要结果
将Pent-Heptagonal纳米管的顶点集和边集合作如下划分:
 ,
,
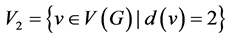 ,
,
 ,
,
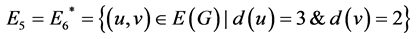 ,
,
 。
。
从图2来看,在Pent-Heptagonal纳米管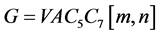 中分别用m和n来表示第一行和第一列的七边形数量,则有纳米管的顶点数
中分别用m和n来表示第一行和第一列的七边形数量,则有纳米管的顶点数 ,并且有:
,并且有:
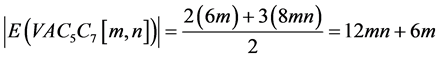
并且,我们在图2中用黄色标记 、
、 的边,用红色标记
的边,用红色标记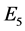 、
、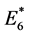 的边,
的边, 用白色标记。因此,得到
用白色标记。因此,得到 的大小等于
的大小等于 ,
,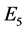 的大小为
的大小为 。换句话说,以上边的数量划分为
。换句话说,以上边的数量划分为 和
和 ,我们有以下的表格:
,我们有以下的表格:
于是,利用上表以及各种拓扑指数的定义,我们得到:
广义的Randić指数为:
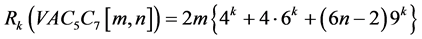
修改的第二Zagreb指数为:
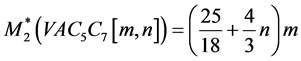
广义Zagreb指数为:
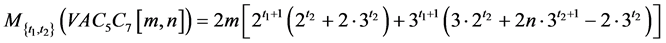
和连通指数为:
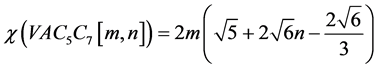
推广形式的和连通指数为:
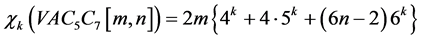
调和指数为:
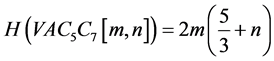
调和指数的广义形式为:
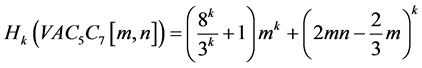
广义几何代数指数为:
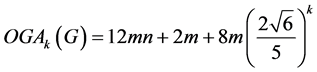 。
。
一般GA指数为:
 。
。
原子键连通指数为:
 。
。
两类Zagreb多项式分别为
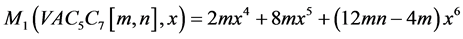 ,
,
 。
。
第三类Zagreb指数和多项式分别为:
 ,
,
 。
。
两类乘法Zagreb指数分别为:
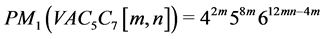
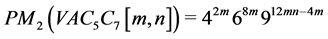 。
。
重新定义的三类Zagreb指数分别为:
 ,
,
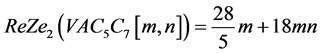 ,
,
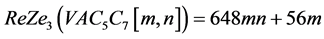 。
。
F指数为:
 。
。
M-多项式为
 。
。
广义ABC指数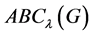 和and增强的Zagreb指数
和and增强的Zagreb指数 分别为:
分别为:
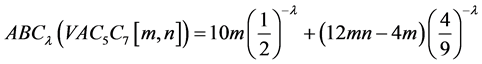 ,
,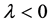
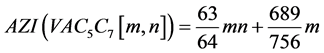 。
。
两类减弱的倒数Randić指数分别为
 。
。
第二减弱的倒数Randić指数定义为
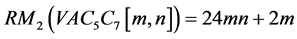 。
。
3. 总结
随着化学实验条件的改善和新化学生物技术的发现及应用,每年有大量复杂的化学分子被发现。在化学领域,化学家们会通过大量实验,来研究新物质的性质,比如:熔点、沸点、毒性、氧化性等等。因而对每年发现的大量新物质的研究需要大量仪器设备和药品试剂,造成了研究的高成本。但是,如果把化学分子的结构用图模型来表示的话,化学分子的特性就可以用一些参数来衡量,比如Zagreb指数、维纳指数、Randić指数等。本文利用边集合划分方法得到的Pent-Heptagonal纳米管若干基于度的拓扑指数计算公式,计算结果可运用到新化学分子的性质研究上,进而可以大大节约研究成本以及研究时间。