1. 引言
在工程处理的各个领域中,越来越多的学者开始从事分数阶偏微分方程的研究,并且成果显著。近几年在数学物理中出现了非线性分数阶微分方程的研究,引起了人们极大的关注。尤其是KdV-ZK类型 [1] [2] 的方程,由于其沿水表面的行波性质和其在固体物理、等离子体物理和量子场论中的各种应用,对KdV-ZK方程的研究变得越来越重要。与常微分方程相比,分数阶微分方程可以推广到任意(非整数)阶。由于其在工程和科学上的显著应用,分数阶微分方程逐渐成为当前的研究热点。
在本文中,我们主要研究KdV-ZK方程的近似解析解问题。数学物理中KdV-ZK方程可以用来描述耦合非线性传输线中的非线性波与水波在空间中的运动规律, Zakharov和Kuznetsov在研究过程中首次推导出该方程,且以他们的名字命名 [3] [4] [5] [6] 。由于大部分的KdV-ZK方程的精确解不容易求解出来,目前求解方程的数值解及近似解析解算法已成为一个重要的任务,所以学者通常采用解析和数值方法对方程进行研究。目前已经有很多求解分数阶微分方程的方法并应用到KdV-ZK方程的求解中 [7] [8] [9] [10] [11] 。文献 [12] 中提出的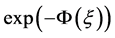 方法为求解分数阶微分方程的近似解析解提供了解决方案,此方法利用齐次平衡原理 [13] 进行处理。
方法为求解分数阶微分方程的近似解析解提供了解决方案,此方法利用齐次平衡原理 [13] 进行处理。
近似解析解的获得有助于我们更好地了解此方程所表现出的物理现象。借助分数阶导数的复变换,非线性时间分数阶微分方程可转化为整数阶的常微分方程。最近,一些强大的方法已被提出。例如,(G'/G)-expansion方法 [14] 。
本文的目的是使用 方法求解KdV-ZK方程的近似解析解。行文安排如下:在第2节中,给出了本文将要使用的分数微积分的一些定义。在第3节中,给出了方法的说明和具体计算步骤。在4节中我们用此方法求解时间分数阶微分方程的具体算例。在第5节中给出文章的结论。
方法求解KdV-ZK方程的近似解析解。行文安排如下:在第2节中,给出了本文将要使用的分数微积分的一些定义。在第3节中,给出了方法的说明和具体计算步骤。在4节中我们用此方法求解时间分数阶微分方程的具体算例。在第5节中给出文章的结论。
2. 准备工作
本节我们主要介绍一些文章中将用到的关于分数阶微积分的一些预备知识。具体请参考文献 [15] [16] [17] [18] 。
定义 2.1 假设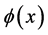 是定义在包含
是定义在包含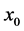 和
和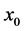 领域内的所有点的区间上的函数,如果对于任意的正常数
领域内的所有点的区间上的函数,如果对于任意的正常数 ,存在正常数
,存在正常数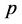 、
、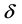 ,当
,当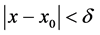 时,有
时,有
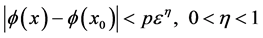 , (1)
, (1)
则称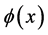 在
在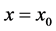 处局部分数连续,即满足
处局部分数连续,即满足
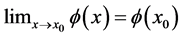 ,
,
因此,如果
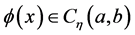 ,(2)
,(2)
其中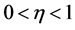 是分形维数,则称函数
是分形维数,则称函数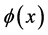 在区间
在区间 上局部分数阶连续。
上局部分数阶连续。
定义2.2 函数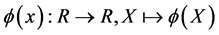 是指数为
是指数为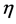 的不可微函数,并关于指数
的不可微函数,并关于指数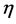 满足Hölder方程,则当
满足Hölder方程,则当 时,我们有
时,我们有
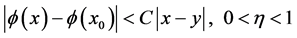 . (3)
. (3)
定义2.3 如果函数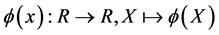 满足
满足
 , (4)
, (4)
则称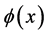 是关于指数
是关于指数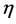 局部分数阶连续的。
局部分数阶连续的。
注:函数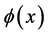 在空间
在空间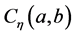 中,当且仅当对任意的
中,当且仅当对任意的 ,
,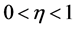 ,满足
,满足
 .
.
定义2.4 假设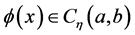 ,则
,则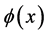 在
在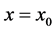 处的
处的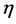 阶局部分数导数定义如下:
阶局部分数导数定义如下:
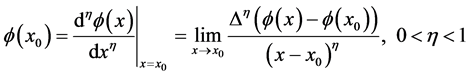 , (5)
, (5)
其中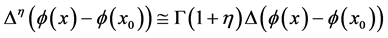 。
。
注:如果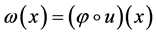 ,则当
,则当 时,存在
时,存在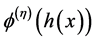 ,
,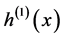 和
和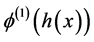 ,
,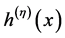 使得
使得
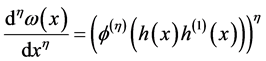 , (6)
, (6)
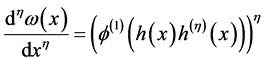 . (7)
. (7)
在 方法中,等式(7)在分数阶的变换中起到至关重要的作用。
方法中,等式(7)在分数阶的变换中起到至关重要的作用。
注:
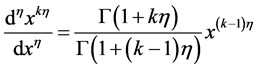 ,
,
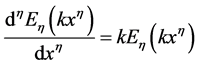 ,
,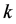 为常数。
为常数。
这些导数在研究高度不规则和不可微函数的分数阶可微性方面发挥着重要的作用。
3. Exp(-Φ(ξ))方法的基本思想
本节我们考虑非线性分数阶微分方程的一般形式:
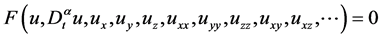 , (8)
, (8)
其中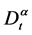 是在关与
是在关与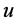 关于
关于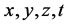 的局部分数导数,
的局部分数导数, 是
是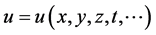 和
和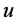 的各阶导数的多项式,其中包含非线性项和
的各阶导数的多项式,其中包含非线性项和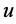 的最高阶导数。寻求分数阶微分方程的近似解析解的主要步骤如下 [19] :
的最高阶导数。寻求分数阶微分方程的近似解析解的主要步骤如下 [19] :
步骤1:考虑下面的非线性分数阶复变换,使用分数阶变量变换 [20] [21] [22] [23] :
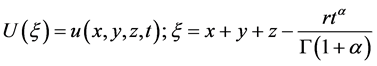 , (9)
, (9)
其中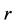 是一个任意的非零常数,通过在(7)中使用链式规则,我们可以得到
是一个任意的非零常数,通过在(7)中使用链式规则,我们可以得到
 ,
,
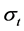 称为分形指标,我们通常令
称为分形指标,我们通常令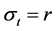 ,其中
,其中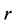 是一个常数。
是一个常数。
利用方程式(9)将程式(8)转化为下面的非线性常微分方程
 , (10)
, (10)
其中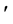 表示
表示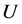 于
于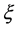 的导数。下面我们对方程式(10)进行逐项积分。
的导数。下面我们对方程式(10)进行逐项积分。
步骤2:根据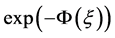 的方法,方程(10)的近似解析解可以用以下的形式表示:
的方法,方程(10)的近似解析解可以用以下的形式表示:
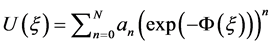 , (11)
, (11)
这里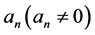 是待定常数,
是待定常数,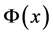 满足下列辅助常微分方程:
满足下列辅助常微分方程:
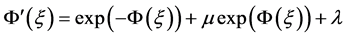 , (12)
, (12)
因此辅助方程式(12)有如下不同形式的解:
① 当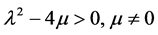 时,
时,
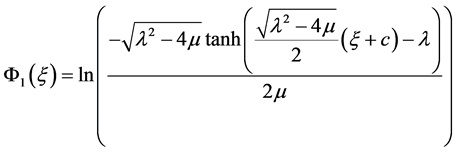 , (13)
, (13)
② 当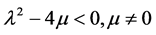 时,
时,
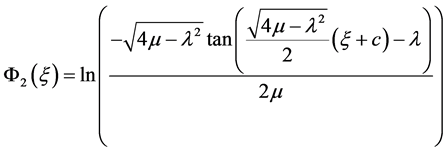 , (14)
, (14)
③ 当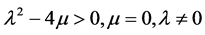 时,
时,
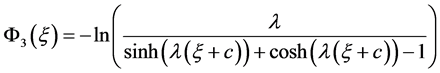 , (15)
, (15)
④ 当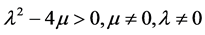 时,
时,
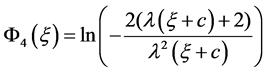 , (16)
, (16)
⑤ 当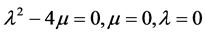 时,
时,
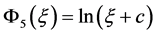 , (17)
, (17)
其中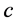 是积分常数。其中平衡数
是积分常数。其中平衡数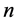 是通过最高阶线性项和不等式(11)的最高阶非线性项的平衡确定的。
是通过最高阶线性项和不等式(11)的最高阶非线性项的平衡确定的。
步骤3:将方程(11)带到方程(10)中,把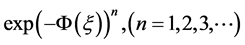 相同项的系数加在一起从而得到一个多项式,然后令这些多项式等于0产生一个代数方程组,通过求解方程组构造方程(8)的近似解析解。
相同项的系数加在一起从而得到一个多项式,然后令这些多项式等于0产生一个代数方程组,通过求解方程组构造方程(8)的近似解析解。
4. 数值算例
本节我们考虑KdV-ZK方程
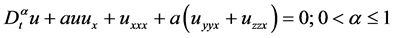 (18)
(18)
的解,其中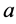 是任意常数,为了得到最终结果,给出了以下变换:
是任意常数,为了得到最终结果,给出了以下变换:
 , (19)
, (19)
其中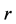 是非零常数。变换后积分方程只有
是非零常数。变换后积分方程只有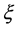 一个变量,将方程(19)代入方程(18),得到如下常微分方程:
一个变量,将方程(19)代入方程(18),得到如下常微分方程:
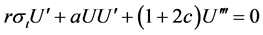 ,
,
其中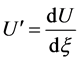 。对上式两边逐项进行积分,我们得到
。对上式两边逐项进行积分,我们得到
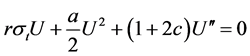 , (20)
, (20)
其中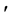 表示
表示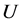 对
对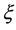 的导数,通过最高阶导数项
的导数,通过最高阶导数项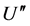 和方程(20)的非线性项
和方程(20)的非线性项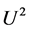 的平衡,我们得到平衡数
的平衡,我们得到平衡数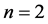 。所以有:
。所以有:
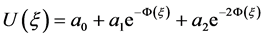 . (21)
. (21)
将(21)式代入到(20)式,然后把 的相同项的系数加在一起从而得到一个多项式,再令这些多项式等于0得到如下代数方程组:
的相同项的系数加在一起从而得到一个多项式,再令这些多项式等于0得到如下代数方程组:
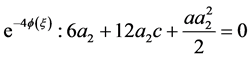 ;
;
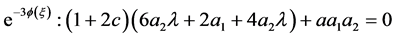 ;
;
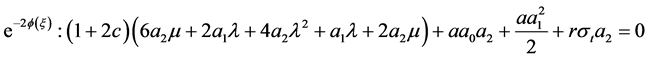 ;(22)
;(22)
 ;
;
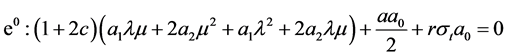 ;
;
然后用Maple分组程序求解上述代数方程组,得到如下两个结果:
结果1:
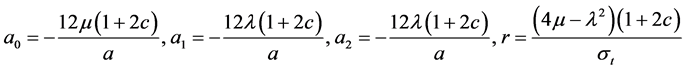 , (23)
, (23)
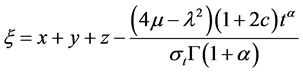 , (24)
, (24)
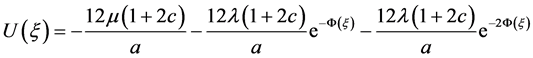 . (25)
. (25)
对此结果我们有以下不同情况的KdV-ZK方程的精确解:
a) 当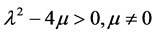 时,
时,
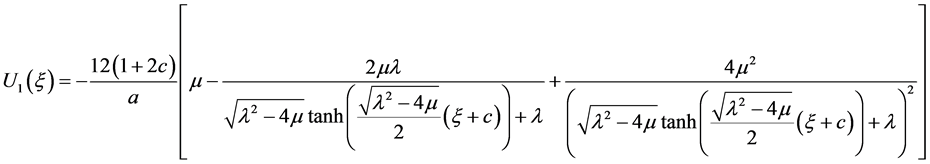 .
.
b) 当 时,
时,
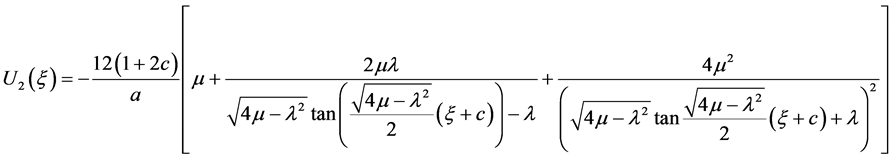 .
.
c) 当 时,
时,
 .
.
d) 当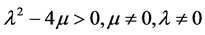 时,
时,
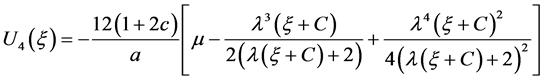 .
.
e) 当 时,
时,
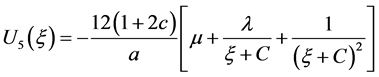 .
.
结果2:
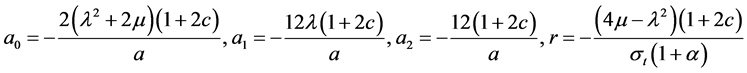 , (26)
, (26)
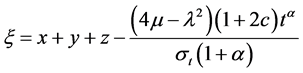 , (27)
, (27)
 , (28)
, (28)
对此结果我们有以下不同情况的KdV-ZK方程方程的精确解:
a) 当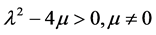 时,
时,
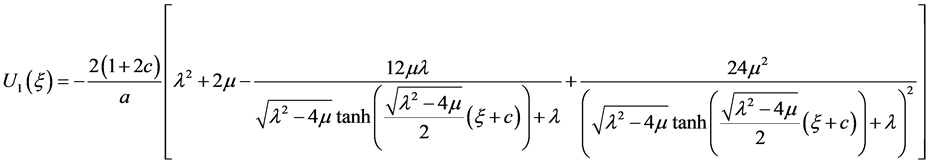 .
.
b) 当 时,
时,
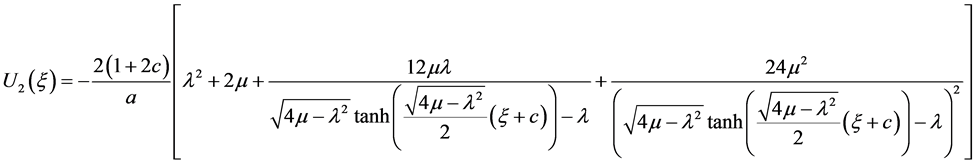 .
.
c) 当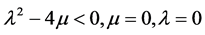 时
时
 .
.
d) 当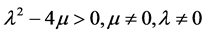 时
时
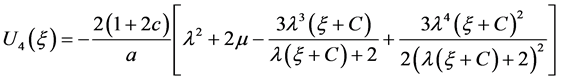 .
.
e) 当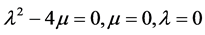 时
时
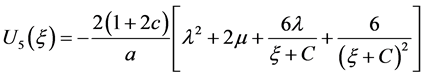 .
.
5. 总结
本文研究的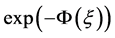 方法是为了解决(3+1)维时间分数阶KdV-ZK方程。分析得到了方程在不同情况下的近似解析解。数值算例表明该算法是非常有效的。由于上述方法是基于齐次平衡原理,它也可以扩展到其他分数阶偏微分方程和方程组,为齐次平衡原理提供近似解析解的解决方案。
方法是为了解决(3+1)维时间分数阶KdV-ZK方程。分析得到了方程在不同情况下的近似解析解。数值算例表明该算法是非常有效的。由于上述方法是基于齐次平衡原理,它也可以扩展到其他分数阶偏微分方程和方程组,为齐次平衡原理提供近似解析解的解决方案。
基金项目
新疆维吾尔自治区杰出青年科技人才培养项目(No.QN2016JQ0367),国家自然科学基金项目(No.11461072),新疆师范大学数学校级重点学科。