1. 引言
2007年,美国爆发次贷危机,多家大型的投资银行及其他金融机构相继倒闭,致使全球主要金融市场出现流动性危机,给全球的银行系统和金融系统造成了巨大的冲击,最终引发了一场全球性金融危机。此次金融危机表现出了全球一体化后银行系统的脆弱性和关联性。银行间日趋紧密的联系似乎有助于降低金融危机爆发的可能性,然而一旦发生了,这个危机就会演变成全球性的危机。因此,研究银行系统性风险已成为国内外学术界和政府监管机构关注的焦点。这一研究无疑对防范和化解系统性风险、维护金融稳定具有重要意义。
同业拆借业务不仅能够帮助银行缓解流动性不足,也是商业银行获取较低成本资金的主要途径,是利率市场化条件下商业银行应对存款压力、息差收窄压力、拓展经营收益的一种重要方式。但是,由同业拆借业务所构成的复杂的银行间拆借网络是违约传染的主要渠道之一,因此利用网络模型研究银行系统性风险是近期的一个研究热点 [1] 。
2000年,Allen和Gale [2] ,Freixas [3] 等人的研究最早提出:银行系统的稳定性与银行间拆借网络结构有关。此后,学者们对不同国家的银行间拆借网络进行实证研究,发现真实的银行拆借网络与其他领域的网络如国家电网、社区网络等同样具有复杂网络的结构特征。他们利用银行间风险暴露的相关数据,发现银行网络结构具有小世界、无标度等复杂网络结构特征 [4] [5] [6] [7] [8] 。并且国内外均有学者通过仿真或实证的方式分析了无标度网络对银行间市场的影响 [9] - [14] 。然而,许多无标度网络中主张的统计学理论依据受到了质疑 [15] ,其原因应归结为无标度网络的渐进性。无标度网络中,即使在数据集很大的情况下也只能观测到极少量的极端度值。现实中,银行系统内的节点往往都是有限的并且规模是固定的,所以把银行系统构建成无标度网络(持续增长)并不合适 [16] 。Craig和von Peter [7] 认为银行间拆借市场是有层次的,大多数的银行不是直接发生借贷而是通过货币中心银行作为中介,因此建立“货币中心系统”模型更为合适。Craig和von Peter建立的核心边缘模型首次将“货币中心银行”等概念进行了定量的描述,研究发现德国的银行网络中核心银行占2.7%。随后,in’t Veld和van Lelyveld [16] 同样发现核心边缘网络模型能最好地描绘荷兰银行同业市场的网络结构。
目前,还未有文献对核心边缘网络与其他网络对银行系统的稳定性影响的进行比较研究。因此本文首先构建核心边缘网络模型,并构造网络的拆借矩阵,在此基础上构建了动态的银行演化系统,通过仿真计算比较了核心边缘网络模型与随机网络模型在面临存款波动后(分别讨论了边缘银行、核心银行受到冲击的情况)银行系统的稳定性,为监管部门的决策提供参考。
2. 模型
2.1. 核心边缘网络结构构建
假定银行网络系统中所有银行组成的集合为
,其中集合
包含全部的核心银行(通常为资产规模较大的银行),集合
包含全部的边缘银行(通常为资产规模相对较小的银行),并且满足全部核心银行的总资产不少于全部边缘银行的总资产这一条件。
首先,本文用邻接矩阵
来表示银行间是否存在拆借关系。
表示银行i和银行j之间存在拆借关系,
表示i和j不存在拆借关系。
表示银行系统的连接度,
表示系统内不存在银行间的拆借市场,
表示系统内任意两个银行之间都存在拆借关系。核心边缘网络的拓扑结构需要满足以下三个条件 [16] :
a) 核心银行之间全连接
;
b) 边缘银行之间无连接
;
c) 核心银行至少与边缘银行存在一借一贷的连接(随机连接,连接个数取决于银行系统的连接度)
.
一般来说借贷关系是相互的,因此本模型的邻接矩阵是对称的,
,即i能借给j,j也能借给i。此外,银行不能与自身发生借贷关系,所以规定
。因此银行间拆借关系的邻接矩阵
可以表示为:
(1)
其中,
对角线元素为0,非对角线元素为1 (条件a);
每一行至少有一个1 (条件c);
是
的转置;
为0向量(条件b)。
通过上述银行系统的连接度的
和银行间邻接矩阵
,及边缘和核心银行的参数设置,即可得出银行间的拆借矩阵
,其中
表示银行i拆出给银行j的资金,
表示i银行的总拆出资金,
示j银行的总拆入资金。
2.2. 动态银行网络系统模型
基于2.1节构建的银行间拆借网络,本节将结合银行间的资产负债关系,构建动态银行网络系统模型。
表1是本文假设的简易银行资产负债表,涉及的科目都与本模型直接相关。根据表1,可得恒等式(4):
表1. 银行的资产负债表
(2)
(3)
由于网络中的银行随时间动态演化,每个演化时间t,每个银行的资产负债表均包括期初,期中,期末三个状态 [17] 。
期初:
(4)
期中:
(5)
(6)
期末:
(7)
(8)
(9)
(10)
模型中
表示投资期,
表示第
家银行,
是存款利率,
是拆借利率,
是投资收益率,
投资机会,
是存款波动,
是投资机会波动,
是分红金额,
是央行规定的存款准备金率,
是银行规定的所有者权益占存款比例的下限,
表示系统动态演化的时间步。模型中各参数的初始值
是外生的,除拆借矩阵初始值
是通过上节中估算矩阵
的模型得到的,其他参数均是资产负债表中的数据值。同时拆借网络是建立在一定的拆借规则上的,利用图1来说明本模型中网络节点之间的拆借规则。与i直接连接的银行,记为集合
(内圈);与i间接连接的银行,记为集合
(外圈) (见图1(a))。模型规定,当期中
且没有途径拆入资金时,或者期末
时,即流动性资金不足时,银行破产。银行存款受到冲击是一种影响银行系统稳定性的情况,本文将围绕这种情景对比两种网络结构下银行系统的稳定性,通过公式(11)中衡量冲击强度的参数p实现对存款的冲击。在整个银行系统模型运行完给定的仿真时间后,以系统内存活的银行数量作为衡量系统稳定性的基本标准之一,系统中存活的银行数量越多,系统越稳定(见图1(b))。
(11)
3. 仿真与结论
本章通过Matlab实现动态银行网络系统模型的仿真计算,比较核心边缘网络与随机网络在面对存款
冲击时的稳定性。面对存款的冲击时,对于核心边缘网络的银行系统,分为两种情况的冲击,即边缘银行受到冲击及核心银行受到冲击,而对于随机网络而言,所有银行均随机连接,存款冲击的银行也都是随机产生的,无核心银行与边缘银行的区别。
3.1. 核心边缘网络结构估算
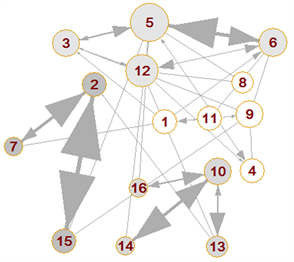
本文根据2.1构造一个银行网络系统,假设该银行网络系统有16家银行,在连接度C = 0.45的条件下,构建结果如图2(a)所示(这里采用核心银行个数为4的情况来举例);同时,为了对比核心边缘网络与随机网络银行系统稳定性,本文还构建了随机网络的拆借矩阵 [17] ,对于其拆借规模的估算同本文对于核心边缘网络拆解规模的估算方法,从而得到的拆借网络如图2(b)。图2中,各节点的数字代表第k个银行,节点尺寸的大小表示每个银行的出度入度之和,箭头粗细表示两个银行之间拆借额的权值,有阴影的节点表示这些银行之间的拆借关系比较密切。
由图2中两种网络可以看出,图2(b)节点的度分布比图2(a)均匀,图2(a)中拆借规模的分布比较均匀。
3.2. 边缘银行受到存款冲击的情况
根据3.1节的核心边缘网络模型,核心边缘网络结构中反应连接关系的邻接矩阵
的确定与核心银
Math_69#
(a) (b)
图1. 拆借规则说明
 (a)
(a) (b)
(b)
Figure 2. Interbank lending algorithm
图2. 拆借规则说明
行、边缘银行和连接度
有关。条件(c)中
与
如何组合影响着最终的邻接矩阵
,出于保护商业机密以及国家金融系统的安全,我们无法得到官方发布的银行之间的连接信息,所以规定
和
之间的连接方式为随机连接。仿真以3.1中16家银行(标号为1,2,…,16)为对象,对下面表2中不同核心银行数的四种情况进行仿真,并与随机网络结构仿真得到的数据进行比较。
根据表2,分别得到各种情况下的邻接矩阵
后,然后根据2.1节拆借网络模型构建方法来估算初始值
。对于不同的拆借关系矩阵
可以用熵来衡量其数据分布情况 [14] 。其他参数具体取值如下:系统初始银行数量是16家,仿真时间设置为200期,
,
,
,
,
,
,
,
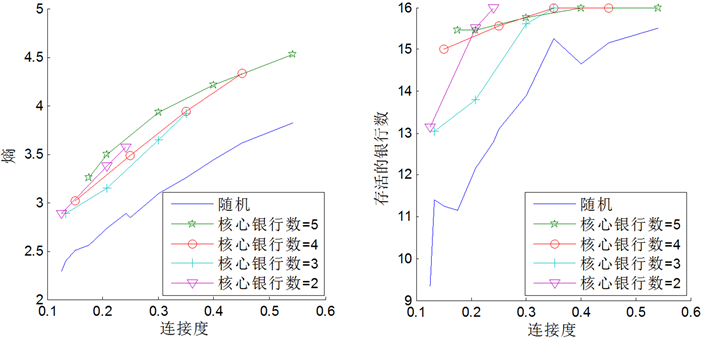
。当边缘银行受到冲击时,仿真结果如图3所示。
由此可以看出在不同连接度的情况下,核心边缘网络结构的熵值比随机网络的大(见图3(a)),并且核心边缘网络中最终的存活银行数比随机银行网络的多(见图3(b)),一定条件下受攻击的边缘银行甚至能成功解决流动性不足的问题保持银行系统的稳定性。这说明了,当边缘银行受到外部存款冲击时,核心边缘网络比随机网络要稳定。由于核心边缘网络中,每一个边缘银行的潜在贷款人至少是全部的核心银行,此外,边缘银行还能通过某一核心银行作为中介缓解另一个边缘银行的流动性危机。所以,当边缘银行因存款冲击而面临流动性危机时,核心边缘网络中该银行的潜在贷款银行数量比随机网络中的多,此种情况下核心边缘网络更稳定。

Table 2. List of core banks and periphery banks in four cases
表2. 四种情况下核心银行和边缘银行分布
 (a) (b)
(a) (b)
Figure 3. The stability of bank system when the periphery banks suffered deposits shocks
图3. 边缘银行受到存款冲击时的银行稳定性

Figure 4. The stability of bank system when the core banks suffered deposits shocks
图4. 核心银行受到存款冲击时的银行稳定性
3.3. 核心银行受到存款冲击的情况
而当核心银行受到存款冲击时,两种银行网络结构在面对相同存款冲击的稳定性如图4。(各参数设置同3.2)
图4所示,当一个核心银行受到存款冲击时,连接度小且核心银行总数少时,随机网络更稳定。连接度小但核心银行数大时,或者连接度大时,核心边缘网络更稳定。
图4中虚线的左侧显示,连接度小时,当核心银行数量为2或3时,随机网络更稳定。因为在核心边缘网络中,一个核心银行对于核心银行总数为2~3个的货币中心来说地位相当重要,一个核心银行受到存款冲击,面临流动性危机时,它不但不能帮助其它银行缓解流动性压力、分担风险,反而需要寻求其它银行提供贷款帮助。核心银行面临存款冲击时流动性缺口更大,在无外界救助仅依靠系统内其他银行对它进行救助的前提下,救助的结果无论是成功还是失败,系统都会变得不稳定。当连接度较小且核心银行总数少时,若救助失败,它的倒闭无疑也阻断了众多边缘银行与其它银行的连接,容易造成这些边缘银行也出现流动性不足危机从而倒闭。若救助成功,系统为满足其流动性缺口会造成整个系统中流动性资产减少,从而削弱了货币中心的作用,同样容易造成其他银行出现流动性不足危机。当连接度小且核心银行总数较多时,与单个核心银行直接连接的边缘银行平均数量减少了,单个核心银行的重要程度会降低,货币中心仍能发挥其作用,此时核心边缘网络更稳定。
图4中虚线的右侧显示,连接度大时,核心边缘网络较随机网络更稳定。因为连接度大的情况下,被冲击的核心银行倒闭后,与它直接连接的边缘银行与货币中心的其他银行存在连接的概率增大,因此这些边缘银行存在流动性不足的风险减小,系统相对更稳定。
4. 结论
本文构建了基于核心边缘网络拓扑结构的动态银行拆借网络系统模型,并结合随机网络结构下的系统模型,在随机网络和核心边缘网络两种拓扑结构下,对银行系统的稳定性问题进行了仿真模拟研究。结果表明:
1) 在边缘银行受到存款冲击的情形下,核心边缘网络的银行系统稳定性高于随机网络的银行系统。拆借资金在银行间的分布越均匀,即银行的平均风险越低越有利于分散风险,越利于提高银行系统的稳定性,系统越稳定。此种情况下监管部门应当防止银行之间过度集中的拆借交易行为。
2) 在核心银行受到存款冲击的情形下,当连接度小时,若核心银行总数少,随机网络更稳定,且拆借资金在银行间的分布越集中系统越稳定。此种情况下监管部门应视具体情况决定是否提供外部救助,如果拆借频繁的银行是受到冲击的银行时应选择救助,如果拆借频繁的银行不是受到冲击的银行时选择让银行间互助。但当核心银行总数大或连接度大时,核心边缘网络更稳定,且拆借资金在银行间的分布越均匀系统越稳定。
基金项目
国家自然科学基金项目(71371046)。