1. 引言
销售预测是生产,库存,以及销售计划的基础。规模越大的服装企业具有的产品品类,颜色或尺寸越多,这些对象都需要在制定计划前进行预测。此外,企业中往往存在多个决策者,从公司董事长到店长等角色,从运营,市场,销售及财务各个部门,都需要不同层面的销售预测来支持管理与决策。然而,长期以来预测的研究存在预测思路较为单一的情况,大部分预测主要集中于对预测算法的改进,且就销售预测而言,预测的对象也主要停留在某产品的销售额或总销售额,对于各层面之间的关系则较少涉及,只有较少学者在对电力行业的预测中涉及到多层次预测,如 [1] [2] 等。而在实际情况中应当注意到企业越来越细致的销售计划需求,以及各层面需求之间的联系,因此可以从分层次销售预测的角度来满足企业的需求。
销售数据多是按照相等时间间隔,如按季度,按月,按日等记录从而组成的时间序列数据,因此在做分层次预测时,将会出现多个时间序列,这些时间序列按产品属性,地区属性以及其他属性等按组聚集,形成一种层次结构,这种具有层次机构的时间序列数据称为层次时间序列数据 [3] 。如图例,为一个两层时间序列数据,下文建模将以该层次结构为例(图1)。
在对层次时间序列数据中所有时间序列进行单独预测后会发现,不同层次,比如低层数据序列的预测加总值并不等于较高层的预测值,这也就会导致不同的层面以及地方的管理者拿到的预测值不能统一。该现象是由于在预测过程中预测方法会不可避免的导致预测误差,从而导致不同层次的预测结果无法到达一致。因此,我们需要对具有层次结构的时间序列预测进行协调才能达到统一的预测结果,这就是Stone等人提出的著名的预测协调问题 [3] 。
目前最为普遍的协调层次时间序列预测的方式主要有以下两种,由上至下和由下至上的层次预测协调方式。这两种方式的使用可以追溯到1954年Wrighton等人 [4] 的研究。由上至下方法首先需要预测最
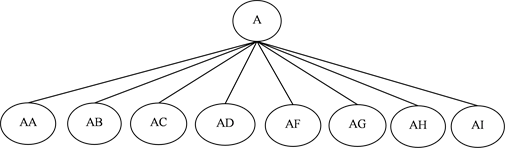
Figure 1. Structure of hierarchical time series
图1. 层次时间序列结构图
顶层的总数据序列,然后根据某种比例将预测值分解,得到下层预测值。目前使用最多的比例就是数据的历史比例。由下至上方法具体是指先对层次结构中最底层的子序列进行预测,然后通过简单的回归方式获取层次结构中较高层序列的预测值 [5] 。目前大部分层次预测研究重点也在于比较这两种方式在不同数据情况下的表现。此外,Hyndman等人在2011年时提出了一种优化的层次预测方式 [5] ,并在继续在此基础上进行拓展与优化 [6] 。该优化方法是基于所有层次上所有时间序列的预测值进行的,对各序列进行建模预测后,使用回归产生新的一系列调整后的预测结果。
本文经过研究后发现,各层次预测方式各有利弊,目前国内暂无文献对于服装企业销售进行分层次时间序列预测研究。然而服装行业竞争日渐激烈,若企业无法细化服装预测也就无法做好销售计划及库存准备。另外,如何实现各层次预测结果的协调也是需要探索的。简单的由下之上及历史比例分配,主观性及对过去的依赖性太强。本文提出基于底层预测值比例的由上至下法并结合最小二乘协调思想 [5] ,探究层次时间序列数据的预测协调,后根据真实的服装企业销售数据进行验证。同时对新方法以及由上至下和由下至上法进行比较,发现本文方法在保证预测结果统一的情况下,其平均预测精度也有所提高。
2. 整体算法及流程
1) 收集待预测服装销售历史数据;
2) 处理数据,将销售数据按照服装品类进行整理;
3) 对服装总销售额以及各服装品类销售额进行按季度的销售预测;
4) 分别运用由上至下,右下至上,以及按底层预测值比例改进的由上至下法和基于最小二乘思想及底层预测值比例的层次协调预测法,处理上一步得到的预测值;
5) 得到服装品类维度上下层统一的季度销售预测值,作为最终的预测结果。
2.1. 由上至下及由下至上方法
假设对于一个层次时间序列模型,共有k个层次,其中层次
,第K层是最底层的时间序列。综上,层次中所有时间序列的个数为
,其中
代表i层上时间序列的个数。观测时间点
,本文将对每层序列未来
的时间点进行预测。对于每一个层次中的每一个时间序列有如下定义,对于该层次时间序列,
,产品时间序列
,序列x在t时刻的观测值
,序列x在t时刻的预测值
,序列x在t时刻协调后的预测值
,t时刻总序列观测值
,t时刻总序列预测值
,t时刻总序列协调后预测值
,t时刻层次i上所有序列的观测值序列集合
,t时刻所有观测值序列的集合,
,
,t时刻层次i上所有序列的预测值序列集合
,t时刻所有预测值序列的集合,
,
,t时刻层次i上所有协调后的预测值序列集合
,t时刻所有协调后的预测值序列的集合,
,
,以
为结构的求和矩阵
由于具有层次结构的时间序列数量往往较多,因此在预测过程中使用矩阵和向量表达式可以简化运
算,
为t时刻层次 上所有序列的观测值,因此,
综上,定义如下:
其中,
是以
为结构的求和矩阵,作用是将聚集最底层的序列值。
例如根据图5-1,
,
是以9 ´ 8为结构的聚合矩阵,
 结构为
的单位矩阵
结构为
的单位矩阵
从矩阵
的结构可以看出,其可根据层次结构的层来划分。矩阵的第一行是以
为长度的单位向量,下层部分是为
的单位矩阵。
2.1.1. 由上至下
由上至下的层次预测方式整体思想即先对顶层序列数据进行预测,再根据一定比例拆分至下层序列,即为下层序列的预测值,无需对子序列进行预测,因此,母序列的预测值一定等于子序列。该方法最后调整后预测值的精确性取决于拆分比例的选择。
定义
为序列x在t时刻的拆分比例。目前,大部分学者以及企业中使用的拆分比例
是按照某产品的历史平均销售额占历史平均总销售额的比例进行拆分。其公式如下:
在本文研究中,取预测点前三年的历史销售数据进行比例的计算。
因此,
(2)
其中
2.1.2. 由下至上
由下至上的层次预测法也是层次结构时间序列预测调整的最常用的方法之一,它的基本思想是首先对最底层时间序列数据进行预测,再使用求和矩阵提取底层序列预测信息,从而得到上层时间序列预测值。
综上,由下至上定义如下:
(3)
因此,
由上述矩阵即可得到所有层次基于最底层预测值的由下至上加和预测值。
3. 层次时间序列预测新方法
3.1. 基于底层预测值比例的由上至下法
考虑到实际预测值更能反映低层产品未来可能在销售中的占比,本文提出新的由上至下的分配比例
代替历史销售数据比例,该比例反映该产品销售额预测值占该产品所在层次所有产品销售额的预测值,其定义如下:
其中
为产品x所在层所有产品直接预测值的和。
综上,
(4)
其中,
。
3.2. 基于底层预测值比例及最小二乘法的层次预测协调法
以上两种传统的层次时间序列数据预测仅需要在预测某一层的预测值后得出其他层次的预测值,即达到层次间协调的效果。然而分别就这两种方式来说,首先是上至下方法,通常情况预测出的结果不太准确,准确性完全取决于比例的选取,这是由于顶层数据一般更为平滑,因此在按比例分解过程很难真实的反映出下层数据的波动性及季节性。而由下至上方法通常是加和,当低层数据表现出相似的季节性及波动性时,该方法的效果才会比较好,否则,效果不好。
因此,本文根据Hyndman [5] [6] 对所有层次结构中的时间序列预测后再进行协调的思想,提出一种基于底层预测值比例及最小二乘思想协调各层预测结果的方法,目的是利用层次结构中的所有时间序列以达到更好的协调效果。在预测协调过程中,各品类销售额预测值直接相加应等同于直接对总销售额预
测的结果,即
,而实际情况中是存在
。预测协调的目标是计算各销售额预测值
的得到最优的协调值
。因此,利用最小二乘法思想,再结合上述按底层预测值比例进
行分配的思想,在协调的过程中使得相对协调值的加权平方和达到最小的即为各层次序列预测的最优协调值。其数学模型为:
(5)
式中,
表示权重,表示各品类预测值占该层所有品类预测值的占比,
,总销售额预测
值占比为
,可见第i个品类预测占比越大,权重越大。
和
分别为总销售额预测协调值及子销售额预测协调值。该式为典型的等式约束二次规划问题,可应用拉格朗日乘法求解 [7] 。
(6)
(7)
式中
为总销售额与品类销售额预测间的不协调量,可以看出预测协调问题仅与预测结果有关,与原始销售额无关,实际为对不平衡量的重新分配问题,按照一定权重,因此本文选用底层预测值占比,进行预测结果的重新协调,以达到最优协调值。
4. 实证研究
为探究四种方法在层次时间序列服装销售预测上的准确性,本文以某服装企业的真实服装季度销售额为例进行验证。该企业销售数据按产品属性被分为两层,第一层为总销售额,第二层为八种服装品类销售额,分别为附件,毛衣,短裤短裙,牛仔裤,裤子,衬衫,T恤和外套。首先分别预测四个季度(如2015年第二季度,以下记为201502,以此类推)的总销售额及各品类销售额,表1为预测结果。
由表1可知,各服装品类销售额预测值与总销售额预测值之间存在一定差异。比如,2015年第二季度8个服装品类预测之和为73479849.63万元,而总销售额预测值为74788359.10万元;2015年第三季度8个服装品类预测之和为62873219.19万元,总销售额为62040239.18万元,其他两个季度的预测结果存在的情况也相同。因此,需要对以上两个层次的预测结果进行修正协调。
由于本文对以上四个预测点进行了四种方法的协调预测,因此数据较多,表二将以201502季度为例,展示四种方法协调后的预测结果。(表中p为按历史比例,p'为按底层预测值比例,最小二乘即基于最小二乘思想的协调法)由表2可见,通过使用四种层次协调法后,各品类协调后预测值之和等于总销售额协调后的预测值,达到了品类维度上下层统一的结果,协调有效。然后,通过计算各方法对四个预测点预
测后的平均绝对百分比误差
,比较协调效果,其中
为实际值,
为预测
值,
为样本量。
由表3可见,四种方法使用结果是,用传统按历史比例得到的各层次平均MAPE最高,也就是误差最大,而基于最小二乘思想及底层预测值占比的方法取得的协调效果最好。可以看到由下至上的方式效果也是不错的。那么就由上而下方法而言,本文提出的按照底层预测值比例进行分配的效果明显优于传统的按照历史比例进行分配。由此可见,本文使用的两种新的层次时间序列的协调法是切实有效的,希望对企业销售预测提供新的思路和依据。

Table 1. Direct forecasting value of apparel categories and gross sales
表1. 服装各品类及总销售额直接预测值

Table 2. Coordinated forecasting values of apparel categories and gross sales
表2. 服装各品类及总销售额协调后预测值

Table 3. Average MAPE of each hierarchy
表3. 各层次平均绝对百分比误差MAPE
5. 结论
本文围绕层次时间序列数据预测协调问题,构建了四种层次预测协调模型,并通过对服装企业真实销售额进行实证分析。主要是分别对各服装品类以及总销售额进行预测,形成了层次预测结果,并利用各层预测之间的关联建立层次协调模型,实现了层次预测结果的统一性。四种层次预测协调法的效果对比后发现,本文方法能够在确保层次预测结果统一性的基础上,提高协调预测的准确性。
相较于传统的销售预测片面研究预测模型而言,本文更注重各层次销售数据之间的联系,为企业各层面更细化的销售计划提供思路。