基于GARCH模型的融资融券对我国股市的影响研究

A Research about Effects Margin Transaction Has on the Stock Market in China Based on GARCH Model

摘要: 选取2014年3月12日至2016年9月14日之间的619个上证综指的对数收益率以及上交所的融资、融券余额作为样本数据。首先，利用AIC和SC准则确定了GARCH模型的滞后项数；然后，引入虚拟变量作为牛、熊市的划分，建立含虚拟变量的GARCH(1,1)模型，分析融资融券制度对股市波动性的影响。结果显示：1) 融资交易在熊市和牛市均增加了股市的波动性，并且融资交易在熊市时对股市波动性的放大作用比在牛市时更大；2) 融券交易在牛市时，增加了股市的波动性，而在熊市时，对股市的波动性有抑制作用。最后，结合当时的制度、政策及投资者心理，从统计上分析得到：在我国融资融券业务发展不均衡，融资业务规模远远大于融券业务的规模，因此，我国两融业务对股市波动性最重要的影响是融资业务。

Abstract: Select 619 logarithmic ratio of Shanghai Composite Index and balances of financing and securities loan during the period between 12th March, 2014 and 14th September, 2016 as sample data. Firstly, AIC and SC criteria are used to confirm the lag item numbers of GARCH model. Then, we introduce dummy variables as the partition of bull market and bear market, establish GARCH (1,1) model including dummy variables and analyze the effects that the system of margin transaction has on stock market volatility. The results indicate that: 1) Financing transaction in both bull market and bear market increases stock market volatility and the amplified influence that financing transaction has on the volatility in the bear market is more significant than that in the bull market. 2) Securities trading increases the volatility in the bull market while restrains that in the bear market. Finally, we combine the temporal systems, policies and investors’ mentality and from statistical analysis, we draw a conclusion: In China, financing business and securities business develop unevenly and the scale of financing business is far larger than that of securities business. Thus, in China, financing business exerts more important effects on the fluctuation of the stock market than securities business.

1. 引言

融资融券交易又被称为“证券信用交易”或是保证金交易，是证券市场一项普遍和成熟的交易制度。融资交易即为投资者在看涨股市行情时，向具有业务资格的证券公司提供相关的担保物，并约定好还款利息和还款期限，从证券公司借出资金，购买证券，在还款期限即将到期时，再卖出标的债券，还清所欠证券公司的本息。融券交易则为投资者在看跌股市行情时，向证券公司提供担保物或资金，借出一定数量和品种的证券，在约定的归还期限到来时，再买入相同数量和品种的债券归还证券公司。融资融券交易制度，在国外尤其是发达国家已经发展成为一项基本的信用交易制度。而在中国，融资融券交易起步较晚，直至2010年3月31日，上海和深圳证券交易事务所才放开融资融券交易的申报。在经历了四年的缓慢升温后，至2014年下半年，A股市场的融资融券交易开始呈现爆发式增长。据统计2013年底，融资融券余额为3456亿元，而到2014年12月19日已经达到10001亿元，突破万亿大关，不到一年时间增加6545亿元(http://www.qhrb.com.cn/2016/0221/192493.shtml)。与此同时中国股市节节攀升，到2015年6月12日上证综指最高达到5178点，而在这之后中国股市又步入“千股跌停”的熊市(最低时跌破2800点)。融资融券业务对我国证券市场的这种大起大落是否起到了推波助澜的作用？融资融券对我国股市波动性究竟会产生什么样的影响？显然对这些问题的研究，有助于规范、优化不同金融工具在证券市场的合理应用，规避系统性风险的发生，本研究正是基于此而展开。

2. 文献综述

融资融券交易对股票市场的运行会产生怎样的影响？是否会加大股票市场的波动性？综合目前国内外学者的理论研究和实证分析发现，针对这一问题学界还没有得到统一的结论。在欧美等发达国家，融资融券业务起步较早，所以对融资融券制度的研究也相对较早。早在1976年，美国著名经济学家Lintner (1971) [1] 就指出在完美市场的条件下，个人投资者的平衡头寸在任意的市场价格的情况下，对卖空所需的担保金和保证金要求具有不变形，这就说明理论上，融资融券机制对市场波动性是不会构成明显影响的。之后，Kim (1996) [2] 通过建立Schwert模型和GARCH模型对新加坡的股票交易市场进行研究得出结论：在融券交易被限制的情况下，股市波动性上升，这就意味着融券能够有效地抑制市场的波动性。另一方面，Brish和Goerzmann (2007) [3] 通过对全世界46个股票市场进行分类研究，将这些股票市场分为已经实施做空机制的市场和未实施做空机制的市场，通过比较分析得出已经实施做空机制的市场比未实施做空机制的市场有更大的风险，即融资融券机制放大了市场的波动性。另外地，Sobaci，Sensoy和Erturk (2014) [4] 在2014年通过建立VAR的衍生模型研究了土耳其市场从2005年1月到2012年12月的融资融券交易和股市波动性的动态关系，得出了完全相反的结论，即：做空交易的增加会和市场风险的降低联系在一起，但是这种联系在2008年金融危机时被大大削弱。Bohl,Reher和Wilfling (2016) [5] 在2016年建立了非对称的Markov-switching GARCH模型，在2008年9月到2010年7月德国对金融公司实行禁止做空的法令的背景下，对德国股票收益的波动性做了研究。研究证据表明：金融危机加大了市场风险，尤其加大了那些受做空限制影响的股票的风险，他们认为这是做空机制受限增大股市波动性的证明。

我国国内的一些学者针对我国融资融券机制对股市波动性影响的一些研究总体来说，有以下三个观点：1) 融资融券制度会增强市场的稳定性，从而减小市场波动性。比如说，王虎，朱贵宇(2012) [6] 采用上证50指数的每日股票价格收盘指数作为研究对象，通过建立GARCH模型得出了融资融券交易业务有效地稳定了股市的结论。另外地，冯玉梅，陈璇和张玲(2016) [7] 通过以沪深300指数作为样本构建VAR模型和进行脉冲响应分析得出了融资融券转常规后能够平抑股市的波动，但是这种抑制作用目前较小。2) 融资融券制度会加剧股市的价格波动。比如说，吴国平和谷慎(2015) [8] 采用流通股加权方法，重新编制融资融券指数，建立了含有虚拟变量的VAR模型和GARCH模型比较了融资融券业务推出前后股市波动性的变化，最后得出融资融券业务总体上加剧了股市的价格波动。3) 第三种观点是：融资融券制度不会对股市的波动性产生显著影响。比如说，张兰兰(2016) [9] 首先通过建立VAR模型分析一个内生变量对其他变量的影响情况，再引入脉冲响应函数进行方差分解分析对该问题进行进一步分析，最后通过格兰杰因果检验得出市场波动性和买空、卖空交易，也就是融资融券交易的相关关系不强的结论。另一方面，倪伟佳(2013) [10] 通过建立TGARCH模型得出由于我国股市融资融券规模较小，股市波动性的变化并不能有效解释融资融券交易的变化。

在我国股票市场，融资融券业务推出时间较短，之前受样本数量限制，相关研究得出了一些短期的实证分析结果。本文旨在前人研究的基础上，以2014年3月12日至2016年9月14日上证综指为样本，通过建立GARCH模型研究融资融券对股市波动性是否存在影响。本文的创新之处在于：第一，研究选取的时间段为一特殊时间段。其特殊性在于该时间段股市先经历“千股涨停”的牛市，然后又经历“千股跌停”的熊市。同时这个时间段的起始也恰好是融资融券制度在经历了几年缓慢升温后，开始爆发式增长的时间段。这次“牛”、“熊”市是我国证券市场正式开通融资融券交易系统以来，我国股市第一次经历带“资金杠杆”的牛市和熊市，因此对其研究将对我国未来的融资融券制度的发展和完善以及对我国未来股市波动性的预测都有重要意义；第二，本文采用的是GARCH模型来进行研究。本文之前的一些研究，对这一特殊时间段的融资融券交易对股市波动性的影响研究大多采用VAR模型以及其衍生模型(如VEC模型)。GARCH模型能够很好地刻画股市波动性的“波动集群的特征 [11] 。GARCH模型的引入无疑对该问题的研究提供了一种新的方法。第三，考虑到了融资融券交易在熊市、牛市时对股市波动性的影响可能存在结构性差异，故本研究引入虚拟变量，建立一个统一的模型，既可分析融资融券在熊市和牛市时对证券市场波动性的影响，又便于比较它们的差异。第四，本文还通过具体分析当时的融资融券制度、政府政策、媒体信息、投资者心理等因素，对GARCH模型的估计结果进一步作了相关的统计分析，这可为相关职能部门在以后设计推出金融工具时，因时、因人相机决策提供思路。

3. 实证分析

3.1. 样本选取和变量定义

中国股市从2014年至2016年经历了“疯牛”到“股灾”的巨大股市波动，同时2014年也是融资融券突飞猛进的一年，故我们选取2014年3月12日到2016年9月14日上证综指共计619个样本数据，分析融资融券制度对这一时间的股市波动性的影响(数据来源：国泰安数据库)。根据股市进程，我们以2015年6月12日为时间节点，定义2014.3.12~2015.6.12为牛市阶段，2015.6.15~2016.9.14为熊市阶段，将样本区间划分为两个时间段来研究。沿用文 [12] 的定义，在本文中，用融资余额代表融资交易的影响力，用融券余额代表融券余额的影响力，引入三个变量：

Vol表示“股市波动性”；RZ表示“融资余额(亿元)”；RQ表示“融券余额(亿元)”

其中，股市波动性Vol用上证综指的对数收益率表示，即： $Vol=\ln \left(P_t/P_{t-1}\right)$ 。本研究所用统计软件为Eviews 8.0.

3.2. 模型的建立和估计

为建立GARCH模型，先对样本数据的正态性、平稳性和相关性进行检验。

3.2.1. 正态性检验

本文采用Jarque-Bera法对上证综指的日对数收益率作正态性检验。结果如表1所示。

从表1可以看出，峰度系数为 $7.495>3$ ，偏度系数为 $-1.184<0$ ，JB值为666.8，且相应的概率值为0，在1%的显著性水平下，说明该分布不服从正太分布，上证综指的对数收益率分布具有尖峰厚尾的特征，且重尾在左侧，该分布左偏。

3.2.2. 平稳性检验

通过描点可知上证综指的日对数收益率没有时间趋势也没有截距项，故选择不含截距和斜率的模式对样本数据进行ADF检验，结果如表2所示。

Table 1. Normal test results

表1. 正态性检验结果

Table 2. Stationarity test results

表2. 平稳性检验结果

从表2得出的结果来看，上证综指的对数收益率序列的ADF统计值为−5.95，在各显著性水平下，均小于临界值，且伴随概率P值为0。所以可以得出，在1%的显著性水平下，拒绝原假设，即该时间序列没有单位根，是平稳的时间序列。

3.2.3. 相关性检验

在建立GARCH模型的均值方程之前，首先要对被解释变量的时间序列进行相关性检验。通过计算上证综指的日对数收益率序列的自相关和偏自相关系数，可知在滞后项为1阶、2阶、3阶时都落入两倍的估计标准差内，且其对应的Q统计量的伴随P值均大于0.05，故序列在5%的显著性水平下，不存在明显的自相关性。

3.2.4. ARCH效应检验

由相关性检验知，序列不存在显著的相关性，所以，将均值方程设置为只含残差项和常数项的模型即可：

$Vo{l}_t=C+{\epsilon }_t$

其中，C为常数项， ${\epsilon }_t$ 为残差项。

然后将序列 $Vo{l}_t$ 去均值化(将原序列的值减去序列的均值)，记得到新的序列 $W_t$ 。由于建立的均值方程不是ARMA模型，在统计软件中没有直接的LM法，因此我们采用对残差的平方相关图检验的方法。首先，生成 $W_t$ 的平方序列 $Z_t$ ( $Z_t=W_t^2$ )；其次，对 $Z_t$ 序列进行自相关和偏自相关的检验。检验结果如表3所示。由表3可知，该序列存在明显的相关性，所以有ARCH效应，可以建立GARCH模型对其进行修正和估计。

3.2.5. GARCH模型的建立及估计

Engle在1982年首次提出了ARCH模型(自回归条件异方差模型)该模型可用来刻画波动率的聚集特征及收益率的厚尾特性。但由于其自相关系数高并缓慢衰减的特征，ARCH(q)往往需要较大的q才能刻画资产收益率波动率的变化。T.Bollerslev于1986年提出了广义ARCH(GARCH)模型进行改进，它能以非常简约的形式刻画波动率的高阶自相关性以及资产收益率的厚尾特征。 [11] GARCH模型的一般表达式是含有q个ARCH项和p个GARCH项，即GARCH(p,q)：

${\sigma }_t^2={\alpha }_0+{\lambda }_1{\sigma }_{t-1}^2+\cdots +{\lambda }_p{\sigma }_{t-p}^2+{\alpha }_1{u}_{t-1}^2+\cdots +{\alpha }_q{u}_{t-p}^2$

GARCH(p,q)应满足的条件是 ${\alpha }_0>0,{\alpha }_i\ge 0,i=1,2,\cdots ,q,{\lambda }_i\ge 0,i=1,2,\cdots ,p,0\le {\displaystyle {\sum }_{i=1}^q{\alpha }_i}+{\displaystyle {\sum }_{i=1}^p{\lambda }_i<1}$

为确定GARCH模型的阶数，由 $Vo{l}_t$ 的AC和PAC图尝试分别建立GARCH(1,1)、GARCH(1,2)、GARCH(2,1)、GARCH(2,2)模型。表4给出了这4个模型的拟合结果，根据AIC和SC准则以及显著性原则，最后选定GARCH(1,1)模型是最合适的模型。

为了研究融资融券工具对股市波动率是否存在显著影响，我们在GARCH(1,1)模型中加入RZ和RQ变量。同时，为进一步分析融资融券工具对股市“牛市”、“熊市”的影响是否存在差异，我们引入了虚拟变量：

Table 3. Correlation test of sequence Z

表3. 序列Z的相关性检验

注：“^*”“^**”“^***”分别表示该系数在10%，5%及1%的水平下显著。本文其余表中记号同此。

Table 4. Selection of the GARCH model

表4. GARCH模型的选择

$D_t=\{\begin{array}{l}0,\mathrm{2015.06.12}以前，\\ 1,\mathrm{2015.06.12}以后.\end{array}$

最终建立GARCH(1,1)模型如下：

$\{\begin{array}{l}Vo{l}_t=C+{\epsilon }_t\\ {\epsilon }_t={\sigma }_t{u}_t,u_t~iid{\rm N}\left(0,1\right)\\ {\sigma }_t^2={\alpha }_1+\alpha {\epsilon }_{t-1}^2+\beta {\sigma }_{t-1}^2+{\alpha }_2{D}_t+{\beta }_{1}R{Z}_t+{\beta }_{2}R{Q}_t+{\beta }_3\left(D_{t}R{Z}_t\right)+{\beta }_4\left(D_{t}R{Q}_t\right)\end{array}$ (1)

其中， ${\alpha }_1$ 为常数项， ${\epsilon }_t$ 为残差项。(1)式代表的含义分别如下：

当处于熊市时，即虚拟变量 $D_t=0$ 时，GARCH模型的形式则变为：

${\sigma }_t^2={\alpha }_1+\alpha {\epsilon }_{t-1}^2+\beta {\sigma }_{t-1}^2+{\beta }_{1}R{Z}_t+{\beta }_{2}R{Q}_t$ (2)

当处于牛市时，即虚拟变量 $D_t=1$ 时，GARCH模型的形式则变为：

${\sigma }_t^2=\left({\alpha }_1+{\alpha }_2\right)+\alpha {\epsilon }_{t-1}^2+\beta {\sigma }_{t-1}^2+\left({\beta }_1+{\beta }_3\right)R{Z}_t+\left({\beta }_2+{\beta }_4\right)R{Q}_t$ (3)

对比上面的式(2)和式(3)，可以看出， ${\alpha }_2$ 为截距差异系数，它代表的是相对于熊市来说，牛市对股市波动性的平均影响。 ${\beta }_3,{\beta }_4$ 为斜率差异系数，其中， ${\beta }_3$ 代表的是在熊市的基础上，处于牛市的融资交易对股市波动性的影响，也就是说牛市的融资交易相对于熊市的融资交易对股市波动性的影响的差异。同样地， ${\beta }_4$ 代表的是在熊市的基础上，处于牛市的融券交易对股市波动性的影响。对GARCH模型的回归结果如表5所示。

以上常数项和相应参数的系数的P值均小于0.1，且大部分在1%的显著性水平下通过t检验，这说明GARCH模型的方差方程中的参数和常数项的设置均有意义，即这些变量对波动性均产生显著影响。又因为在条件方差方程中，GARCH项和ARCH项的系数和为0.947 < 1，满足GARCH(1,1)模型的约束条件。

从估计结果可以看出，ARCH项的系数为正，说明股市前一期的波动信息对本期的波动性存在正的影响。GARCH项表示前一期的波动性对本期波动性的影响，系数越大，表示对条件方差的冲击性越持久。由估计结果得，GARCH项的系数为正，且达到了0.91，数值较大，说明前一期的波动性对当期的波动性存在着较大的正的影响。之后的分析我们以虚拟变量 $D_t$ 的取值分成两部分，在之前的假定中，当虚拟变量 $D_t=0$ 时，即表明股市为熊市，首先对熊市的情况进行分析，在估计结果中， $R{Z}_t$ 的系数 ${\beta }_1$ 为正，说明在熊市时，融资交易行为增加了当时股市的波动性。另一方面， $R{Q}_t$ 的系数 ${\beta }_2$ 为负，说明在熊市时，融券交易减少了当时股市的波动性。下面考虑当虚拟变量 $D_t=1$ 时的情况，即股市为牛市时，首先虚拟变量 $D_t$ 的系数为正，说明相较于熊市来说，当处于牛市时，股市的波动性会增加。 $D_{t}R{Z}_t$ 的系数 ${\beta }_3$ 为负，但是 ${\beta }_1+{\beta }_3$ 的值仍为正值，说明总的来说，牛市的融资交易行为会增加股市波动性，但这时它对股市波动性的影响不如它在熊市时的影响大。 $D_{t}R{Q}_t$ 的系数 ${\beta }_4$ 为正值，且 ${\beta }_2+{\beta }_4$ 的值也是正值，说明总的来说，牛市的融券行为会增加股市的波动性。下面通过表6，来展示以上文字叙述的结果。

Table 5. The regression results of the GARCH(1,1) model

表5. GARCH(1,1)模型的回归结果

Table 6. Analysis results of GARCH model

表6. GARCH模型的分析结果

其中：“+”表示增加股市波动性，“++”表示比“+”更加强的正影响，“-”表示减少股市波动性。除此之外，从模型中，我们还可以看出，2014至2015年的牛市比2015年至2016年的熊市波动性更大。

3.2.6. GARCH模型的结果解释

从GARCH模型得到的分析结果来看，融资交易比融券交易更能加剧股市的波动性。从上证综指历年的融资、融券余额数据可以看出，融资余额都要远远大于融券余额，以2014年3月12日为例，当天的融资余额为8780.76亿元，而融券余额仅为31.82亿元，融资交易余额是融券余额的283倍，并且随着时间的推移，两融业务的差距也越拉越大。导致这一现象的根本原因是我国的做空机制(融券机制)相比发达国家的金融市场还不成熟。在我国，融券需要投资者向券商借入债券，券商在融券业务中是占据主导地位的，而我国券商持有的券源并不充足，所以就算是在熊市，有很多做空机会，投资者也会面临融不到券的窘境。其次，我国投资者普遍有着“追涨杀跌”的投资心态，大部分投资者都不愿意承担做空头的风险。这两点就会造成融券交易的规模在我国十分有限，所以它对股市波动性的影响相对于融资交易就很小。所以，这也解释了，即使当2015年~2016年股市处于熊市时，融券交易确实降低了股市的波动性，但由于我国融券交易规模较小，它带来的对股市波动的抑制作用也是十分有限的。

从融资交易的角度来看，在2013年4月之前，根据国家的融资融券的管理条例，只有达到或是超过50万元的客户才有资格进行融资融券交易，然而满足这类要求的客户在沪深两市仅占5%。在2013年4月，国家降低了融资融券的门槛要求，允许证券公司按照自己服务的投资者的特性设置适当的门槛。证监局对融资交易的放开，使得投资者的举债能力增加。而随着股市回暖，投资者对当时股市的预期普遍偏高，且投资者也受当时主流媒体所传达的乐观信息所影响，如“改革牛”、“政策牛市”等。所以，投资者利用融资交易以极高的杠杆进行融资(如1:5，1:10甚至更高)。这样就带来极大的杠杆风险，这样就解释了在牛市时，融资交易对股市波动性有增强和放大的作用。我们绘制了从2013年12月到2016年8月的融资余额(取每月的最后一天的融资余额作为当月的融资余额)的趋势图，如图1。

从图中可以看出，从2014年下半年开始，上交所的融资规模发生了爆发式的增长，从2014年初的2000多亿元飞涨至2015年6月的近14000亿元，且这个时间段刚好与我们划定的牛市时间段吻合。而在2016年6月之后，融资余额发生了断崖式的下跌。另外，这与我们所划定的熊市时间也正好吻合。并且我们还做了上证综合指数与上交所融资、融券余额的相关性分析(表7)，以及上证综合指数和融资余额的时间趋势图(如图2)。

Table 7. Correlation analysis of the Shanghai composite index with the total amount of financing and short selling

表7. 上证综指与融资、融券总额的相关性分析

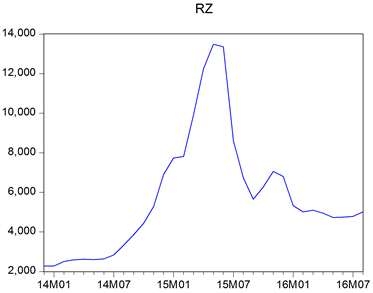
Figure 1. Monthly variation tendency of balance of financing

图1. 融资余额的时间趋势图

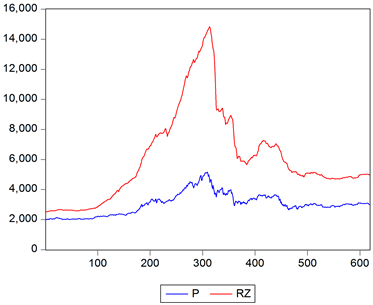
Figure 2. Daily variation tendency ofShanghai Composite index and balance of financing

图2. 上证综指和融资余额的时间趋势图

从表7中可以看出，上交所的融资余额和上证综指的相关性极高到了0.95，而融券余额和上证综指并没有明显的相关性。而从图2中可以看出，上交所的融资余额和上证综指的走势基本相一致，说明在我国，融资融券制度主要是融资业务在对股市的波动性造成影响，融券业务对我国股市的影响较小。我们知道，一个理性的投资人，会在股市行情看涨时，进行融资交易，而在看跌股市行情时，进行融券交易。而在我国，大多数的投资者都是非理性投资者，他们的投资方式都有明显的“追涨杀跌”的特征，他们在处于牛市时疯狂地买入，一旦股价下跌，造成恐慌，他们就迅速地抛售手中持有的股票。正是我国投资者的这种投资习惯，限制了融资融券制度对股市波动性的调节作用。

3.3. 总结与政策性建议

3.3.1. 总结

本文以上证综合指数的日对数收益率代表股市波动性，用上交所的融资余额和融券余额分别代表沪市的融资规模和融券规模，并且以2014年3月12日~2016年9月14日的数据为基础，并以2015年6月12日，上证综指暴跌这一事件为时间节点，建立了引入了虚拟变量的GARCH模型，来研究融资融券制度在熊市和牛市时对股市波动性的不同影响并得出了以下结论：

1) 从融资交易的角度来说，在牛市时(2014.3.12~2015.6.12)，融资交易增加了股市的波动性。这是因为融资交易带来了资金杠杆，使得盈亏放大，人们在股市行情较好的情况下，纷纷进行融资，加大杠杆，从而带来了极大的杠杆风险。而在这次熊市时(2015.6.15~2016)，融资交易也增加了股市的波动性，且这种波动性和在牛市是非对称的，模型结果显示，在熊市时，融资交易能给股市带来更大的波动性。

2) 从融券交易的角度来说，在牛市时，融券交易加剧了市场的波动性。而在熊市时，融券交易能够对股市波动性起到抑制的作用。然而，现实情况是在2015~2016年的熊市时，股市波动性依然很大，上证综指一路暴跌，这也从侧面说明了，在现阶段，我国的融券制度对股市波动性的抑制作用十分有限。

3) 从两融交易总体来看，两融业务开展时间较短，2010年3月31日才刚刚起步，我国的融资融券交易还存在着很多问题。第一，融券业务和融资业务发展极为不均衡，其中融资业务占主导地位，所以两融业务对股市波动性的影响，主要是融资业务对股市波动性的影响，也就是说在短期内，两融业务会增强对股市波动性，且在熊市时，两融业务对股市波动性的放大作用会比牛市时大。第二，目前融资融券业务的门槛依然很高，个人账户的开户的基本条件是在过去20个交易日中，账户日均资产满50万元。但是我国大部分个人投资者持股市值集中在10万元以下，截至2016年2月，我国持股市值在50万元以上个人投资者仅占总数的4.83% (数据来源：中证登，申万宏源研究)。第三，我国的个人投资者习惯于单边做多投资思维。投资者习惯于投资其看涨的股票，而不习惯于做空交易。

3.3.2. 政策性建议

1) 有序推进融资融券标的股票的扩容。之前我们分析到，我国融券规模较小的原因之一是证券公司券源有限，推进标的股票的扩容，可以促进融券业务的进行，避免投资者想融券却无券可融的局面。在一个健全的融资融券制度中，是否应该融券的标准应该是是否看跌股票价格而不是是否有券可融。

2) 适当降低融资融券的门槛。目前，我国的融资融券门槛是50万元。这个门槛对于个人投资者过高，而个人投资者占股市总投资者的99.71% (截至2016年2月)。应该鼓励证券公司根据自己客户的实际情况，设定自己的门槛，但是同时也要对证券公司设置的门槛实施强有力的监控，避免像2014年~2015年牛市期间那样，投资者以过高的资金杠杆进行融资的情况。

3) 加大对融资融券交易理念的宣传和教育。我国大部分投资者仍属于非理性投资者，应该鼓励证券公司对客户进行普及性的融资融券理念的教育，尽量使客户的投资观念趋于理性，这样做有利于投资者进行融资融券并用的双向投资，而非仅仅执着于融资的单向投资，能够很好地改善两融业务发展极不均衡的情况。

基金项目

本文获得江苏省“第二批中外合作办学高水平示范性建设工程项目培育点”(苏教办外[2017]14号)资助。