1. 引言
近年来,随着社会经济的发展,由拥挤或突发事件引起的公共安全问题逐年增加,行人的安全疏散问题引起了许多学者的广泛关注 [1] 。一般情况,行人流疏散模型可以分为两类:宏观模型 [2] [3] 和微观模型 [4] [5] ,其中微观模型又分为三种:社会力模型 [4] [5] [6] ,元胞自动机模型 [7] [8] [9] [10] 以及格子气模型 [11] [12] [13] 。
元胞自动机通过模拟系统中个体微观行为特征,在个体间相互作用条件下,实现系统整体宏观行为特征的研究 [14] 。杨立中等 [15] 基于“地场”方法,引入“位置危险度”的概念来确定人员运动规则,再现了火灾发生时人员的逃生过程。郑美容 [16] 基于元胞自动机对人员疏散行为进行了模拟研究,为疏散策略的选择提供了一些参考数据。林煌涛 [17] 对高校礼堂人群疏散进行了仿真,找出了礼堂人群疏散规律。王浩 [18] 建立了地铁站行人疏散仿真模型,并分析了地铁车站行人安全疏散的可靠性。张艳芬 [19] 建立了大型客运站应急疏散模型,并进行实例仿真研究,分析评价仿真结果,提出优化方案。姜子港 [20] 对某商场在紧急情况下人员的安全疏散进行了研究,重点讨论了借用防火分区防火门进行疏散对疏散效率的影响等。
上述研究对象及范围大多围绕地铁、体育馆、客运站、大型商城、室内等场所的一般性群体。事实上,特殊群体如踩踏事故的高发对象——中小学生群体、有听力视力障碍的人群、行动不便的残疾人或老人等,在面对突发事故,这些人群往往表现出异于一般行人的更为复杂的心理行为特征。田玉敏等 [21] 研究了特殊人群疏散行为,提出了需要深入研究特殊人群的疏散行为规律,以及根据人群特点进行有针对性的设计。薛李生辉等 [22] 研究了考虑个体差异的改进人群疏散模型,发现了人群中处于弱势的老人和儿童,由于自身情况的限制,会对人群疏散效率产生影响。姜传胜等 [23] 研究了残疾群体与健康群体在疏散过程中的相互影响,指出残疾人的存在很可能影响健康人群的疏散。然而,目前关于特殊人群疏散方面的理论探讨相对较少。
本文针对特殊人群中行动不便的行人,考虑其复杂的心理行为特征,建立了一般人群中含有行动不便行人时的元胞自动机模型。通过考虑行动不便行人的比例、位置分布等因素,对大厅内的行人疏散进行了数值模拟,分析、讨论了以上因素对人群疏散效率的影响,模拟结果对行人疏散,特别是高密度下行人的分流设计具有一定的指导意义。
2. 模型
模型如图1所示,将房间的尺寸
均匀划分为有限的二维网格,每个网格相当于一个元胞,元胞的尺寸大小为
[7] ,L表示房间的宽度,W表示房间的出口宽度。每个元胞或被一位行人占据,或为空。黑色部分为墙壁,绿色代表行动不便的行人,红色表示正常行人,出口位置为白色。
研究发现:行动不便行人如残疾人、老年人,相比正常行人,行动迟缓、步态缓慢、缺乏灵活性。
据此分析,采用摩尔(Moore)型邻居 [7] ,不考虑后退行为,正常行人和行动不便行人移动邻域分别如下:正常人在每个离散仿真时间步,可向摩尔(Moore)型邻居移动一个元胞的距离或者保持不动(图2(a));行动不便的人在每三个离散仿真时间步,可向摩尔(Moore)型邻居移动一个元胞的距离或者保持不动(图2(b))。
行人移动方向的选择由转移概率来确定。
假设(i,j)为行人的坐标,(i0,j0)为模型出口坐标,(x,y)为行人下一步移动坐标,行人(i,j)的移动邻域记为
,其中空元胞组成的集合记为
,则移动概率如下:
;(行人下一步移动位置不为空,则停在原位置)
;(行人下一步移动位置为空,则等概率选择方向移动)
。(行人在出口位置,则下一步一定移出系统),
表示
中元素个数。
模型更新规则如下:给定大厅内行人随机的初始分布;确定行人种类;根据不同行人各自的移动规则确定下一步移动目标,如果到达出口则移出系统;在此时间步内完成每位行人的位置更新;重复上述规则直到房间内的全部行人移出。
3. 模拟结果与讨论
初始时刻,行人以一定的密度随机地分布在系统中,并采用随机序列并行的方法按上述规则进行位置更新。数值模拟中,为了消除初始位置的随机性对结果的影响,系统的疏散时间T均为20个样本取平均的结果。如无特殊说明,参数设置如下:
,
,
,N为行人总数,定义行动不便行人所占比例为n,则
,M为行动不便行人总数。
首先研究行动不便行人所占比例对疏散时间的影响。图3给出了行动不便行人所占不同比例下混合人群疏散时间T与密度ρ之间的关系。可以看出,在不同密度范围内,行动不便行人比例对疏散时间的影响是不同的。在相同密度情况下,只要人群中有行动不便的行人,都会降低整个混合人群的疏散效率,且随着行动不便行人所占比例的增加,疏散时间亦显著增加。这是因为行动不便的人移动速度远低于正常人,并且其所能够选择的方向也少于正常人。在低密度情况下,由于行人较为稀少,人与人之间的碰撞等相互作用可以忽略不计,行动不便的人对正常人的移动造成的影响也可忽略,所以不同人群进行疏散所需要的时间相差不大。但是,随着人群密度的增大,行动不便行人所占比例对人群疏散时间的影响逐渐明显,在高密度下,不同人群进行疏散所需要的时间相差巨大。例如:人群密度0.8时,正常人群疏散时间约为200 s,在人群中只要有行动不便行人,这一疏散时间将显著增加,当特殊人群比例达到0.8时,疏散时间则翻倍,增加到400多秒,可见行动不便的人在移动过程中速度缓慢,会对正常人的移动造成障碍。随着数量的增加,过多行动不便的人聚集在一起,还影响了正常人的移动速度以及方向的选
 (a)
(a) (b)
(b)
Figure 2. The selectable movement directions. (a) Normal pedestrians; (b) Pedestrians who are unable to move freely
图2. 行人可选择的移动方向。(a) 正常行人;(b) 行动不便行人
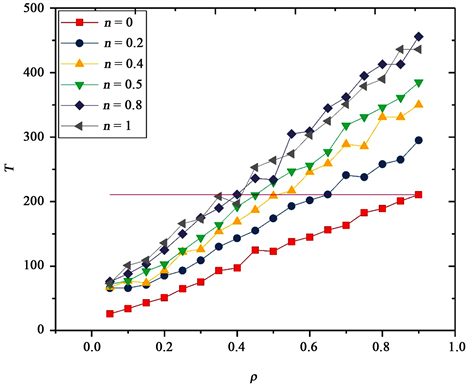
Figure 3. Relationship between evacuation time T and density ρ under n = 0, 0.2, 0.4, 0.5, 0.8, 1
图3. 行动不便行人比例n = 0,0.2,0.4,0.5,0.8,1下的疏散时间T与密度ρ的关系图
择,特别是当行动不便的人移动到出口,对正常人造成的影响更大。
为了更深入地研究行人疏散过程中的宏观行为现象,图4给出了高密度ρ = 0.7下不同行动不便行人比例时典型的时空演化状态斑图。在系统演化的初始阶段,行人均向着出口位置汇聚,并在出口形成拥堵瓶颈。全部为正常行人时,“成拱”现象更为明显,行人逐渐消散(见图4(a)~(c)所示),该情况相当于行人在出口位置依次逃离。当人群中有特殊行人时,行动不便的人会形成移动障碍,影响正常人的移动,空元胞数量及连续的空元胞明显增多,行人无法有效地利用可移动的空元胞(见图4(d)~(f)),造成疏散效率下降。全部为行动不便行人时,该现象更为显著(见图4(g)~(i))。以上结果表明,特殊人群的加入会对人群疏散过程中的宏观行为特征产生重要的影响。

Figure 4. The typical spatial-temporal patterns as ρ = 0.7. n = 0: (a) T = 40 s, (b) T = 100 s, (c) T = 190 s; n = 0.2: (d) T = 40 s, (e) T = 100 s, (f) T = 190 s; n = 1: (g) T = 40 s, (h) T = 100 s, (i) T = 190 s
图4. ρ = 0.7时,行人疏散过程中的时空演化状态斑图(n = 0: (a) T = 40 s, (b) T = 100 s, (c) T = 190 s; n = 0.2: (d) T = 40 s, (e) T = 100 s, (f) T = 190 s; n = 1: (g) T = 40 s, (h) T = 100 s, (i) T = 190 s)
为了更细致地探讨特殊人群的加入对行人宏观动力学特性的影响,图5给出了ρ = 0.7下,正常人群中加入3个行动不便行人时,行人疏散过程中的时空演化状态斑图。可以明显看出,在行动不便行人周围,存在大范围的空元胞区域,这一区域可视为“真空”区域,考虑到正常行人的心理作用,实际生活中主观上一般不会紧挨行动不便行人,从而造成客观上空间利用率的下降,最终导致疏散效率的下降。
最后探讨行动不便行人所处位置对疏散效率的影响。我们考虑了5种位置分布(见图6),分别为:case1代表行动不便行人在门口位置(即图6中A区域),case2代表在靠近出口的墙角位置(即图6中B区域),case3代表在房间的中间位置(即图6中C区域),case4代表在远离出口的墙角位置(即图6中D区域),case5代表随机分布。我们模拟了低、中、高三种密度下,行动不便行人比例为0.2时,人群疏散时间与行动不便行人5种不同的位置分布的关系图,如图7所示。可以看出:整体而言,中低高三种密度下,将行人置于出口附近,会提高疏散效率。低密度下,特殊人群置于出口附近,疏散时间显然最短,但中高密度下,这一优势被弱化,将行人置于整个房间的中央和行人在出口附近,所需的总的疏散时间基本相同,
 (a)
(a) (b)
(b)
Figure 5. The typical spatial-temporal patterns as ρ = 0.7. (a) T = 10 s; (b) T = 40 s
图5. ρ = 0.7时,行人疏散过程中的时空演化状态斑图。(a) T = 10 s;(b) T = 40 s

Figure 6. The distribution of pedestrians who are unable to move freely
图6. 行动不便行人位置分布区域示意图

Figure 7. Relationship between evacuation time T and case under n = 0.2, ρ = 0.1, 0.4, 0.7
图7. n = 0.2,ρ = 0.1,0.4,0.7时,疏散时间T与case的关系图
这说明随着人群密度的增加,出口附近的行动不便行人对房间内的其他行人形成了阻碍,已到达出口附近的正常行人也不能顺利通过门口。此外,中低密度下,5种位置分布下的疏散效率的变化趋势大致相同,相比随机分布,将特殊人群置于区域D所需要的疏散时间最长。高密度下,可以发现,行动不便行人随机分布时对应的疏散时间最长,不利于人群疏散,正如图5分析时指出的,每一个特殊行人周围都有可能出现多个空的元胞,空间利用率急剧下降。这种情况下,只要将特殊行人和正常行人分开,避免相互的干扰将有利于人群的疏散,特别是将行动不便行人置于出口附近或房间中央位置时,所对应的疏散时间最短,这说明当疏散开始时,若行动不便行人不能直接到达出口附近时,可适当引导这些行人先到房间中央,尽可能地避免干扰正常人群,为最优的疏散策略。
4. 结论
本文通过考虑人群中加入行动不便的人,建立了混合人群疏散的元胞自动机模型。数值模拟研究了行动不便行人的加入对疏散效率的影响,并重点探讨了人群密度、行人不便行人比例及位置分布等因素对房间内行人疏散过程的影响。通过对疏散时间及典型时空演化斑图的研究,我们得出以下结论:
1) 人群中加入行动不便行人将会影响行人总体的疏散时间。
2) 低密度下,行人不便行人对人群疏散效率影响不明显,随着密度的增加,行动不便行人所占比例的增大则会导致混合人群的疏散效率显著下降。
3) 高密度下,将行动不便行人和正常行人分开,会大幅提高疏散效率,且将行动不便行人置于出口附近或房间中央位置,对人群疏散最有利。
需要指出的是,本文仅研究了特殊人群中的行动不便行人,且主要考虑行动不便行人与正常行人的速度差异。在后续的研究中,我们将进一步完善模型,充分考虑行动不便行人的心理、行为因素及疏散场景的复杂性,如断电、场景内有障碍物等;此外,通过调研、实验等手段,获取实际环境中行人的信息来校正模型中参数,使模型能更好地反映和指导实际。
致谢
本论文获国家自然科学基金(11562020)、山西省自然科学基金(201601D011013)、山西省留学回国人员科技活动择优资助项目(2017004)资助。