房地产周期性波动的谱分析研究

Study on Spectral Analysis of Real Estate Cyclic Fluctuation

摘要: 简述研究具有周期特征的经济数据的理论工具，依据1988~2016年全国房地产市场供求类数据，提取主成分得到供求双方的综合指标；讨论综合指标时序值的稳定性特征，利用谱分析计算供求双方的周期。研究表明：全国房地产市场供求双方均呈现周期性波动；供给方存在3.5年的主周期和5.6年的次周期，需求方存在4.67年的主周期和2.8年的次周期；从长期发展来看，供求双方具有均衡发展的趋势。

Abstract: This paper first briefly describes the theoretical tools on studying economic data with periodic characteristics, then key indicators both of the supply and demand are identified by extracting the principal components from statistical data of real estate market in China from 1988 to 2016. Discussing the stability characteristics of the key indicators, the cycles both of the supply and demand is calculated by using spectral analysis techniques. The results show that both supply and demand fluctuate periodically. The supply has a main cycle about 3.5-year long and a secondary 5.6-year cycle. In the meantime, the demand has a main cycle of 4.67 and a sub-cycle of 2.8 years. From the long-term development, the supply and demand would have the trend of balanced development.

1. 引言

类似于自然现象具有周期性，房地产领域相关经济活动同样具有周期性 [1] [2] ，供给方与需求方在动态变化中相互作用；其他的处于动态变化中的各种经济活动也呈现出一定的周期性，例如在各类生产活动中，商品的生产从原材料的选取、加工、投入市场均有一定的生产周期。在商品的流通领域中，商品从生产、销售，再到消费者购买商品，同样具有一定的周期。研究 [3] [4] [5] [6] 表明，宏观经济与微观经济均具有一定的周期性。在研究宏观经济运行活动趋势方面，上世纪70年代之前，常用凯恩斯主义的经济周期理论对此作解释；20世纪80年代以后的二十多年中，占主导地位 [3] [4] 的是以真实经济周期理论(Real Business Cycle，RBC理论)为核心的新古典宏观经济理论。凯恩斯主义的经济周期理论将宏观经济周期分为短期波动和长期波动；约瑟夫·阿洛斯·熊彼特 [6] [7] 的“创新”理论，即经济发展理论，研究动态方式出现的经济活动中不断变化的各种趋势。熊彼特的“创新”理论，认为长、中、短三种周期是并存于各类经济活动之中。长周期是以首创者尼古拉·D·康德拉季耶夫命名，称为“康德拉季耶夫周期”，约为50年左右；中周期以最先提出者法国的克莱·尤格拉命名，称为“尤格拉周期”，平均约为9到10年；称为“基钦周期”的是短周期，由美国的约瑟夫·基钦提出的，平均40个月左右，约为3.3年。熊彼特认为，几乎每个经济活动中，这三种周期相互交织，同时存在。

经济活动中隐藏的内在周期特征，可以通过对经济活动中产生的大量数据做分析研究得到。最简洁的方式是直接对这些时间序列进行分析研究。时间序列数据中夹杂着各种扰动因素，通过时域上的分析，抽取其中的周期性成分可能有较大的难度，人们转而研究这些数据在频域上的变化情况。谱分析方法是频域上处理时间序列 [8] 的较好方法之一，该方法将数据分解成许多不同频率、不同相位和不同振幅的周期分量的叠加，通过寻找波峰得到主要的周期特征。经济活动或其他社会活动中产生的数据量庞大，各具特色，一般不能直接应用谱分析，需要对这些数据做规范化处理，分析它们是否具有共线性特点，给出反应数据特质的综合指标，即主成分 [9]。已有众多的研究工作者利用谱分析研究各类经济现象 [10] - [15]。曾峣 [10] 、张红 [11] 、李玉梅 [13] 等利用谱分析研究了房地产市场或房地产价格变动的周期。张红 [11] 等选用1992~2005年北京市房地产行业的供给方与需求方的统计数据，结合谱分析方法与主成分方法，研究得出北京市房地产行业供求关系基本均衡，存在为期3年的周期，但供给方还有一个为期7年的次周期。李玉梅 [13] 研究了我国房地产1998~2010年的季度数据，通过对房地产价格的分析，得出了价格波动具有为期3年或2年的周期，期间我国经济主周期为2.23年。

本文选取1988~2016年这一时间区间房地产行业供求双方的相关数据，数据来源于中国知网上相关年份的中国统计年鉴或房地产行业的统计年鉴。我们利用的供求双方的变量相似于张红 [10] 文中的供求因素，但略有不同，剔除了几个我们认为影响较弱的变量。在对供求双方数据进行规范化之后，提取双方数据的综合指标，进行谱分析研究，以确定该时间区间内供求双方的主周期和次周期长度，讨论双方的关联关系，希冀能提供一定的借鉴作用。后续内容中，首先介绍主成分分析法与谱分析方法的机理；接着进行实例分析，对数据进行规范化处理，给出综合指标，计算频率谱，分析周期性；最后给出我们的结论。

2. 数据处理的理论基础

谱分析处理随机过程中的时间序列数据时，一方面必须有足够的数据量，不少于200次的观测数据；另一方面要求时间序列具有平稳特征。谱分析的本质上是用离散傅立叶级数对时间序列进行拟合，有严谨的数学理论作依据。拟合的傅立叶级数若具有通用性，即不会因为不同时间段而产生较大的扰动性，就需要处理的随机过程具有平稳性，此时时间序列的数据在时间轴上表现为在均值附近上下波动，理论上的论证由单根检验完成。若时间序列本身不具有平稳特征，它的一阶差分或高阶差分必须满足平稳性要求。

考虑房地产行业的供给方与需求方均有多个因素组成，它们的计量单位不同，分析研究时先对数据做规范化处理，即转化为均值为0、标准差为1的数据；然后利用主成分分析法给出供给方和需求方的综合指标，综合指标要求保留了原来变量绝大部分信息。

2.1. 主成分分析法

主成分分析 [16] 的核心在于降维，将原有的多个性能指标(即多个自变量)减少为只含有少数几个综合性能指标。这些综合性能指标称为派生变量，是原来的性能指标的线性组合，它们相互独立且保留了原来变量绝大部分信息，这样的派生变量称之为主成分。

设x是有n个随机变量组成的列向量¹。主成分分析法中，寻找主成分的步骤如下²：

第一步 寻找第一个主成分，即找出x的一个线性组合 ${\beta }_1$ ，记为 ${\beta }_1\triangleq {\alpha }_1^{\text{T}}x$ ，其中 ${\alpha }_1={\left({\alpha }_{11},{\alpha }_{12},\cdots ,{\alpha }_{1n}\right)}^{\text{T}}$ 是一个n维列向量， $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$ ， $\mathrm{var}\left({\beta }_1\right)$ 为 ${\beta }_1$ 的方差。

${\beta }_1\triangleq {\alpha }_1^{\text{T}}x={\alpha }_{11}{x}_1+{\alpha }_{12}{x}_2+\cdots +{\alpha }_{1n}{x}_n$ ，

s.t. $\mathrm{var}\left({\beta }_1\right)$ 最大，且 ${\alpha }_1^{\text{T}}\cdot {\alpha }_1=1$ 。

第二步 寻找第二个主成分，也即寻找x的第二个线性组合 ${\beta }_2$ ，记为 ${\beta }_2\triangleq {\alpha }_2^{\text{T}}x$ ，其中 ${\alpha }_2={\left({\alpha }_{21},{\alpha }_{22},\cdots ,{\alpha }_{2n}\right)}^{\text{T}}$ 是一个n维列向量， $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$ ，

${\beta }_2\triangleq {\alpha }_2^{\text{T}}x={\alpha }_{21}{x}_1+{\alpha }_{22}{x}_2+\cdots +{\alpha }_{2n}{x}_n$ ，

s.t. $\mathrm{var}\left({\beta }_2\right)$ 最大，且 ${\alpha }_2^{\text{T}}\cdot {\alpha }_2=1$ ， ${\beta }_1$ 与 ${\beta }_2$ 线性无关

以此类推，直至找到线性关系 ${\beta }_k$ ，使其与 ${\beta }_1,{\beta }_2,\cdots ,{\beta }_{k-1}$ 不相关且具有最大方差。至此，k个主成分找到了。

利用数学推导过程可以证明，向量 ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_k$ 分别是随机变量向量x的协方差矩阵 $\sum$ 的特征向量，其特征值分别为 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k$ ，且 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k$ 是矩阵 $\sum$ 依大小次序排列的特征值，其中 ${\lambda }_1$ 最大特征值。

依据 $\frac{{\displaystyle \underset{i=1}{\overset{s}{\sum }}\left|{\lambda }_i\right|}}{{\displaystyle \underset{i=1}{\overset{t}{\sum }}\left|{\lambda }_i\right|}}\ge 95\%\text{or}90\%$ 确定从 $\sum$ 所有t个特征值 ${\lambda }_i\left(i=1,\cdots ,t\right)$ 中选取s个特征值 ${\lambda }_i\left(i=1,\cdots ,s\right)$ 和相应的特征向量，从而选取s个主成分。

2.2. 谱分析方法

谱分析方法是在频域上分析时间序列的一种有效而实用的方法，它将时间序列表示成不同振幅、不同频率的分量的叠加，即用傅立叶级数表示时间序列。谱分析应用必须满足两个条件：第一、不少于200次的理论观测数据，第二、时间序列具有平稳特征，即整个时间区间中时间序列的方差和均值保持不变；如果时间序列本身不满足平稳性，它的一阶或高阶差分序列具有静态性。

谱分析的机理 [10] 对于一个具有平稳性的时间序列 $X_t\left(t=1,2,\cdots ,N\right)$ ，通常可用傅立叶级数来拟合：

$X_t=A_0+{\displaystyle \underset{m=1}{\overset{n}{\sum }}\left(A_m\cos \left(2\text{π}mt/N\right)+B_m\sin \left(2\text{π}mt/N\right)\right)+{\epsilon }_t},t=1,2,\cdots ,N$ , (1)

其中：N为样本容量，且 $N=2n$ ； $t=1,2,\cdots ,N$ 为时间指数； $m=1,2,\cdots ,n$ ；频率 $\frac{1}{N}$ 为样本容量的倒数； $\frac{m}{N}$ 为第m次谐波的频率； ${\epsilon }_t$ 为随机误差项。

利用最小二乘法估计，得到傅立叶级数拟合方程(1)的系数，并代入式(1)，得

$\begin{array}{c}{X}_t=A_0+{\displaystyle \underset{m=1}{\overset{n}{\sum }}\{\left(\frac{2}{N}{\displaystyle \underset{t=1}{\overset{N}{\sum }}{X}_t\cos \left(2\text{π}mt/N\right)}\right)\cos \left(2\text{π}mt/N\right)}\\ +\left(\frac{2}{N}{\displaystyle \underset{t=1}{\overset{N}{\sum }}{X}_t\sin \left(2\text{π}mt/N\right)}\right)\sin \left(2\text{π}mt/N\right)\}+{\epsilon }_t\\ =A_0+2{\displaystyle \underset{m=1}{\overset{n}{\sum }}\{\left(\frac{1}{N}{\displaystyle \underset{t=1}{\overset{N}{\sum }}{X}_t\cos \left(2\text{π}mt/N\right)}\right)\cos \left(2\text{π}mt/N\right)}\\ +\left(\frac{1}{N}{\displaystyle \underset{t=1}{\overset{N}{\sum }}{X}_t\sin \left(2\text{π}mt/N\right)}\right)\sin \left(2\text{π}mt/N\right)\}+{\epsilon }_t\end{array}$

其中 $A_0=\frac{x_1+x_2+\cdots +x_N}{N}={\displaystyle \underset{t=1}{\overset{N}{\sum }}\frac{x_t}{N}}$ ；

所以傅立叶级数拟合方程的系数和 $X_t$ 的谱密度及周期长度分别可写成：

${\bar{A}}_m=\frac{1}{N}{\displaystyle \underset{t=1}{\overset{N}{\sum }}{X}_t\cos \left(2\text{π}mt/N\right)},m=1,2,\cdots ,n$ (2)

${\bar{B}}_m=\frac{1}{N}{\displaystyle \underset{t=1}{\overset{N}{\sum }}{X}_t\sin \left(2\text{π}mt/N\right)},m=1,2,\cdots ,n$ (3)

$I\left(f_m\right)=N\left({\bar{A}}_m^2+{\bar{B}}_m^2\right),m=1,2,\cdots ,n$ (4)

$周期长度=\max \left\{N\left({\bar{A}}_1^2+{\bar{B}}_1^2\right)\to N,N\left({\bar{A}}_2^2+{\bar{B}}_2^2\right)\to \frac{N}{2},\cdots ,N\left({\bar{A}}_n^2+{\bar{B}}_n^2\right)\to \frac{N}{n}\right\}$ .

3. 实证分析研究

根据1988~2016年房地产行业的相关数据,采用“主成分分析法”和“谱分析法”识别全国房地产市场周期。虽然观测的数据少于200个，但若将每年的数据划分成12个月，此时按月份的数据量就不少于200个，满足谱分析对数据量的要求。

3.1. 供给类与需求类指标选择

根据周期理论 [1] [2] ，供需变量选择见表1所示。

3.2. 供需双方数据及其规范化

从中国知网上中国统计年鉴或房地产行业的统计年鉴得到表2中的统计数据，对于这些数据进行规范化处理，使得每一列数据的均值为0，标准差为1，得到了标准化后的数据值(见表3)。

Table 1. Variables of both suppliers and demanders

表1. 供需双方指标

Table 2. Data of both supply and demand in real estate industry (1987-2016)

表2. 房地产行业供需双方数据(1987~2016)

Table 3. Standardized data of both supply and demand in real estate industry (1988-2016)

表3. 房地产行业供需双方标准化数据(1988~2016)

3.3. 主成分提取

对标准化的数据值按照供给类与需求类分别提取主成分，并绘制主成分的时序图。表4、表5分别列出了供给类提取的主成分及相关信息情况、需求类提取的主成分及相关信息情况(Prin1指第一主成分，其余类同)。

主成分的时序图见图1、图2所示，图中横坐标代表按年计的时间序号(1代表1988年,…,29代表2016年)，data1为主成分1，其余类同。

Table 4. From the Supply data: Eigenvalues and the corresponding principal components

表4. 供给类：特征值信息及相应的主成分

Table 5. From the Demand data: Eigenvalues and the corresponding principal components

表5. 需求类：特征值信息及相应的主成分

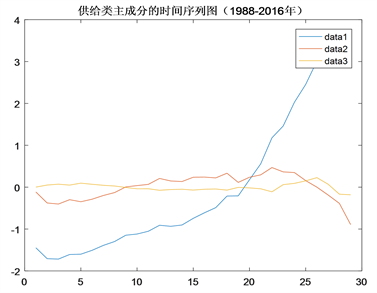
Figure 1. Time-series graphs of the supplies’ principal components

图1. 供给类主成分的时间序图

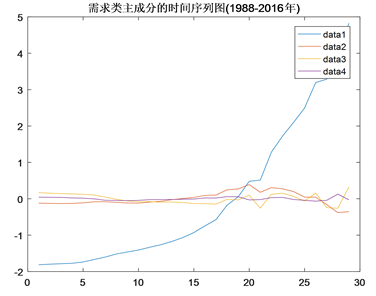
Figure 2. Time-series graphs of the demands’ principal components

图2. 需求类成分的时间序列图

3.4. 频率谱分析

考虑到供给类与需求类的第一主成分的贡献率分别为96.5577%、98.5368%，均超过95%，所以我们不妨选择各自的第一主成分作为供给类与需求类的综合指标值，并计算它们的一次差分与二次差分(见表6)。

绘制供需双方的综合指标、一阶差分及二阶差分时序图，如图3~5所示。各图中，横坐标代表按年计的时间序号(1代表1988年,…,29代表2016年)，data 1为供给类的数据，data 2为需求类的数据。观察图3~5，供需双方的二阶差分序列具有静态性，利用谱分析方法研究房地产行业的变动规律是可行的。

Table 6. Synthetical variable information of supply and demand

表6. 供需双方综合指标信息

Figure 3. Time-series graph of the synthetical viables of supply and demand

图3. 供给类与需求类综合指标时序图

Figure 4. First-order difference time-series graph of the synthetical viables of supply and demand

图4. 供给类与需求类综合指标一阶差分时序图

Figure 5. Second-order difference time-series graph of the synthetical viables of supply and demand

图5. 供给类与需求类综合指标二阶差分时序图

供给类综合类指标(yy)与需求类综合类指标(xx)具有正相关性，我们利用回归分析，得到

$yy=0.8481\ast xx,且\text{bint}=\left[0.\text{7997},0.\text{8965}\right],$

其中bint为系数b = 0.8481估计值的95%置信区间。绘制需求类与供给类综合指标关系图及其残差图(见图6，图7)。

供需双方的正相关性在2014年和2016年出现了较大的偏差，可能的因素有：虽然2014年3月份全国“两会”中对房地产调控提出“分类调控”的原则，但受2014年之前的限购政策的影响，房地产市场并没有像预期一样回暖，甚至于下滑的趋势不断加剧，购房者的观望情绪亦愈演愈烈，整个房地产市场笼罩在悲观的情绪中。2016年初，国家出台了多项房地产政策，降低首付、降低契税、第二套改善性住房契税优惠政策，使得购房者购房的门槛及成本再次降低，刺激了整体楼市的回暖。

分析供需双方综合指标的时序图、其一阶差分及二阶差分时序图，我们易判断出：供需双方的综合指标及其一阶差分均不具有平稳性特征，而二阶差分呈现出平稳性趋势，不过二次差分值的时序图后期波动性均比较大。我们可以分析供需双方综合类指标的二阶差分的频率谱，研究供给类与需求类的周期性特点(见表7)。按照式(2)、(3)、(4)计算谱密度值，绘制二次差分频率谱分布图(见图8)。

Figure 6. Relation of the synthetical viables of supply and demand

图6. 需求类与供给类综合指标关系图

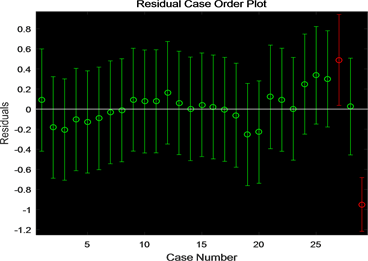
Figure 7. Residual case order plot on the relation of the synthetical viables of supply and demand

图7. 需求类与供给类综合指标关系的残差序列图

Figure 8. Second-order difference Spectral density Plot of synthetical viables on supply and demand

图 8. 供给类与需求类综合指标二次差分频谱分布图

观察供需双方的综合指标的二阶差分的谱密度的值及其分布图，显示出供给方的主谱峰、次谱峰分别发生在3.5年和5.6年，而需求方的主谱峰、次谱峰分别发生于4.67年和2.8年，然而，它们的谱密度的最大值、次最大值均分别位于2年和2.15年。

3.5. 周期性说明

谱密度分布图的谱峰，即曲线上凸起的拐点，对应的时间值即为相应的周期 [12]。观察供需双方的综合指标的二阶差分的密度谱图，我们了解到1988~2016年，全国房地产市场的供给类与需求类均存在主、次谱峰。因此，全国房地产市场供给方存在3.5年的主周期和5.6年的次周期；而需求方存在4.67年的主周期和2.8年的次周期。

然而，供需双方的综合指标的二阶差分的密度谱图显示，它们的谱密度的最大值、次最大值均分别位于2年和2.15年，这表明如果加以时日，再增加若干年的数据，可能得出供需双方存在不超过2年的主周期的结论。

4. 结论

1988~2016年全国房地产市场的供给类与需求类均具有明显的短周期的周期特征。我们给出的周期与张红 [11] 、李玉梅 [13] 等得出的主周期或次周期不完全一致，但相差不大，说明全国性房地产行业的供需周期与地方性房地产行业供需情况或价格波动联系比较紧密，我国1988~2016年房地产行业周期与1998~2010年我国经济主周期2.23也基本吻合。

全国房地产市场的供给方与需求方的主周期时间长度不一致，说明供给方与需求方的在一定程度存在不匹配的发展。但是，需求方的次周期的2倍等于供给方的次主周期，从长期发展来看，供给方与需求方具有均衡发展的趋势。

NOTES

¹这里的x已经标准化，即已中心化、均值化。

²尽管主成分分析没有忽略协方差和相关性，但是更注重方差。