1. 引言
在实际的控制理论中,对于众多类型性能指标的综合问题,控制必须采用状态反馈形式,文献 [1] [2] [3] 展示了在控制工程中一些对状态反馈的广泛应用。然而由于状态变量的内部变量属性决定了状态一般是不能直接测量的,从而状态反馈也是具有局限性的。在反馈的实现上,由系统输出的可量测属性所决定,输出反馈是在物理上可构成的,相应地,状态反馈则是在物理上不能构成的,因此,就反馈的物理实现而言,输出反馈要优越于状态反馈。文献 [4] [5] [6] 描述了动态输出反馈在控制工程中可靠控制的一些相关研究。然而可靠控制保守性强,浪费能源,所以本文的研究可以降低能源的浪费。在线性系统中,极点配置问题早已经在控制界进行了相当广泛的讨论。文献 [7] 介绍了区域极点配置问题的相关介绍。文献 [8] 给出了不确定系统动态输出反馈圆盘区域极点配置的充要条件。因此,输出反馈与极点配置问题的结合是有实际应用价值的,笔者以线性定常系统动态输出反馈圆盘区域极点配置为讨论基础也是具有实践性的。然而在控制工程中,控制系统往往会出现一些不确定因素,这些不确定因素会导致系统性能的降低,甚至失去稳定性,为了避免现实中的不足,容忍区间的研究进入了人们的视线中。文献 [9] [10] [11] [12] 描述了执行器增益偏差容忍区间及一些性能指标容忍区间的相关问题。容忍区间的概念在控制系统中的应用满足了系统的可靠性,为创建更好的控制系统提供了理论基础。上述所提文献虽然在系统出现扰动后,能采取一定的措施使系统依然保持某些较好的性能,但是会加大能源的浪费,本文弥补上述的不足,讨论了动态输出反馈容忍区间的概念,在保证系统维持优质性能的前提下,节约了大量的能源。
本文考虑动态输出反馈,完美地将输出反馈与圆盘区域极点配置结合,由于系统本身是具有一定的鲁棒性的,换言之若系统参数的波动没有使极点脱离指定区域,那么该系统的可靠性比较强,笔者研究的本质在于分析系统各参数的波动的范围,即参数波动使极点脱离指定区域的临界值,笔者把这个临界值取一定的范围叫做系统各不确定项的容忍区间。进一步,分析每个不确定项容忍区间的大小,研究出该参数波动对系统性能的影响程度,系统的设计人员可以参照每个参数的容忍区间的大小,来设计出具有理想性能的控制系统。最后通过数值仿真验证笔者所提的结论。
2. 问题描述
如下线性系统:
(1)
其中,
为系统的 维状态向量,
为系统的p维控制输入向量,
为系统的q维测量输出向量,A为系数矩阵,B为控制矩阵,C为系统的测量矩阵。
对于线性系统(1),设计动态输出反馈控制器:
(2)
由系统(1)和控制器(2)构成如下的闭环系统:
(3)
其中:
,
,
。这里
为待设计矩阵。
引理1 [13] :矩阵A的所有特征值均在半径为r,中心在
的圆盘中,当且仅当存在对称矩阵X,使得
(4)
引理2 [14] :对于系统(1),存在动态输出反馈控制器(2)使得闭环系统(3)的极点配置在以
为圆心,r为半径的圆盘区域内的充分必要条件是存在正定的矩阵
和矩阵
,使得线性矩阵不等式:
(5)
(6)
成立。动态输出反馈控制器的参数矩阵为:
(7)
其中矩阵M,N可由
确定。
为研究系统的不确定性范围,考虑线性系统的不确定参数,则该闭环系统为
(8)
其中:
,
,
。若系统(8)中第ij项上下波动时,则控制系统的单一不确定因素增益偏差模型是:
,其中
是第i行为1,剩余元素为0的列向量;
,
,
。
为阐述清晰,有如下符号表明:
1)
为矩阵A的特征值;
2)
为不确定因素第ij项波动时闭环系统的特征值;
3)
为
的实部值;
4)
为
的虚部值
定义:考虑控制系统的单一不确定因素增益偏差模型,存在
,
,若
使闭环系统(8)的极点持续保持在半径为r,圆心为
的圆盘中,那么称区间
为控制系统不确定参数波动的容忍区间。
3. 主要结果
定理:针对半径为r,圆心为
的圆盘区域极点配置问题,考虑闭环系统(8)的不确定区间
为该系统不确定参数容忍区间当且仅当:
,
为方程
的解。
其中:
,
,
,
,
,
,
,
,
;
。
证明:
1) 必要性
若闭环系统(8)的不确定区间
为该系统不确定参数的容忍区间,考虑线性系统第i项不确定参数波动时,该闭环系统的系数矩阵为
该特征值为
,取
,
,令
,设
为所有极点到圆心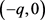 的最大距离,r为圆盘半径。若
的最大距离,r为圆盘半径。若 ,此时
,此时 ,即第 项不确定参数波动时,所有极点仍旧保持在圆盘内;若
,即第 项不确定参数波动时,所有极点仍旧保持在圆盘内;若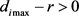 ,此时
,此时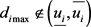 ,即该系统不确定参数波动时,部分极点已经脱离圆盘。若
,即该系统不确定参数波动时,部分极点已经脱离圆盘。若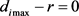 ,则一部分极点在圆盘的边界上,另一部分极点仍在圆盘内。由此可知若系统参数
,则一部分极点在圆盘的边界上,另一部分极点仍在圆盘内。由此可知若系统参数 在某值处向两侧不断扩展,则该系统极点到圆心的距离是不断增大的,所以当
在某值处向两侧不断扩展,则该系统极点到圆心的距离是不断增大的,所以当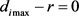 时,必会有两个解
时,必会有两个解 ,
, 。必要性得证。
。必要性得证。
2) 充分性
若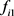 ,
, 为方程
为方程 的解。令
的解。令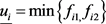 ,
,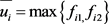 ,当
,当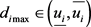 时,线性系统的所有极点均在圆盘内。若
时,线性系统的所有极点均在圆盘内。若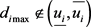 ,系统的部分或全部极点已经脱离圆盘,所以区间
,系统的部分或全部极点已经脱离圆盘,所以区间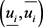 为圆盘区域极点配置问题中线性系统不确定参数第 项因素波动的容忍区间。定理由此得以证明。
为圆盘区域极点配置问题中线性系统不确定参数第 项因素波动的容忍区间。定理由此得以证明。
4. 仿真算例
飞机垂直翼的动态线性模型,其状态空间描述为:
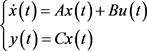
其中:
 ,
, ,
,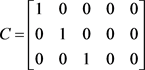
其中状态变量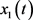 为飞行高度,
为飞行高度,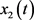 为前行速度,
为前行速度,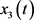 为倾斜角度,
为倾斜角度,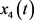 为倾斜速度,
为倾斜速度,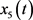 为垂直速度,控制输入
为垂直速度,控制输入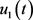 为阻流板角度,
为阻流板角度, 为前向加速度,
为前向加速度, 为升降舵角度,输出
为升降舵角度,输出 为飞行高度,
为飞行高度, 为前行速度,
为前行速度,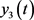 为倾斜角度。
为倾斜角度。
本文引用动态输出反馈,可以将飞机实例的输出量确切的提取出来,避免了状态反馈带来的不足。根据引理2可得:令线性系统极点配置到半径为r,圆心为 的圆盘区域中,如图1。图1描述的是将不稳定的线性系统极点配置到半径为r,圆心为
的圆盘区域中,如图1。图1描述的是将不稳定的线性系统极点配置到半径为r,圆心为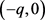 的圆盘区域中,该系统渐近稳定。
的圆盘区域中,该系统渐近稳定。
如下研究该线性系统中的不确定参数波动在圆盘区域中极点配置问题,定量此系统的第ij项不确定参数波动范围为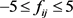 。并且研究系统在该不确定参数波动时容忍区间的问题。结果表明,线性系统不确定项的不同对该系统性能的影响程度也不同,容忍区间越小对系统性能的影响就越大。由于系统本身也具有一定的鲁棒性,可以看出即使是相同的参数波动范围,某个参数的波动也可以不影响系统的性能。如图2~4。
。并且研究系统在该不确定参数波动时容忍区间的问题。结果表明,线性系统不确定项的不同对该系统性能的影响程度也不同,容忍区间越小对系统性能的影响就越大。由于系统本身也具有一定的鲁棒性,可以看出即使是相同的参数波动范围,某个参数的波动也可以不影响系统的性能。如图2~4。

Figure 1. Pole distribution graph of pole disk region
图1. 圆盘区域极点分布图
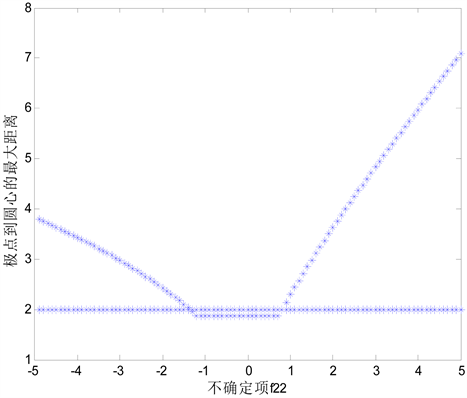
Figure 2. Tolerance interval of parameter f22
图2. 参数f22波动容忍区间

Figure 3. Tolerance interval of parameter f24
图3. 参数f24波动容忍区间
图2描述的是系统不确定参数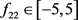 波动对系统性能的影响程度,可以观察到系统不确定参数f22波动容忍区间为
波动对系统性能的影响程度,可以观察到系统不确定参数f22波动容忍区间为 。图3描述的是系统不确定参数
。图3描述的是系统不确定参数 波动对系统性能的影响程度,可以观察到系统不确定参数f24波动容忍区间为
波动对系统性能的影响程度,可以观察到系统不确定参数f24波动容忍区间为 。图4描述的是系统不确定参数
。图4描述的是系统不确定参数 波动对系统性能的影响,可以观察到f12项自身具有很强的鲁棒性,不确定参数f12在范围
波动对系统性能的影响,可以观察到f12项自身具有很强的鲁棒性,不确定参数f12在范围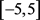 之间波动时对系统的性能是没有影响的,参数在该波动范围时极点始终在圆盘区域内。
之间波动时对系统的性能是没有影响的,参数在该波动范围时极点始终在圆盘区域内。

Figure 4. Tolerance interval of parameter f12
图4. 参数f12波动容忍区间
由上述分析可知,不确定参数f12项在该范围的波动下对系统性能是没有影响的,极点仍然保持在圆盘区域中。而f22项和f24项的鲁棒性较弱,在该范围的波动下极点已经脱离圆盘,f24的容忍区间比f22的大,对系统的影响较f22的影响小。系统设计人员可以利用本文结论参考各不确定项的容忍区间,设计理想的控制系统。
5. 结论
在控制系统中,系统本身是具有一定的鲁棒性的,即系统中各个参数的波动能使系统依然保持较好的性能。但是一旦系统中的不确定参数波动的过大,那么系统的鲁棒性是有限的,会使系统失去某些性能甚至是令系统不稳定。
本文将动态输出反馈与圆盘区域极点配置结合,在此基础上研究系统各个参数的波动范围,在波动范围内系统的极点依然能在圆盘区域内,在波动范围外极点就脱离了圆盘,从而确立了容忍区间的概念。通过建立系统的单一偏差模型,求得各个参数的容忍区间。加之对每个参数进行对比,会发现系统的不同参数其可靠性是不一致的。在设定的参数波动范围内,有的参数的波动会使极点脱离圆盘,通过对比容忍区间的大小可知,容忍区间越小,对系统的性能影响就越大,该参数就越不可靠。而在同样的参数波动范围内,部分参数对系统的性能没有影响,即该参数的鲁棒性较强。控制系统的设计人员可以参照本文的分析方法来设计其理想的控制系统。
基金项目
辽宁省科学技术基金项目(20170540823)。