1. 引言
机械设计与制造过程中往往会应用简易实用的四连杆机构,比如汽车发动机罩盖板与车身连接时,会利用四连杆机构控制其开启角度的大小。而为保证四连杆机构设计与安装的合理性与准确性,于设计早期发现并解决问题,进而缩短开发周期与费用,同步工程技术及虚拟仿真技术得到了广泛应用。由于不同车型的设计尺寸及要求千差万别,且同一组件在设计过程中往往会有多种备选方案,导致需要仿真的机构数量繁多,为应对大量资源的仿真,同一类型组件的标准化仿真方法显得非常重要。本文通过对车身与罩盖板连接处四连杆机构的运动学关系进行分析,并开发相应的函数辅助程序,得到了该类零件的一般仿真方法,为工程师们节约了仿真时间,保证了仿真的正确率。
2. 仿真软件中的四栏杆机构模型
四连杆机构的三维数字模型通过*.jt文件格式导入Tecnomatix中的Process Simulate仿真软件中,对其运动过程进行编辑与定义。
2.1. 建立运动杆件
Tecnomatix (Process Simulate)中共同运动的部件集合称为杆件,给四连杆添加运动学的时候首先将不同部件及其附加结构分割成相应杆件。如图1,该四连杆机构应用于发动机罩盖板与车身的连接位置,在开启罩盖板时负责其开启角度的控制及与车身的支撑。其工作原理为:固定杆与车身相连,盖板平台通过螺钉与发动机罩盖板相连,抬起罩盖板过程中前后两支撑杆随之转动,最小角度定位螺钉与最大角度定位台阶分别用来限制罩盖板掀起的最小与最大角度。本文分析过程中以杆件1为固定杆件,设置杆件4为驱动杆件,通过计算各杆连接部位转动轴的角度关系,得到四连杆机构的运动规律。
根据以上分析,在Tecnomatix (Process Simulate)中建立四个杆件,如表1所示。其中,Opening是为建立独立运动副而设置的空杆件。
 1-固定杆,2-前支撑杆,3-盖板平台,4-后支撑杆,5-最小角度定位螺钉,6-最大角度定位台阶
1-固定杆,2-前支撑杆,3-盖板平台,4-后支撑杆,5-最小角度定位螺钉,6-最大角度定位台阶
Figure 1. Structure of four-bar mechanism
图1. 四连杆机构的基本结构
2.2. 建立运动副
在Tecnomatix (Process Simulate)软件中为建立的杆件添加运动副和运动学(如图2),杆件设置成功后将被标示以不同的颜色,空杆件为灰。Tecnomatix (Process Simulate)中的运动副表达的是杆件间的相对运动,箭头由参照杆件指向运动杆件,运动杆件的轴线始终与参照杆件的运动状态相同。
四连杆机构共需要建立4个运动副,j1用来定义驱动杆件的转角范围及方向,j2~j4分别指的是两相连杆件之间的转动副,为非独立运动副,需要通过运动学分析定义运动函数,运动函数的大小为相对运动中,摆动角度相对于初始位置的变化量。
3. 四连杆机构的运动学分析
通过分析四连杆结构的运动数模模型,对机构各连杆的角度和长度数值创建运算公式。
3.1. 四连杆机构的机构类型
四连杆机构的转动模式如图3所示,在初始位置时连接杆保持水平。

Table 1. Link of four-bar mechanism
表1. 四连杆机构的杆件
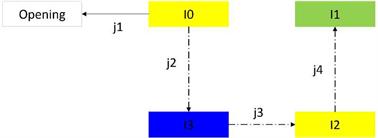
Figure 2. Kinematical pairs and link of four-bar mechanism
图2. 四连杆机构的杆件及运动副
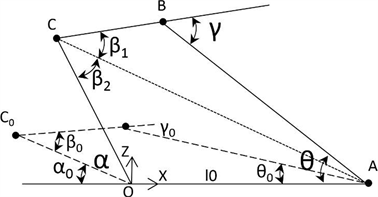
Figure 3. Revolute mode diagram of four-bar mechanism
图3. 四连杆机构转角示意图
3.2. 四连杆机构运动学分析
以驱动杆与不动杆连接轴轴心点O原点(如图3),以
方向为x轴,垂直于不动杆方向为z轴建立坐标系,四个铰链点的初始位置坐标分别为:
,相邻杆件间的初始夹角分别为
,经过转动后的夹角分别为
,其中θ为随动角度,当其余三个角度已确定时,该角度也将确定,因此不需进行计算。为计算简便,将β表示为如图3所示
两角之和。
分别为图示杆件的长度:
(1)
(2)
(3)
(4)
初始夹角
可分别表示为:
(5)
(6)
(7)
令经过转动后各相邻杆间的摆动角度分别为
则:
(8)
由三角形余弦定理可知:
(9)
即得:
(10)
如图3所示,新位置处C点坐标可表示为:
(11)
令此时点C至点A的连线距离为:
(12)
故可得:
(13)
4. 生成四连杆机构仿真运动函数的程序开发
4.1. 自定义运动副函数
Tecnomatix (Process Simulate)仿真软件对运动函数格式有严格要求,T表示转动副大小。由四连杆的运动关系,得到四连杆运动副的输入输出传递函数由分析可知j2的函数:
(14)
由式(9)得运动副j4的函数为:
(15)
由式(12)得运动副j3的函数为:
(16)
其中,
分别为四支杆件的长度,由所输入的初始坐标决定。
4.2. 基于VBA的仿真函数生成程序
由于建立3D四连杆机构数据的过程中对于四连杆运动学仿真的需求十分庞大,手动书写公式效率低且易出错,本文基于VBA开发了仿真函数生成程序,初始坐标输入部分及仿真函数生成部分截面分别如图4,图5所示。
在图4界面输入旋转点坐标值,程序获取用户输入的机构初始位置相关坐标后,将数值代入函数原

Figure 4. Original coordinate interface
图4. 初始坐标输入界面
型,以字符串格式输出至文本框,以j4的运动学函数为例,其函数原型为式(14),J4文本框的相应代码如下 [1] :

其中斜体为后台计算的数值量,其他(包括非斜体的括号)均为字符串格式,使用运算符&强制叠加后输出至界面,用户拷贝后至相应的函数定义窗口。
将生成的J2、J3、J4函数输入至图2对应的j2、j3、j4运动副中,四连杆机构运动关系即建立,可以在Tecnomatix仿真环境中模拟前盖铰链安装过程,验证产品工艺设计合理性。
5. 结束语
本文基于Tecnomatix (Process Simulate)建立了四连杆机构的运动学仿真,基本表达了四连杆机构的真实运动,基于VBA开发的仿真函数生成程序界面简洁,运行稳健可靠,节约了仿真工作时间,保证了正确率。本文亦可作为基于Tecnomatix (Process Simulate)的其他各类设备的运动学仿真的参考。